Synopsis

Keywords: Machine Learning/Artificial Intelligence, Diffusion/other diffusion imaging techniques

SDNet utilises the learning ability of deep neural networks with the robustness of model-based approaches to produce high quality fibre orientation distributions (FODs) from a reduced set of multi-shell diffusion weighted images (DWI). The cascaded architecture, with data consistency layers throughout, makes use of model based prior knowledge and spatial correlations within the DWI signal to achieve state-of-the-art performance in both sum of squared errors and angular correlation coefficient. Our model also shows competitive results with respect to apparent fibre density error and peak amplitude error over a range of regions of interest.

Introduction

Fibre Orientation Distributions (FODs) are widely utilised for both tractography and fibre specific, fixel-based analyses of diffusion-weighted brain imaging data. Accurate estimation of FODs can, however, require a large number of directions over multiple shells. As scan time increases linearly with the number of diffusion weighted images (DWIs), obtaining high quality FODs from reduced numbers of DWIs^1,2,3 would improve patient experience and reduce cost. In this work we propose Spherical Deconvolution Network (SDNet) to fully exploit prior knowledge of the model fitting algorithm, Constrained Spherical Deconvolution^4,5 (CSD), in conjunction with a powerful deep learning architecture.

Method

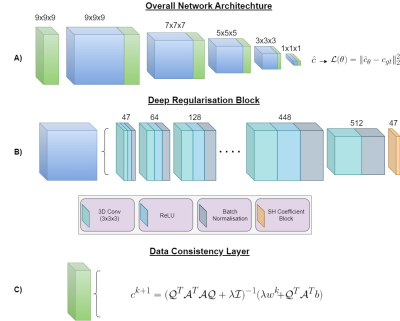
Spherical deconvolution (SD) can be posed as a typical minimisation problem,
$$c^* = \mathop {\arg \min }\limits_c { {\frac{1}{2m}\| {{\cal A} {\cal Q}c - {b}} \|_2^2} + {\cal R}\left( c \right)}.\text{ }(1)$$
where the objective function is the sum of a data consistency term, representing the forward spherical convolution process, and a regularisation term that conventionally includes a non-negativity constraint. In Eq.~(1), $$$c \in \mathbb{R}^{n}$$$ are the spherical harmonic coefficients representing the FOD, $$$b\in\mathbb{R}^{m}$$$ are the measured DWI signals, $$${\cal A} \in\mathbb{R}^{m \times n}$$$ describes the mapping from the spherical harmonic domain to the DWI domain, and $$${\cal Q} \in \mathbb{R}^{n \times n}$$$ are the rotational harmonics. By variable splitting, Eq.~(1) can be reformulated as a joint optimisation, solved using the following iterative, alternating optimisation scheme:
$$\left\{ \begin{array}{l}{c^{k + 1}} = \mathop {\arg \min }\limits_c \frac{1}{2m} \| {{\cal A} {\cal Q}c - {b}} \|_2^2 + \frac{\lambda }{2} \| c-w^{k} \|_2^2\\w^{k + 1} = \mathop {\arg \min }\limits_{{w}} {\frac{\lambda}{2}\| c^{k+1}-w \|_2^2} + {\cal R}\left( c \right) \\\end{array} \right.. \text{ }(2)$$
Our SDNet unrolls^6,7 the equations in Eq.~(2), and replaces the latter with a CNN with the goal of producing FODs similar to those fit to high angular resolution DWIs. The architecture of SDNet is depicted in Fig.~1. Note that $$$\lambda$$$ is a regularisation parameter, which can be optimised as a network parameter without manual tuning.

Experimental data:
Twenty subjects were randomly selected from the human connectome project (HCP⁸), split 10/3/7 into training, validation and testing, respectively. Each subject has 288 DWIs with b-values $$$0/1000/2000/3000 \text{ } s/mm^2 $$$ and 18/90/90/90 scans in each respective shell.

Data undersampling:
For each subject, 3/9/9/9 DWIs were selected, evenly spread over the three non-zero shells. Target FODs were fit to the fully sampled DWIs for each subject using the Multi-shell Multi-tissue (MSMT) CSD algorithm (MRtrix3⁹)

Performance analysis:
The accuracy of predicted SH coefficients was quantified by the angular correlation coefficient (ACC), sum of squared errors (SSE), peak amplitude error (PAE) and apparent fibre density error (AFDE).

Algorithm comparison:
SDNet was compared with FODNet, retrained on FODs fit using MSMT CSD. We also compared both methods to naive MSMT CSD applied to the undersampled data.

Region-of-interest selection:
The performance metrics were averaged over white matter, as well as three ROIs known to contain 1, 2 and 3 fixels:

• ROI 1: Corpus callosum
• ROI 2: Intersection of the middle cerebellar peduncle and cerebrospinal tract
• ROI 3: Intersection of the corpus callosum, cerebrospinal tract and superior longitudinal fascicle

Each region was limited to voxels containing the expected number of fixels in the ground truth FOD image. Tractseg¹⁰ was used to generate tract segmentation masks.

Results

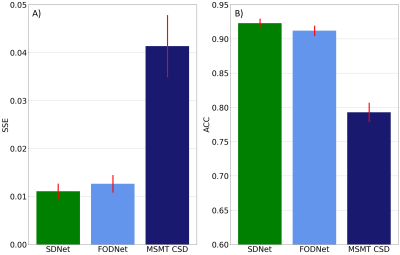
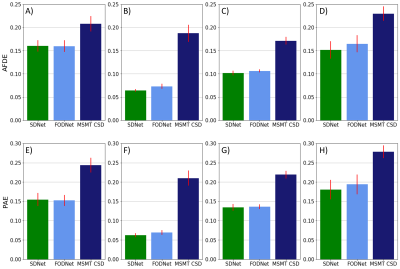
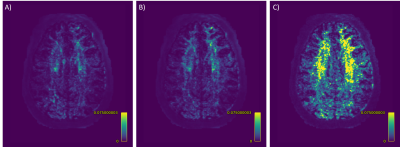
SDNet improved on FODNet with respect to SH accuracy (Fig.~3). SSE decreased from 0.0126 to 0.0111, a 12.0% decrease. The ACC increased from 0.9118 to 0.9228, a 1.2% increase. Fig.~4 shows that SDNet outperforms FODNet in ROIs 1 and 3. In ROI 1 the AFDE and PAE decrease by 0.0085 and 0.0068, corresponding to 11.6% and 9.84% decreases respectively. In ROI 3 the AFDE and PAE decrease by 0.0135 and 0.0133, corresponding to an 8.2% and 6.9% decrease, respectively. In all other ROIs, SDNet performs comparably with FODNet.

Discussion

SDNet can be applied to DWIs with different b-vectors to those used in training, since the matrix A can be adapted accordingly, and incorporates DWI signal information that is otherwise discarded by FODNet and other FOD super-resolution networks with such flexibility. This results in improved generalisability, and performance in reconstructing the SH coefficients, as reflected in Fig.~3. Furthermore, SDNet does not require FODs to be fit to the DWI's prior to applying the network.

Interestingly, we found that improvements in the reconstruction of SH coefficients, i.e. improved SSE and ACC, does not necessarily imply more accurately derived fixels. For both FODNet and SDNet, errors in AFDE and PAE were dominated by a failure to segment FODs into the correct number of fixels. In regions where fewer such errors occur, such as ROI 1, SDNet outperformed FODNet with respect to both PAE and AFDE. However, in other regions we observed that the aforementioned segmentation errors led to the two methods achieving similar performance. Recovering FODs which reduce the number of segmentation errors is an area we plan to explore in future work.

Conclusion

In this work we have proposed SDNet, a network that maintains the flexibility of FOD super-resolution networks, whilst incorporating model-based prior knowledge learned from the known DWI signal. We show that including such prior knowledge improves network performance over a range of metrics.