3786

Should We Harmonize or Denoise in Diffusion MRI?
Benjamin Ades-Aron1, Santiago Coelho1, Jelle Veraart1, Timothy M. Shepherd1, Dmitry S. Novikov1, and Els Fieremans1
1Radiology, Center for biomedical imaging, NYU Grossman School of Medicine, New York, NY, United States

Synopsis

Keywords: Data Processing, Diffusion/other diffusion imaging techniques, Harmonization Denoising

To address the ongoing reproducibility crisis in quantitative diffusion MRI (dMRI), efforts are underway to harmonize and improve precision of diffusion parameter estimation. Using inter- and intra-scanner test-retest higher order dMRI, we compare the reproducibility of two popular harmonization methods, ComBat and linear-RISH, to that of denoising using MPPCA on complex-valued dMRI. We find that denoising combined with harmonization improves voxel-wise test-retest ICC by up to 60% compared to harmonization alone. Using dMRI at different voxel sizes, we find that denoising reduces the bias due to varying noise floors more accurately than harmonization. Denoising appears essential to harmonize dMRI datasets.

Introduction

To make diffusion MRI (dMRI) truly quantitative and enable large-scale dMRI studies, there is a need to reliably combine data from multiple scanners, multiple sites and multiple protocols1,2. Unfortunately, variations associated with data acquired under different conditions manifest in varying levels of random noise and systematic bias that corrupt the diffusion parameter space3, reducing the sensitivity of dMRI measurements, concealing population-wise statistical effects, and preventing translation of quantitative diffusion to clinical practice.

Retrospective harmonization is a popular strategy to reduce systematic bias in data from differing sources, however, such techniques are agnostic to the underlying source of variation. In contrast, denoising methods are aimed at improving precision along with reducing noise floor induced bias by specifically modeling thermal noise (Fig. 1A).

Here, the effect of harmonization was compared to denoising by measuring their relative contribution to the repeatability of intra-scan, cross-scan, and cross-protocol test-retest comparisons and by evaluating bias due to varying voxel sizes (and noise floors). Harmonization was performed using widely-used ComBat4 or linear-RISH5,6, and denoising was performed using Marchenko-Pastur principal component analysis (MPPCA)7 on complex-valued dMRI data8.

Methods

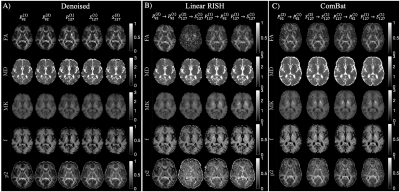
After informed consent, 30 healthy volunteers (15 female, age = 32.2±9.7 years) underwent brain dMRI on Siemens Magnetom Prisma and Skyra 3T systems. The diffusion acquisition parameters are shown in Figure 1B for two separate test-retest datasets: Protocol 1 for varying scanners and protocols; Protocol 2 for varying resolutions.

dMRI was preprocessed using either no denoising or MP-complex denoising. Then all data corrected for Gibbs ringing9 and eddy currents/EPI distortion/motion artifacts10,11 using DESIGNER12. Diffusion and kurtosis tensors were estimated using a weighted linear least squares3 to derive mean diffusivity (MD), fractional anisotropy (FA), mean kurtosis (MK), and white matter standard model parameters (f, p2) estimated with SMI toolbox13.

ComBat approaches harmonization using a statistical modeling approach, where multi-site parameters are independently adjusted based on linear regression. Diffusion parameters were warped to a central space using ANTs13 and ComBat was applied in paired batches for each comparison. Linear-RISH uses mean rotationally invariant spherical harmonic (RISH) features over a population to normalize those of an individual, and comparisons were performed in subject’s native space. All transformations were computed once and applied to all datasets to eliminate registration induced error.

In Protocol 1, test-retest variability was measured voxel-wise for each parameter for pairs of the five acquired datasets, where Prisma-1 ($$$P^{(1)}_{92}$$$) vs. Prisma-2 ($$$P^{(2)}_{92}$$$) and Skyra-1 ($$$S^{(1)}_{127}$$$) vs. Skyra-2 ($$$S^{(2)}_{127}$$$) measure scan-rescan variation (same scanner, identical TE), $$$P^{(1)}_{127}$$$ vs. $$$S^{(1)}_{127}$$$ measures inter-scan variation (varying scanner, identical TE), and $$$P^{(1)}_{92}$$$ vs $$$P^{(1)}_{127}$$$ measure inter-protocol variation (same scanner, different TE). Using the intra-class correlation coefficient (ICC) to measure voxel-wise one-to-one agreement in white matter, we compared harmonization without denoising, denoising alone, and using both harmonization and denoising. In Protocol 2, parameter values were extracted for test-retest data acquired at 1mm and 2mm isotropic resolution and compared in a similar setup.

Results

Figure 2 shows maps of MD, MK, f, and p2, demonstrating qualitative differences denoising and/or harmonization invoke on parameters.

Figure 3 shows scatter plots for parameters in all voxels of the posterior limb of the internal capsule (PLIC) for 20 subjects with intra-scanner (Prisma) test-retest.

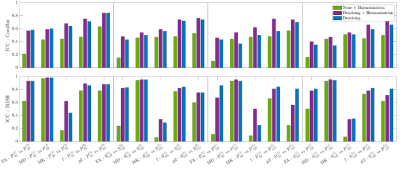
Figure 4 shows ICCs between each test-retest comparison for data processed with denoising and/or harmonization. Across all 40 comparisons (2 intra-scanner, 1 cross-scanner, 1 cross-protocol X 5 diffusion parameters), ICC based on harmonization alone is the lowest for 39/40 comparisons, corroborating the overall benefit of denoising prior to harmonization. ComBat+denoising results in a small yet consistent improvement of ICC, particularly for the cross-protocol comparison, while benefit of linear-RISH+denoising compared to just denoising is observed only for MK.

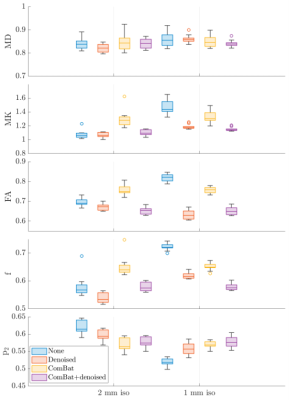
Figure 5 shows the effect of ComBat and/or denoising on reducing noise induced bias due to varying resolution. ComBat harmonization increased the amount of bias in low-resolution data to better match the level of bias in the high-res, low SNR dataset.

Discussion

We demonstrate that MP-complex denoising provides an essential component of harmonization to improve test-retest reproducibility of dMRI studies – e.g. there was 60% improvement in FA ICC when denoising compared to linear-RISH alone. This increased precision is most important when analyzing data using voxel-wise methods. ComBat results in a small yet consistent improvement of reproducibility, particularly for the cross-TE comparison. Testing the effect of harmonization on data with differing resolutions, we observed that ComBat increased the bias in low-resolution data to better match that of the high-resolution, highlighting the latent danger of agnostic harmonization. If bias comes from a known source (noise floor), it should be corrected using a targeted approach, therefore it is important to save complex-valued data and plan for bias reduction prior to acquisition. The observed effects of harmonization on parameter precision are dependent on the acquired protocols, and we would likely observe a greater effect for larger differences in scan settings, for comparisons over ROIs, or for data from different MRI vendors.

Conclusion

Should we harmonize or denoise dMRI data prior to parameter estimation? MP-complex8 denoising appears more effective than commonly employed harmonization methods to reduce known biases and maximize precision. Harmonization may provide additional marginal benefit and/or serve as a last resort to eliminate measurement-specific confounding effects.

Acknowledgements

This work was supported by NIH R21 NS081230 and R01 NS088040 and was performed at the Center of Advanced Imaging Innovation and Research, an NIBIB Biomedical Technology Resource Center (NIH P41 EB017183).

References

  1. Tax, C. M. et al. Cross-scanner and cross-protocol diffusion MRI data harmonisation: A benchmark database and evaluation of algorithms. NeuroImage 195, 285-299 (2019).
  2. Grech‐Sollars, M. et al. Multi‐centre reproducibility of diffusion MRI parameters for clinical sequences in the brain. NMR in Biomedicine 28, 468-485 (2015).
  3. Veraart, J., Sijbers, J., Sunaert, S., Leemans, A. & Jeurissen, B. Weighted linear least squares estimation of diffusion MRI parameters: strengths, limitations, and pitfalls. Neuroimage 81, 335-346 (2013).
  4. Fortin, J.-P. et al. Harmonization of multi-site diffusion tensor imaging data. Neuroimage 161, 149-170 (2017).
  5. Mirzaalian, H. et al. Inter-site and inter-scanner diffusion MRI data harmonization. NeuroImage 135, 311-323 (2016).
  6. Ning, L. et al. Cross-scanner and cross-protocol multi-shell diffusion MRI data harmonization: Algorithms and results. Neuroimage 221, 117128 (2020).
  7. Veraart, J. et al. Denoising of diffusion MRI using random matrix theory. Neuroimage 142, 394-406 (2016).
  8. Ades-Aron, B. et al. in In Proc ISMRM (Vol. 2105).
  9. Lee, H. H., Novikov, D. S. & Fieremans, E. Removal of partial Fourier‐induced Gibbs (RPG) ringing artifacts in MRI. Magnetic Resonance in Medicine 86, 2733-2750 (2021).
  10. Andersson, J. L., Skare, S. & Ashburner, J. How to correct susceptibility distortions in spin-echo echo-planar images: application to diffusion tensor imaging. Neuroimage 20, 870-888 (2003).
  11. Andersson, J. L. & Sotiropoulos, S. N. An integrated approach to correction for off-resonance effects and subject movement in diffusion MR imaging. Neuroimage 125, 1063-1078 (2016).
  12. Ades-Aron, B. et al. Evaluation of the accuracy and precision of the diffusion parameter EStImation with Gibbs and NoisE removal pipeline. Neuroimage 183, 532-543 (2018).
  13. Coelho, S. et al. (2022). Reproducibility of the Standard Model of diffusion in white matter on clinical MRI systems. NeuroImage, 257, 119290.
  14. Avants, B. B. et al. The Insight ToolKit image registration framework. Frontiers in neuroinformatics 8, 44 (2014).

Figures

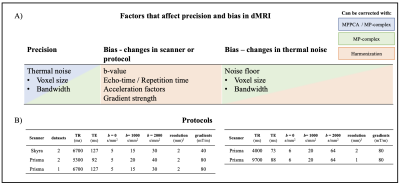
A) Potential sources of variability affecting parameter precision or bias. Magnitude denoising (blue) improves precision, denoising of complex-valued data (green) also corrects noise induced bias. Harmonization (red) attempts to correct for all sources of bias. B) Protocols used: Protocol 1 (left): 20 subjects scanned to acquire five datasets each, test-retest on the Prisma, test-retest on the Skyra, and one dataset on the Prisma with protocol matched to Skyra. Protocol 2 (right): 10 subjects scanned on the same scanner at two resolutions.


A) Qualitative demonstration of denoising or harmonization on DTI, DKI, and SMI measures (FA, MD, MK, f, and p2) across scan-rescan data on Prisma and Skyra scanners. A) MP-complex denoising; B) linear-RISH harmonization - notably FA and p2 maps are particularly corrupted by noise. C) ComBat harmonization– bias correction is evident in MK and f maps.

Comparison of harmonization and/or denoising on within-scanner test-retest data ($$$P^{(1)}_{92}$$$ vs $$$P^{(2)}_{92}$$$. Voxel-wise scatter plots pooled over white matter (PLIC) for all 20 subjects after nonlinear registration to a central space. Interclass correlation coefficients are shown on the upper left corner of each plot. Top row shows ComBat harmonization within-scan variability and bottom shows linear RISH harmonization. We note differences for denoising in the two comparisons, because the RISH is done in native space eliminating effects of registration.

Intraclass correlation coefficients for over four comparisons: within-scan variability ($$$P^{(1)}_{92}$$$ vs $$$P^{(2)}_{92}$$$ and $$$S^{(1)}_{127}$$$ vs $$$S^{(2)}_{127}$$$), Cross-protocol variability ($$$P^{(1)}_{92}$$$ vs $$$P^{(1)}_{127}$$$), and cross-scanner variability ($$$P^{(1)}_{127}$$$ vs $$$S^{(1)}_{127}$$$). We note ICCs are slightly lower for denoising in the Combat comparison (top row) as opposed to the linear-RISH comparison (bottom row), because the latter is done in native space eliminating the effect of registration, and lowering ICC.

Boxplots over 10 subjects from Protocol 2, showing ROI means in PLIC. No denoising, denoising, ComBat harmonization, and ComBat+denoising are compared across 1mm and 2mm isotropic resolution to compare the effect of harmonization at reducing the Rician noise floor. In contrast to denoising, ComBat introduces an unphysical bias, as FA values increase in 2mm data after harmonization to non-denoised 1mm data.

Proc. Intl. Soc. Mag. Reson. Med. 31 (2023)
3786
DOI: https://doi.org/10.58530/2023/3786