3783
tDKI-Net: a joint q-t space learning network for diffusion-time-dependent kurtosis imaging and Karger’s model fitting
Tianshu Zheng1, Ruicheng Ba1, Xiaoli Wang2, Xizhen Wang3, Chuyang Ye4, and Dan Wu1
1Department of Biomedical Engineering, College of Biomedical Engineering & Instrument Science, Zhejiang University, Hangzhou, Zhejiang, China, Hangzhou, China, 2School of Medical Imaging, Weifang Medical University, Weifang, Shandong, China, Weifang, China, 3Medical imaging center, Affiliated hospital of Weifang Medical University, Weifang, Shandong, China, Weifang, China, 4School of Integrated Circuits and Electronics, Beijing Institute of Technology, Beijing, China, Beijing, China
1Department of Biomedical Engineering, College of Biomedical Engineering & Instrument Science, Zhejiang University, Hangzhou, Zhejiang, China, Hangzhou, China, 2School of Medical Imaging, Weifang Medical University, Weifang, Shandong, China, Weifang, China, 3Medical imaging center, Affiliated hospital of Weifang Medical University, Weifang, Shandong, China, Weifang, China, 4School of Integrated Circuits and Electronics, Beijing Institute of Technology, Beijing, China, Beijing, China
Synopsis
Keywords: Machine Learning/Artificial Intelligence, Diffusion/other diffusion imaging techniques
Time-dependent diffusion magnetic resonance imaging (TDDMRI) is useful for non-invasive characterization of tissue microstructure. The TDDMRI models require both densely sampled q-space (b-value and diffusion direction) and t-space (diffusion time) data for microstructural fitting, leading to very time-consuming acquisition protocols. In this work, we presented a tDKI-Net to estimate diffusion kurtosis at multiple diffusion times, which was fed into the Karger model to obtain K0 and transmembrane exchange time, using downsampled q-space and t-space data. We tested the proposed network in the normal rat brains, as well as those in a rat model of Middle Cerebral Artery Occlusion.Introduction
Diffusion magnetic resonance imaging (dMRI) is a well-established neuroimaging technique for probing tissue microstructures1. Time-dependent dMRI (TDDMRI) captures microstructural size and transmembrane exchange by measuring the diffusivity or kurtosis at varying diffusion-times (td)2. Previous studies used a two-compartment Karger model3 to estimate cell-interstitial water exchange time ($$$\tau _{m}$$$) based on td-dependent diffusion kurtosis, here we will name it tDKI.For the tDKI model, we did not only need to densely sample the q-space (b-values and diffusion directions) to calculate DKI model but also need to densely sample the t-space to obtain the td-dependency. Thus, tDKI requires a time-consuming acquisition protocol, which is difficult for clinical translation.
In this work, we developed a tDKI-Net for simultaneous q-space learning of kurtosis and t-space learning of $$$\tau_{m}$$$. Moreover, we performed joint downsampling from q-space and t-space for b-value, gradient, and td for the first time. The network performance was tested in both normal and injured rat brains.
Methods
tDKI-Net (Fig. 1(a)) can be divided into two parts: the q-space learning network and the t-space learning network.Sparse Coding: We extended our previous approach on q-space sparse representation4–7 to t-space to fit kurtosis at individual td:
$$y={\Phi}x+{\eta}(1)$$
where, $$$y\in\mathbb{R}^{M}$$$ is the diffusion kurtosis in the t-space; $$${\Phi}\in\mathbb{R}^{M\times P}$$$ with M being the number of td and P being the size of the dictionary; $$$x$$$ is the sparse coefficient vector, and $$$\eta$$$ is the noise vector. The sparse representation of the diffusion signal $$$y$$$ can be obtained from minimizing the function as:
$$\boldsymbol{\min _{x}\left\|y-\Phi x\right\|_{2}^{2}}+\beta\boldsymbol{\|x\|_{1}}(2)$$
Where $$$\beta$$$ is a constant and controls the sparsity of $$$x$$$.
q-Space learning network: Due to the superior performance of extragradient (EG)-Unit in the q-space learning5, here, we chose EG-Unit as the q-Encoder to encode the signal in q-space at various td (Fig. 1(b)). The q-space networks were shown in the blue dashed rectangles, and more details can be found in [5].
t-Space learning network: We also adopted the EG-based network[5], [8] as t-Encoder shown in Fig. 1(c). The objective function has been proposed in Eq.(2) and it can be resolved as follows:
$$\mathbf{X}^{n+\frac{1}{2}}=H_{M}(\mathbf{X}^{n}+\mathbf{\Phi}_{\mathrm{1}} \mathbf{Y} -{\mathbf{\Phi}^{\mathrm{T}}_{1}} \mathbf{\Phi}_{\mathrm{1}} \mathbf{X}^{n} ) (3)$$
$$ \mathbf{X}^{n+1}=H_{M}(\mathbf{X}^{n}+\mathbf{\Phi}_{\mathrm{2}} \mathbf{Y} -{\mathbf{\Phi}^{\mathrm{T}}_{2}} \mathbf{\Phi}_{\mathrm{2}} \mathbf{X}^{n+\frac{1}{2} } ) (4)$$
Where, $$$H_{M}$$$ denotes a nonlinear operator:
$$H_{M}\left(\mathbf{X}_{i j}\right)= \begin{cases}0, & \text { if } \mathbf{X}_{i j}<\lambda \\ \mathbf{X}_{i j}, & \text { if } \mathbf{X}_{i j} \geq \lambda\end{cases}\ (5)$$
As none of the parameters in the iteration process is predetermined, Eq.(3) and (4) can be simplified as follows:
$$\mathbf{X}^{n+\frac{1}{2}}=H_{M}(\mathbf{S}^{1} \mathbf{X}^{n}+\mathbf{W}^{\mathrm{1}} \mathbf{Y}) (6)$$
$$\mathbf{X}^{n+\frac{1}{2}}=H_{M}(\mathbf{X}^{n} +\mathbf{W}^{\mathrm{1}} \mathbf{W}^{\mathrm{2}} \mathbf{Y} + \mathbf{S}^{2} \mathbf{X}^{n+\frac{1}{2} }) (7)$$
Where, $$$\mathbf{S}^{1}$$$,$$$\mathbf{S}^{2}$$$,$$$\mathbf{W}^{1}$$$, and $$$\mathbf{W}^{2}$$$ are learnable weights through the network.
Materials: dMRI was collected using a 7T Bruker scanner from 3 normal rats and 10 rats that underwent a model of transient Middle Cerebral Artery Occlusion (MCAO). Diffusion gradients were applied in 18 directions per b-value with 6 td (20, 50, 80, 100, 150, and 200 ms) at 3 b-values of 0.8, 1.5, and 2.5 ms/μm2 with the following acquisition parameters: repetition time/echo time = 2207/18 ms, in-plane resolution = 0.3×0.3 mm2, 10 slices with a slice thickness of 1 mm.
In order to get the gold standard, the DKE toolbox9 was used to get the kurtosis at different td with the fully sampled q-space, and then a Bayesian method modified from Gustafsson et al.10 was used to estimate the $$$K_{0}$$$ and $$$\tau_{m}$$$ from fully sampled t-space. The dataset was downsampled with randomly selected 9 gradients for b = 0.8 and 1.5 ms/μm2 in 4 td (20, 50, 100, and 200 ms).
Results
tDKI-Net of the normal rat brains: We first compared our method with an optimization-based approach using DKE toolbox and a learning-based network q-DL in estimating kurtosis with the downsampled q-space data (Fig. 2 (a)) on a normal rat. tDKI-Net achieved better results than DKE and q-DL in terms of the red arrow noted, which is a low signal area in the gold standard but high in DKE and q-DL. Then, we compared tDKI-Net with a Bayesian method and q-DL for Karger model fitting (Fig. 2(b)). Our proposed method kept the highest fidelity with the ground truth (red arrows in Fig. 2(b)) and least fitting error in both $$$K_{0}$$$ and $$$\tau_{m}$$$. The performance was compared quantitatively using mean square error (MSE) on the validation set in Table 1.tDKI-Net of MCAO-injured rat brains: In MCAO rats, similar results can be observed. tDKI-Net better preserved the injury information, especially at the long td, e.g., the elevated kurtosis at 150 ms (red arrow in Fig. 3). The improvement was more evident in the Karger’s fitted parameters, e.g., only tDKI-Net can capture the brain injury in $$$\frac{1}{\tau_{m}}$$$ map (red arrow in Fig. 3) with the downsampled data. Table 1 showed the fitting errors of were 12% lower than q-DL in MACO data ).
Discussion and Conclusion
In this work, we proposed a tDKI-Net for joint q-t space model fitting with downsampled data for the first time. Compared with other works, the model-based tDKI-Net achieved the lowest estimation error and the highest fidelity with the ground truth in both normal and injured brain tissues. We will generalize this tDKI-Net in the future so that it can be extended to more TDDMRI models and more clinical applications.Acknowledgements
This work is supported by Ministry of Science and Technology of the People’s Republic of China (2018YFE0114600, 2021ZD0200202), National Natural Science Foundation of China (61801424, 81971606, 82122032), and Science and Technology Department of Zhejiang Province (202006140, 2022C03057).References
[1] Mori S, Zhang J. Principles of Diffusion Tensor Imaging and Its Applications to Basic Neuroscience Research. Neuron 2006;51:527–539 doi: 10.1016/j.neuron.2006.08.012.[2] Jiang X, Li H, Xie J, Zhao P, Gore JC, Xu J. Quantification of cell size using temporal diffusion spectroscopy. Magn. Reson. Med. 2016;75:1076–1085 doi: 10.1002/mrm.25684.
[3] Solomon E, Lemberskiy G, Baete S, et al. Time-dependent diffusivity and kurtosis in phantoms and patients with head and neck cancer. Magn. Reson. Med. 2022:1–15 doi: 10.1002/mrm.29457.
[4] Zheng T, Sun C, Wang G, et al. A Model-driven Deep Learning Method Based on Sparse Coding to Accelerate IVIM Imaging in Fetal Brain. In: ISMRM 2021: The 29th International Society for Magnetic Resonance in Medicine. ; 2021.
[5] Zheng T, Zheng W, Sun Y, Zhang Y, Ye C, Wu D. An Adaptive Network with Extragradient for Diffusion MRI-Based Microstructure Estimation. In: International Conference on Medical Image Computing and Computer-Assisted Intervention. ; 2022.
[6] Zheng T, Hsu Y-C, Sun Y, Zhang Y, Ye C, Wu D. A Microstructural Estimation Transformer with Sparse Coding for NODDI (METSCN). In: ISMRM 2022: The 30th International Society for Magnetic Resonance in Medicine. ; 2022.
[7] Zheng T, Sun C, Zheng W, et al. A microstructure estimation Transformer inspired by sparse representation for diffusion MRI. arXiv Prepr. arXiv2205.06450 2022.
[8] Kong L, Sun W, Shang F, Liu Y, Liu H. Learned Interpretable Residual Extragradient ISTA for Sparse Coding. 2021.
[9] Tabesh A, Jensen JH, Ardekani BA, Helpern JA. Estimation of tensors and tensor-derived measures in diffusional kurtosis imaging. Magn. Reson. Med. 2011;65:823–836 doi: 10.1002/mrm.22655.
[10] Gustafsson O, Montelius M, Starck G, Ljungberg M. Impact of prior distributions and central tendency measures on Bayesian intravoxel incoherent motion model fitting. Magn. Reson. Med. 2018;79:1674–1683 doi: 10.1002/mrm.26783.
Figures
Fig. 1(a) The overall structure of tDKI-Net. Yns are diffusion signals collected at different td; q-Encoders are the q-space sparse representation units shown in Fig. 1(b); Iq is the number of iteration blocks. Mappings consist of fully connected layers mapping the encoded signal to the kurtosis at the corresponding td, respectively. The t-Encoder is the t-space sparse representation unit shown in Fig. 1(c) and It is the number of iteration blocks. (b) The q-Encoder unit used for the q-space sparse representation. (c) The t-Encoder unit used for the t-space sparse representation.
Fig. 2 (a)
The gold standard and estimated kurtosis at four diffusion-times based on DKE, q-DL, and tDKI-Net (ours) were compared in a normal rat brain with downsampled q-space data. (b) The gold standard, estimated, and estimation errors of Karger
parameters, based on Bayesian, q-DL,
and tDKI-Net (ours), were compared in
a normal rat brain with jointly downsampled q-t
space data.
Fig. 3 (a)
The gold standard and estimated kurtosis based
on DKE, q-DL, and tDKI-Net (ours) were compared in a
stroke test subject with q-t space downsampled. (b) The gold standard, estimated, and
estimation errors of Karger parameters, based on Bayesian, q-DL, and tDKI-Net (ours),
compared in a MCAO rat brain with joint downsampling.
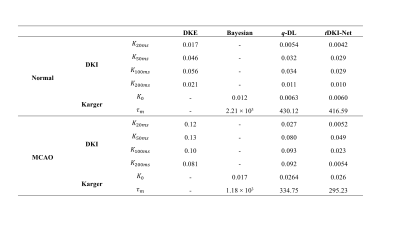
Table 1 Validation loss (MSE) of different algorithms
compared in DKI fitting (DKE, q-DL, tDKI-Net) and Karger fitting (Bayesian, q-DL, tDKI-Net)
DOI: https://doi.org/10.58530/2023/3783