INTRODUCTION

Nasopharyngeal carcinoma (NPC) is an epithelial cancer originating from the inner mucosa of the nasopharynx ¹, which is most commonly seen in men and has a high incidence mainly in southern China, Southeast Asia and North Africa. Patients with early detection and diagnosis of NPC disease have a higher 10-year survival rate, while the median survival of patients with advanced disease is only 3 years ². Therefore, correct diagnosis plays a crucial role in reducing mortality from NPC. Dynamic contrast-enhanced magnetic resonance imaging (DCE-MRI) is a functional noninvasive imaging modality. Researchers can obtain information about the physiological characteristics of tissue from DCE-MRI for tumor diagnosis. Among the features extracted from DCE-MRI using pharmacokinetics are the volume transfer constant (K_trans). As the blood vessels in the NPC region are rapidly generated, the vessel walls are weaker and more permeable, allowing for significantly faster diffusion of contrast from the interior of the new vessels into the tissue interstitium. K_trans represents the process of contrast transfer from the vessels to the tissue interstitium, i.e., contrast uptake. The description of the K_trans characteristics shows that there is a difference between K_trans in tumor areas and K_trans in nontumor areas. Therefore, this study explores the use of K_trans as modal information to assist in the segmentation of nasopharyngeal tumors.

METHODS

This prospective study acquired DCE-MRI data from 96 patients on a Siemens 3.0T MRI instrument. Thirty-five phases of DCE-MRI were acquired for each patient. The time-signal intensity curve (TIC) for each patient was drawn from the 35-phase data. The TIC was then converted to a tissue contrast concentration transformation curve according to equation (1.1) ³ and equation (1.2) ⁴.
$${{S{I_{post}}(t)} \over {S{I_{pre}}}} = {{1 - {e^{ - {{TR} \over {{T_{1post(t)}}}}}}} \over {1 - {e^{ - {{TR} \over {{T_{1pre}}}}}}}}, （1.1）$$

$${1 \over {{T_{1post(t)}}}} = {1 \over {{T_{1pre}}}} + {r_1}{C_t}, （1.2）$$

where SI_pre is the initial signal intensity, SI_post(t) is the signal intensity over time, T_1pre is the relaxation time of the initial trial, T_1post(t) is the relaxation time over time and TR is the repetition time (msec). C_t is the tissue contrast concentration, and r₁ (mM^-1s^-1) is the longitudinal contrast agent relaxation factor, which depends on the temperature, field strength and chemical structure of the contrast agent. In this study, the extended Tofts and Kermode (ETK) model was used to fit tissue contrast concentration profiles and to derive point-by-point K_trans values for DCE-MRI. The calculation formula is shown in equation (1.3).
$${C_t}(t) = {v_p}{C_p}(t) + {K_{{\mathop{\rm t}\nolimits} rans}}\int_0^t {{C_p}(t')} {e^{ - (({K_{trans}}/{v_e})(t - t'))}}dt', （1.3）$$

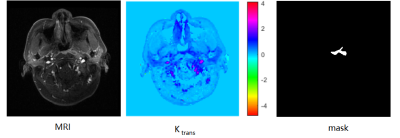
where v_p is the fractional plasma volume per unit of tissue volume and v_e is the extravascular space volume. Contrast agent concentration C_p(t) in plasma was obtained using a population-based arterial input function (AIF). The K_trans map obtained according to the above equation is shown in Figure 1.
We used the obtained K_trans maps together with the DCE-MRI of the sixth phase as input to the model. The ratio of the training set, validation set and test set is approximately 8:1:1. The Dice, Hausdorff distance (HD) and average symmetric surface distance (ASSD) were used as evaluation indicators.

RESULTS

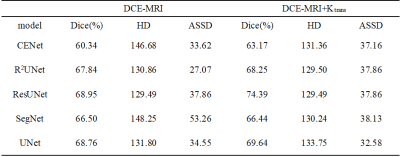
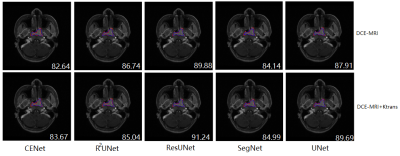
Table I shows the test results for single modality (DCE-MRI) and multimodality (DCE-MRI+K_trans) under different models. Comparing the results of Dice, the comparison of multimodal and single modalities on the 5 typical segmentation models were CENet (63.17 vs 60.34), R²UNet (68.25 vs 67.84), ResUNet (74.39 vs 68.95), SegNet (66.44 vs 66.50) and UNet (69.64 vs 68.76). Comparing the results of HD, the comparison of multimodal and single modalities on five typical segmentation models were CENet (131.36 vs 146.68), R2UNet (129.50 vs 130.86), ResUNet (129.49 vs 129.49), SegNet (130.24 vs 148.25) and UNet (133.75 vs 131.80). Comparing the results of ASSD, the comparison of multimodal and single modalities on the five typical segmentation models were CENet (37.16 vs 33.16), R2UNet (37.86 vs 27.07), ResUNet (37.86 vs 37.86), SegNet (38.13 vs 53.26) and UNet (32.58 vs 34.55). The segmentation results for each method are shown in Figure 2.

DISCUSSION

As seen in Table I, it is possible to improve segmentation using a multimodal approach, with the greatest increase in dice values in ResUNet, where dice improved by 5.44%. With the exception of SegNet, the dice of all the models have been improved. As dice responds to the overall segmentation effect, it indicates that the K_trans map can provide more information on the overall shape of the tumor. HD and ASSD respond to the effect of edge segmentation of the tumor. The HD and ASSD results show that multimodality is not overly helpful in improving the edge segmentation of the model, but it is helpful in keeping the edge segmentation results stable. The mean ± standard deviation of HD and ASSD for multimodal and single modality were HD (130.87±1.59 vs 137.45±8.25) and ASSD (36.72±2.09 vs 37.27±8.73).

CONCLUSION

Our experiments show that the pharmacokinetic feature K_trans is effective in aiding deep learning models to segment tumor regions; K_trans provides more information about the tumor shape, making the overall segmentation results more accurate and the edge segmentation more stable.

Acknowledgements

No acknowledgement found.