Synopsis

Keywords: Machine Learning/Artificial Intelligence, Image Reconstruction

Domain-transform manifold learning is a trained reconstruction approach where care needs to be taken to appropriately represent the forward encoding model during training, including for example the numerical properties of the source sensor data, phase relationship of complex sensor data, and field-of-view to prevent artifacts arising in the reconstruction. Here, we study the role that the training corpus and the numeral properties of the training have on the performance of the reconstruction of MRI data and demonstrate reconstruction artifacts that result from inference on out-of-training-distribution data if the training data is not augmented sufficiently.

Introduction

All supervised learning approaches from classification to image reconstruction require the curation of a training dataset that leads to the robustness and generalization of a deployable model. Automated Transform by Manifold Approximation (AUTOMAP) is a deep learning framework that employs domain-transform manifold learning to reconstruct MRI images from raw sensor k-space data¹. Koonjoo et. al showed that the domain specificity of the training data plays an important role. AUTOMAP trained on forward-modeled synthetic roots and synthetic vascular tree structures performed significantly better on real-world root raw MRI k-space data when compared to AUTOMAP trained on forward-encoded brain images². To form a deployable AUTOMAP model, we need to construct a training dataset that represents the forward encoding appropriately, incorporating numerical properties of the source sensor data, phase relationship of complex sensor data, and multiple field-of-views (FOV) among other properties to prevent artifacts arising in the reconstruction. We test and demonstrate that artifacts can occur and be diminished for two properties, 1) training AUTOMAP with and without a range of image-domain FOV and 2) training AUTOMAP with and without the numerical properties of engineered adversarial noise³. Especially when reconstructing medical images, it is paramount to study the properties of the training dataset so that a model generalizes and doesn’t lead to a misdiagnosis.

Materials and Methods

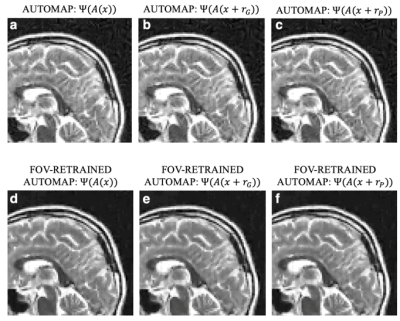
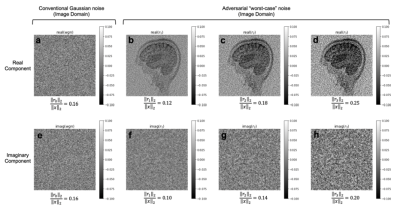
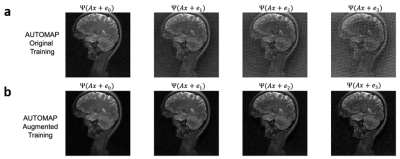
We trained AUTOMAP models to study two properties of training datasets, robustness to FOV artifacts and adversarial noise. The training images were 2D T1-weighted brain MR images acquired at 3 T collected from the MGH-USC Human Connectome Project (HCP) public dataset⁴. For the FOV experiments, we needed to curate two datasets, one with a single FOV (random samples shown in Fig 1a) and one with multiple FOVs (random samples shown in Fig 1b). Fig 1c was used to showcase artifacts from the different models in Fig 2 and discussed in the results. To study the robustness to adversarial noise and the role of numerical properties of a dataset, the adversarial noise was generated using a gradient ascent with momentum perturbation search algorithm³. The original AUTOMAP was trained to output positive, magnitude images. The adversarial noise pushed this boundary to generate negative and complex-valued noise in the image domain. When applied in the k-space domain, the numerical properties pushed AUTOMAP beyond its reconstruction capabilities leading to artifacts. In Fig 3, we show the adversarial noise is highly structured and contains negative values. Instead of training on positive, magnitude-only images, we added randomized constant offsets (between -0.1 and +0.1) to the training images and retrained AUTOMAP. We show the results of both these models in Fig 4.

Results and Discussion

The top row in Fig 2 demonstrates what artifacts arise when a model trained on a single FOV is tested on an out-of-distribution FOV in the image domain. All conditions, without noise (Fig 2a), Gaussian noise (Fig 2b), and Poisson noise (Fig 2c), display artifacts (particularly in the dark image background region). After retraining AUTOMAP with multiple FOVs, under both noiseless and noise-applied conditions, the artifacts were significantly reduced (bottom row Fig 2 d-f). We tested and demonstrated how important the role of training data augmentations is through something as simple as incorporating multiple FOVs in the training data. In a clinical setting, these same artifacts could lead to a misdiagnosis or a delay as the clinical practitioners may not be aware where the fault occurred. We also demonstrate the role of the numerical properties of a training dataset and how artifacts introduced by adversarial noise can be avoided. Fig 4a (top row) demonstrates artifacts that arise from adversarial noise. After training a network on images that contain negative offsets due to the adversarial noise consisting of negative values, the retrained AUTOMAP model doesn’t contain the same artifacts in Fig 4b (bottom row). If adversarial noise is a concern, we demonstrate it is important to study the numerical properties of the dataset and augment it appropriately so the model can generalize in practice.

Conclusion

To train a deployable image reconstruction model, the role of training data augmentations and numerical properties of datasets can’t be underestimated. We trained two models, with a single FOVs and a range of FOVs in the image domain. The model trained on a single FOV produces artifacts on an out-of-distribution FOV image while the properly trained model doesn’t. We also studied the role of numerical properties. When adversarial noise pushes a network beyond its training dataset numerical properties, we observe artifacts. If those numerical properties are incorporated into the training dataset, the artifacts are significantly reduced.

Acknowledgements

We acknowledge support for this work from the National Science Foundation Graduate Research Fellowship under Grant No. DGE-1840990 and the NSF NRT: National Science Foundation Research Traineeship Program (NRT): Understanding the Brain (UtB): Neurophotonics DGE-1633516NSF.