Synopsis

Keywords: Machine Learning/Artificial Intelligence, Image Reconstruction

Compressed Sensing is widely used for accelerating acquisitions of MR images. Deep learning methods have been introduced to CS-MRI reconstruction to improve image quality and computation speed. Here we introduce a new shrinkage function with adaptive threshold selection for Model-driven deep learning networks to suppress aliasing artifacts by utilizing the information on each feature map. We combine our adaptive threshold selection module with ISTA-Net, and demonstrate that the method can reduce reconstruction errors while preserving structural details effectively.

Introduction

Compressed Sensing (CS) theory enables the reconstruction of sub-Nyquist-sampled data by utilizing the sparsity priors of MR images. CS-MRI is widely used to accelerate image acquisitions^1,2. Recently, deep learning has been applied to CS-MRI reconstruction. Model-driven deep learning networks, such as ISTA-Net³ and Admm-Net⁴, have demonstrated success than conventional computation techniques, and provide superior reconstruction results for highly undersampled k-space data.
By adjusting the threshold that filters noise in the sparse transform domain, classic CS-MRI achieves a balance between artifact removal and detail preservation. An adaptively determined threshold from the transform domain may improve the reconstruction quality when compared to a fixed one5,6. Inspired by this, we design a new deep learning architecture that integrates ISTA-Net and an adaptive threshold selection module based on Bayes Shrinkage⁷, named aISTA-Net, for CS reconstruction. Our result suggests the efficacy of the proposed adaptive shrinkage module for improving the reconstruction performance.

Method

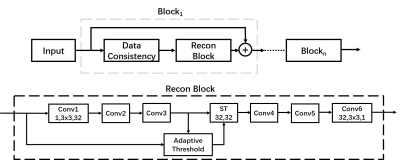
Theory
The CS reconstruction problem can be written as¹
$$x=arg\min_{x} \left \| Ax-b \right \| _{2}^{2}+\lambda \left \| \Psi x \right \|_{1} $$
where $$$A$$$ denotes encoding matrix, $$$y$$$ denotes acquired k-space data, $$$\Psi$$$ denotes sparse transform, and $$$x$$$ is the image to be reconstructed. Proximal gradient decent is used for reconstruction:
$$x_{k+1}=P\left \{ x_{k}-t_{k}\bigtriangledown \left ( Ax_{k}-b \right ) \right \} $$
where $$$P$$$ is the proximal operator
$$P\left ( x \right ) = \Psi ^{-1}S_{\lambda } \left ( \Psi x \right ) $$
and $$$S_{\lambda }$$$ stands for soft-thresholding function. The above function is also utilized for sparsity-based image denoising. An example of this is wavelet shrinkage, in which noise in the wavelet domain is filtered using a hard/soft threshold function. Since the aliasing artifacts caused by under-sampling are noise-like in the transform domain^1,2, one observes
$$\Psi m = \Psi y + n$$
where $$$m$$$ is the aliased image, $$$y$$$ is the truth value, $$$n$$$ is the noise-like incoherent artifacts. Assuming that coefficients of natural images in sparse transform domain obey a Laplacian distribution, the shrinkage threshold can be determined by minimizing the mean-squared error between the denoised coefficients $$$\Psi \hat{m}$$$ and true coefficients $$$\Psi y$$$ , according to Bayes Shrinkage theory⁷:
$$ \lambda_{A} = \frac{\sigma ^{2}}{\sigma_{x} } $$
where $$$\sigma$$$ stands for the noise level $$$n$$$, $$$\sigma_{x}$$$ stands for standard deviation of sparse domain.
In ISTA-Net, a learnable nonlinear transform function G consisting of several convolution blocks is adopted to replace the original sparse transform,
$$x=arg\min_{x} \left \| Ax-b \right \| _{2}^{2}+\lambda \left \| G x \right \|_{1} $$
Similar to traditional reconstruction methods, ISTA-Net utilizes the proximal gradient descent method. Thus the same shrinkage function P is utilized to filter the general transform domain. Based on the coefficients of feature maps, an adaptive threshold similar to the Bayes Shrinkage threshold can be obtained to distinguish signals from aliasing artifacts.
Therefore, we propose an aISTA-Net with $$$\lambda$$$ replaced by $$$\lambda_{A}$$$. Fig. 1 depicts the aISTA-Net architecture. The adaptive threshold selection module computes $$$\lambda_{A}$$$ from previous input and feature maps. The median estimation of the k-space of the input aliased image before each iteration is used to determine the noise level of incoherent artifacts. $$$\sigma_{x}$$$ is calculated from each feature map.
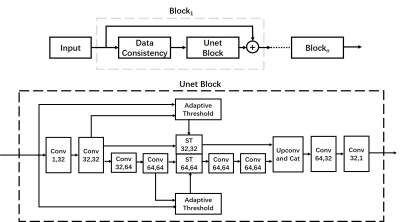
We further generate an auISTA-Net combining a Unet architecture and the adaptive threshold selection module. The abbreviated architecture of auISTA-Net is shown in Fig. 2. In practice we employ a Unet of 3-levels and 6 convolution layers on each level.

Data acquisition
The network is trained on public dataset IXI⁸. 6500 slices from 2D PD-weighted fully-sampled brain images of 50 subjects are chosen as training data. They are under-sampled using a variable density Poisson disk sampling mask with an acceleration factor of 6 (single channel data). After training, we test the network on 10 subjects with 1300 slices.
The proposed aISTA-Net and auISTA-Net are trained using a combination of Multiscale-Structural Similarity(MSSIM) and L1 as the loss function:
$$Loss=0.84MSSIM\left ( t,x \right ) +(1-0.84)\left \| t-x \right \| _{1}$$
where $$$t$$$ denotes target image, $$$x$$$ denotes reconstructed image. ISTA-Net and uISTA-Net, which share the same design as the proposed methods but lack the adaptive threshold selection module, are trained for comparison.

Result

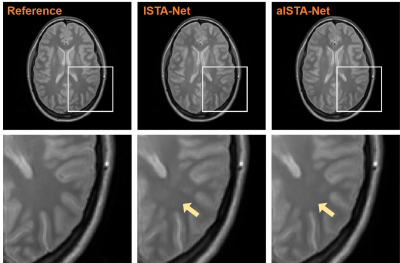
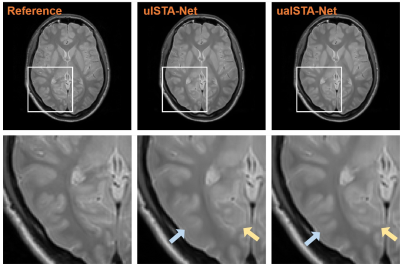
Fig. 3 shows the reconstruction results from ISTA-Net and aISTA-Net. aISTA-Net provides better result with less reconstruction errors and better preserved structural details.
The results from uISTA-Net and auISTA-Net are displayed in Fig. 4. auISTA-Net fixes several fake structures that are present in the result of uISTA-Net. Additionally, auISTA-Net offers sharper edges and more details pointed by the blue arrow.
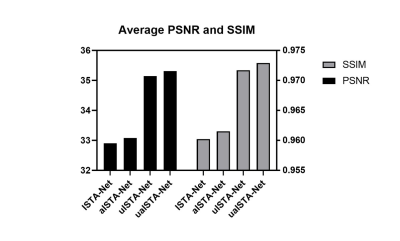
The average PSNR and SSIM in Fig. 5 also demonstrate the efficacy of the proposed adaptive threshold selection module.

Discussion and Conclusion

In this work, we develop an adaptive threshold selection module to enforce the performance of state-of-art model-based deep learning method for CS reconstruction. Experiments demonstrate that the proposed method can effectively reduce reconstruction errors while preserving detailed information of anatomical structures. We expect refinement of the proposed method with larger training dataset. Further study on verifying the proposed module with multi-coil data will be explored in the future.

Acknowledgements

No acknowledgement found.