3708
Perturbation loss with carrier image reconstruction: A loss function for optimized point spread functions
R. Marc Lebel1,2
1GE Healthcare, Calgary, AB, Canada, 2Radiology, University of Calgary, Calgary, AB, Canada
1GE Healthcare, Calgary, AB, Canada, 2Radiology, University of Calgary, Calgary, AB, Canada
Synopsis
Keywords: Machine Learning/Artificial Intelligence, Image Reconstruction
Deep learning (DL) assisted image reconstructions are becoming state-of-the art, producing better image quality and/or enabling higher acceleration rates than achievable with conventional methods. DL networks are used to mitigate noise amplification while retaining important signal characteristics. However, typical loss functions produce object-dependent noise alterations and non-uniform point-spread functions. Here we present a method for training networks that prioritizes maximizing the point spread function to ensure maximal detail retention.Introduction
Deep learning image reconstruction algorithms, particularly those leveraging physics models [1, 2], have become state-of-the-art for achieving high acceleration factors. These networks are often trained with a mean absolute error (MAE) or mean squared error (MSE) loss, which estimates the expectation value of noisy data – essentially providing a low-noise reconstruction. The disadvantage of this approach is that it can over-regularize images, resulting in some loss of detail. Furthermore, the regularization is spatially varying and anatomy dependent with excessive smoothing in uniform tissues.Here we propose an alternative (or additional) loss function that promotes detectability in the reconstructed images. The proposed loss function teaches the network to remove coherent and incoherent aliasing and regularizes noise to maximize retention of small features. It serves as an alternative to MAE/MSE when sharper images are desired but some additional noise is tolerable. The proposed loss function is unsupervised and does not require fully sampled label data but still trains with MR data.
Methods
This work was inspired by methods for measuring the point-spread function (PSF) of DL-based reconstructions and by the pseudo-replicate method for measuring g-factor [3, 4].The proposed method is summarized in Figure 1. It starts by creating a small perturbation in image space. The content of this image is of secondary importance but nominally consists of sparse random points. The amplitude of these points must be sufficiently small that when added to the data they do not alter the image appearance substantially. The amplitude must be sufficiently large to avoid numerical underflow. The perturbation is converted to multi-channel k-space and undersampled in the same way as the imaging data. Two image reconstructions are performed: one with the original unperturbed data; the second with the added perturbation. The reconstructed images are subtracted leaving only the reconstructed perturbation, which is compared to the original with a reduction metric such as MAE.
Reconstruction performance was quantified by computing the relative noise of reconstructed images (using the pseudo-replica method) and by computing the relative sharpness, defined as the fraction of a small perturbation added to an input voxel that is retained in that location after reconstruction (closely related to the PSF). The ratio of sharpness-to-noise gives a summary of overall performance. We compared unregularized iterative SENSE (128 iterations), an unrolled network using a self-supervised MAE loss, and an unrolled network using the proposed loss.
Results
Figure 2 shows the reconstruction performance on an MPRAGE scan acquired with prospective 6-fold variable density Poisson disc acceleration. Iterative sense provides the sharpest image but suffers from extreme noise amplification, yielding a low sharpness-to-noise map. Self-supervised training yields a very low-noise image but with relatively poor sharpness. Furthermore, the sharpness and noise are anatomy dependent, making low-contrast detectability regionally variable. Interestingly, the overall performance of this training remains very high. The proposed loss function balances sharpness and noise amplification to maximize feature detectability. The sharpness is generally higher than with self-supervised loss but so is the reconstructed noise. The relative sharpness-to-noise is reasonably high and interestingly is not anatomy dependent.Figure 3 presents reconstructed images with 4-, 6-, 8-, and 10-fold prospective acceleration. Iterative SENSE appears sharp but is very noisy. Self-supervised training yields images that are very clean and overall of very high quality. The proposed loss maintains a natural appearance with a balance of noise and subtle feature retention. Both self-supervised and the proposed loss are effective but optimize for different image characteristics.
Discussion
The proposed loss function uses a small perturbation overlaid on undersampled data. The perturbation must be small since we want the network to learn to reconstruct the image rather than to specifically reconstruct the perturbation at the expense of the image. In this sense, the image is used as a carrier signal for the perturbation. The reconstruction must balance noise amplification with reconstruction fidelity so that the perturbation is preserved after image subtraction.The self-supervised loss function works very well, as shown by the relative sharpness-to-noise ratio in Figure 2 but achieves this success via aggressive noise suppression. The proposed loss optimizes small feature retention, which produces objectively sharper images but with more noise.
Conclusion
The proposed loss function optimizes feature detectability and provides an alternative or complimentary loss function to MAE or MSE based losses. This method is unsupervised; training is possible with prospectively or retrospectively accelerated data.Acknowledgements
The author acknowledges Suryanarayanan (Shiv) Kaushik for valuable discussions.References
[1] Hammernik K, et al. Learning a variational network for reconstruction of accelerated MRI data. Magn Reson Med. 2018 Jun;79(6):3055-3071. doi: 10.1002/mrm.26977.[2] Malkiel I, et al. Densely Connected Iterative Network for Sparse MRI Reconstruction. ISMRM 2018. 3363.
[3] Lauer K, et al. Assessment of resolution and noise in MR images reconstructed by data driven approaches. ISMRM 2022. 0303.
[4] Robson PM, et al. Comprehensive quantification of signal-to-noise ratio and g-factor for image-based and k-space-based parallel imaging reconstructions. Magn Reson Med. 2008 Oct;60(4):895-907. doi: 10.1002/mrm.21728.
Figures
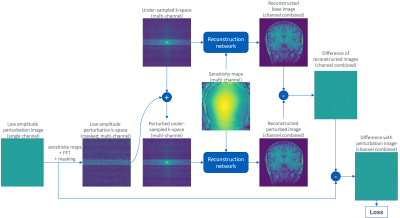
Figure 1: Overview of proposed unsupervised loss for training DL reconstructions. The reconstruction network to be trained accepts k-space and sensitivity maps and returns reconstructed k-space or images. The reconstruction is done twice: once with the normal data; a second time with mildly perturbed data. The perturbation comes from a separate low-amplitude image, converted to under-sampled multi-channel k-space. The difference of the reconstructed images should match the known perturbation and an L1 or L2 norm yields a loss metric.
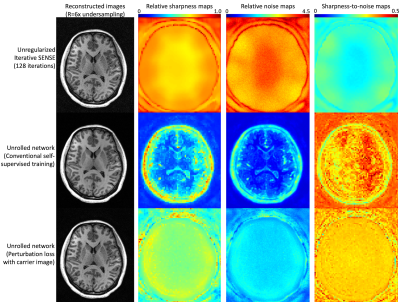
Figure 2: Comparison of reconstructions with 6x
accelerated MPRAGE: (top) unregularized SENSE, (middle) unrolled DL
network with conventional training, (bottom) unrolled DL network with
the proposed perturbation loss. SENSE produces the sharpest image but
with extreme noise amplification. A conventionally trained DL network
produces a clean image but with compromised and anatomically dependent
sharpness. A DL network with the proposed loss provides high relative
sharpness yet limited noise amplification.
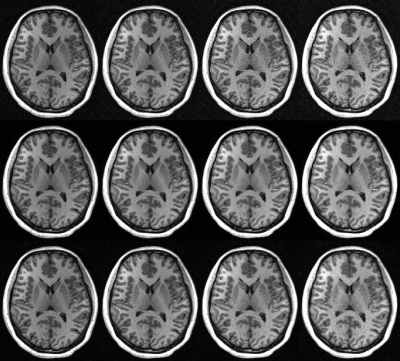
Figure 3: Images reconstructed with iterative SENSE (top
row), DL network with conventional training (middle row), and an unrolled DL
network with the proposed perturbation loss (bottom row). Images were acquired
with acceleration rates of 4x (left), 6x (middle left), 8x (middle right), and
10x (right). Perturbation loss provides an alternative to self-supervised loss
and offers a balance of increased sharpness at the expense of some increased
noise.
DOI: https://doi.org/10.58530/2023/3708