3704
Deep learning-based acquisition protocol optimization and parameter estimation for diffusion exchange spectroscopy1College of Information Science and Electronic Engineering, Zhejiang University, Hangzhou, China, 2Key Laboratory of Biomedical Engineering of Ministry of Education, College of Biomedical Engineering and Instrument Science, Zhejiang University, Hangzhou, China, 3School of Medicine, Zhejiang University, Hangzhou, China
Synopsis
Keywords: Machine Learning/Artificial Intelligence, Data Acquisition
We propose a deep-learning-based method to optimize acquisition protocol and estimate parameter for diffusion exchange spectroscopy. A unified framework has been carefully designed to achieve both goals simultaneously. Using this framework, the acquisition protocol can be directly optimized with an objective function that minimizes the parameter estimation errors, regardless of its degree of freedom. The experimental results from Monte Carlo simulations show that the proposed method outperforms the existing methods in both accuracy and precision of parameters’ estimation. Besides, it speeds up the calculation by 480 times.Introduction
Water transport across biological membrane is one of important functions for living cells1, which has been proved to be potential biomarkers for pathological conditions such as cancer and brain edema2. Therefore, a non-invasive method to detect the transmembrane water exchange processes in-vivo is urgently needed. Diffusion exchange spectroscopy (DEXSY)3,4, comprising two pulse gradient spin echo (PGSE) blocks separated by a variable mixing time $$$t_m$$$, is proposed to measure the rate of water exchange across membrane, which, however, suffers from long acquisition time.To accelerate DEXSY for in-vivo applications, a series of acquisition protocol and analysis methods have been proposed5-10. However, existing methods are still not satisfactory for two reasons. From the perspective of acquisition protocol settings, these methods5-8 impose extra constraints to avoid large number of degrees of freedom. Filter exchange Spectroscopy (FEXSY)5 replaced the first variable gradient PGSE block of the DEXSY with a fixed gradient filter block. Anti-diagonal strategy6 constrained the sum of first gradient PGSE and second gradient PGSE to be constant. Diagonal strategy7 commanded the equality between the two gradient PGSE block. From the other perspective of objective function, the acquisition protocol is optimized for minimal measurement variance in the relevant physiological parameters based on Cramer-Rao lower bound (CRLB)9-10, rather than minimal physiological parameter error.
To address these issues, we propose a Learning-based Acquisition Protocol Optimization and Parameter Estimation (L-APOPE) method which is an end-to-end framework to achieve acquisition protocol optimization and fast parameter estimation simultaneously. Compared to existing methods9-10, acquisition protocol optimization in L-APOPE is fully guided by the minimum parameter estimation error, which is a direct optimization method. Besides, we don’t introduce any constraints to acquisition protocol and retain its own degrees of freedom. The method is demonstrated in a simulated cell suspension system.
Theory
The simulated cell suspension system consists of the intra- and extracellular compartments (Fig.1A). The physiological parameters affecting the signal attenuation are listed in Fig.1C. Here, we introduce operators to calculate the signal evolution according to DEXSY pulse sequence (Fig.1B):$$S_{DEXSY}=\mathbf{I}\times\mathbf{OP_1}\times\mathbf{OP_m}\times\mathbf{OP_2}\times \mathbf{S_0}$$
Where $$$\mathbf{I}=(1,1)$$$ and $$$\mathbf{S_0}=(f_i^{eq}*S_0,f_e^{eq}*S_0)^T$$$. In the first PGSE block, $$$\mathbf{OP_1}=e^{-b_1\mathbf{D}}$$$, where $$$b_1$$$ denotes diffusion weighting and $$$\mathbf{D} =\left ( \begin{matrix}D_i&0\\0&D_e\end{matrix} \right ) $$$. Then after mixing time $$$t_m$$$, $$$\mathbf{OP_m}=e^{-t_m*(\mathbf{R1+K})}$$$, where $$$\mathbf{R1}=\left(\begin{matrix} 1/T1_i & 0\\0 & 1/T1_e\end{matrix} \right )$$$ and $$$\mathbf{K} = \left ( \begin{matrix} k_{ie} & -k_{ei}\\ -k_{ie} & k_{ei}\end{matrix} \right )$$$. Finally, the operator in the second PGSE block is $$$\mathbf{OP_2} = e^{-b_2\mathbf{D}}$$$, where $$$b_2$$$ denotes diffusion weighting.
Methods
The proposed L-APOPE consists of two modules (Fig.2). The acquisition protocol optimization module takes the ground-truth of parameters as inputs and simulates the signal evolution of DEXSY pulse sequence. It generates signals based on Eq.(1), 10 different $$$t_m$$$ are fixed as uniform sampling from 10 to 350 $$$ms$$$ refer to strategy3 and $$$(b_1,b_2)$$$ are 15 sets of trainable parameters. Then we generate signals with Rician distributed noise $$$\widetilde{S_{DEXSY}}$$$ to simulate the real signal with noise as follows:$$\widetilde{S_{DEXSY}} = \sqrt{(S_{DEXSY}+noise1)^2+(noise2)^2}$$
Where $$$noise1$$$ and $$$noise2$$$ are two independent Gaussian noise components and the standard deviation (SD) of them is defined based on SNR.
The parameter estimation module consists of 6 fully-connect layers followed by ELU activation layer except for the last layer, which takes $$$\widetilde{S_{DEXSY}}$$$ as input and outputs four estimated parameters $$$\hat{D_i}$$$, $$$\hat{D_e}$$$, $$$\hat{f_i^{eq}}$$$ and $$$\hat{k_{ie}}$$$.
The entire network is trained with Adam optimizer. The loss function is the sum of the mean squared errors (MSE) between the ground truth and the estimated values as follows:
$$L=MSE(D_i,\hat{D_i})+MSE(D_e,\hat{D_e})+MSE(f_i,\hat{f_i})+MSE(k_{ie},\hat{k_{ie}})$$
Where each parameter has been normalized with relevant min-max value to keep their respective equal weights in the loss function.
Results
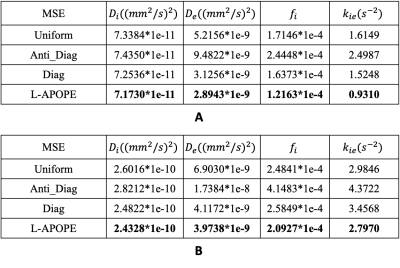
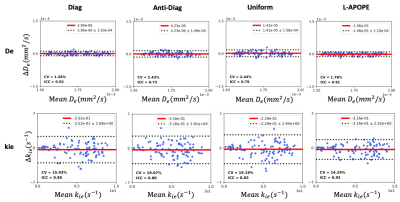
All of the experiments were conducted on a simulation dataset (Fig.1C) at SNR=40 ($$$b_1=b_2=0 {mm}^{2}/s,t_m=10ms$$$). Fig.3 showed the MSE results of the different acquisition protocols with two parameter estimation methods: the Deep Neural Network (DNN) method (Fig.3A) and the Non-Linear Least Squares (NLLS) method (Fig.3B). It is obviously that the acquisition protocol optimized by L-APOPE combined with DNN-based parameter estimation method achieves the lowest MSE. Especially for $$$k_{ie}$$$, it reduces the MSE by 38.9% compared to the suboptimal Diagonal-strategy.Bland-Altman plots (Fig.4) of test-retest repeatability experiments were shown to compare the precision performance of different acquisition protocols. Here, the parameter estimation method was fixed as DNN. For $$$k_{ie}$$$, L-APOPE achieved the lowest SD and coefficient of variation (CV)11 and highest intraclass correlation (ICC)12. For $$$D_e$$$, the performance of L-APOPE was similar to that of Diagonal-strategy.
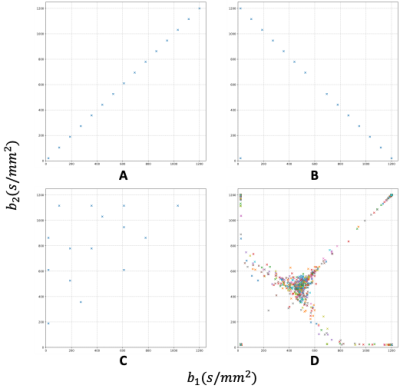
Fig.5 shows the subsampling schemes of different acquisition protocols. Fig.5A, B and C show the subsampling strategy of Diagonal, Anti-diagonal and Uniform. Fig.5D presents the optimization results of 100 repeats with the same settings of L-APOPE, which shows a clear regularity, distributed along the diagonal and anti-diagonal lines.
Our proposed method could also speed up the parameter estimation processes. For 100,000 sets of experiments, the computation time of DNN and NLLS are 10s and 1h19m56s, respectively.
Discussion and conclusion
Optimal acquisition protocols and parameter estimation methods are needed to facilitate the in-vivo application of DEXSY. Here, we proposed a deep-learning-based method, L-APOPE, to achieve DEXSY acquisition protocol optimization and accurate parameter estimation in a uniform framework, which largely improve the accuracy and precision of DEXSY parameters’ measurement. Further testing on in-vivo data will be performed in future.Acknowledgements
No acknowledgement found.References
1. Benga G. WATER TRANSPORT IN RED BLOOD CELL MEMBRANES. :53.
2. Bai R, Li Z, Sun C, Hsu YC, Liang H, Basser P. Feasibility of filter-exchange imaging (FEXI) in measuring different exchange processes in human brain. NeuroImage. 2020;219:117039. doi:10.1016/j.neuroimage.2020.117039
3. Callaghan P T, Furo I. Diffusion-diffusion correlation and exchange as a signature for local order and dynamics[J]. The Journal of chemical physics, 2004, 120(8): 4032-4038.
4. Eriksson S, Elbing K, Söderman O, Lindkvist-Petersson K, Topgaard D, Lasič S. NMR quantification of diffusional exchange in cell suspensions with relaxation rate differences between intra and extracellular compartments. Motta A, ed. PLoS ONE. 2017;12(5):e0177273. doi:10.1371/journal.pone.0177273
5. Åslund I, Nowacka A, Nilsson M, Topgaard D. Filter-exchange PGSE NMR determination of cell membrane permeability. Journal of Magnetic Resonance. 2009;200(2):291-295. doi:10.1016/j.jmr.2009.07.015
6. Cai TX, Benjamini D, Komlosh ME, Basser PJ, Williamson NH. Rapid detection of the presence of diffusion exchange. Journal of Magnetic Resonance. 2018;297:17-22. doi:10.1016/j.jmr.2018.10.004
7. Ramadan S. Diffusion-Exchange Weighted Imaging. Magn Reson Insights. 2009;3:MRI.S3504. doi:10.4137/MRI.S3504
8. Ordinola A, Cai S, Bai R, Özarslan E. Characterizing structure and diffusion exchange: Comparing subsampling strategies. :1.
9. Alexander DC. A general framework for experiment design in diffusion MRI and its application in measuring direct tissue-microstructure features. Magn Reson Med. 2008;60(2):439-448. doi:10.1002/mrm.21646
10. Powell E, Battiston M, Parker GJ. ISMRM 2021-Diffusion-filtered exchange measurements of blood-brain barrier permeability to wate. :4.
11. Huang H. Reliable estimation of brain intravoxel incoherent motion parameters using denoised diffusion‐weighted MRI. NMR in Biomedicine. 2020;33(4). doi:10.1002/nbm.4249
12. Koo TK, Li MY. A Guideline of Selecting and Reporting Intraclass Correlation Coefficients for Reliability Research. Journal of Chiropractic Medicine. 2016;15(2):155-163. doi:10.1016/j.jcm.2016.02.012
Figures
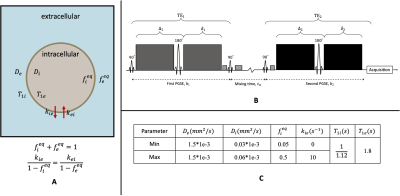
Figure 1. Schematic of cell suspension system and DEXSY pulse sequence. (A). Cell suspension system is modelled with intra- and extracellular model, where and denote diffusivities and volume fractions respectively, denotes the exchange rate from intracellular to extracellular. (B). Illustration of the DEXSY pulse sequence. (C). Simulation data setup.