3703
Theoretical guaranteed unfolding method for k-space interpolation in a self-supervised manner
Chen Luo1,2, Zhuoxu Cui2, Huayu Wang1,2, Qiyu Jin1, Guoqing Chen1, and Dong Liang2
1Inner Mongolia University, Hohhot, China, 2Shenzhen Institute of Advanced Technology,Chinese Academy of Sciences, Shenzhen, China
1Inner Mongolia University, Hohhot, China, 2Shenzhen Institute of Advanced Technology,Chinese Academy of Sciences, Shenzhen, China
Synopsis
Keywords: Machine Learning/Artificial Intelligence, Image Reconstruction
Recently, iterative algorithm driven deep neural network unfolding methods have been successfully applied to MRI. However, the network replaces the original algorithm structure and mathematical properties such as interpretability and convergence of the original algorithm are not guaranteed. Fortunately, the k-space-filled Hankel low rank can naturally be associated with convolutional networks. Given this, we propose an unfolding method for k-space-filling, which guarantees convergence to the unique real MR image. Furthermore, we train this network in a self-supervised manner to cope with scenarios where fully sampled data are difficult to obtain. Finally, numerical experiments validate the effectiveness of the proposed method.Introduction
MRI, as a non-intrusive medical imaging technique, generates high-resolution images. Since MRI has no radiation and will not injure patients’ health, it has been widely used in clinical diagnosis. Despite the merits mentioned above, the technique has the shortcoming of long scanning time.Parallel imaging (PI) [1] and compressed sensing (CS) [2][3] reduce MRI scan time from hardware and algorithm, respectively. Most methods in PI or CS solve the MR image reconstruction with fidelity term and regularization term to recover MR image. To improve the reconstruction accuracy and speed of the traditional regularization algorithm, methods [4][5][6][7] unfold the iterative algorithm architecture via deep learning to eliminate the artifacts in image domain. Nevertheless, the learned regularization term or proximity operator of numerous unfolding networks loses its mathematical properties. In other words, what the network learns is not guaranteed to be the component required in method. Hence it is difficult to guarantee the reconstruction theory.
It is worth noting that k-space-filled Hankel low rank [8,9] can naturally be associated with convolutional networks. Inspired by this fact, we propose an unfolded projected gradient descent (PGD) algorithm with theoretical guarantees of convergence. In this work, the main contributions are (a) training the network to learn gradient descent steps of PGD algorithm without changing its convergence property, which overcome the obstacle of general unfolding methods and implement non-linear SLR with theoretical guarantees. (b) ensuring that the solution of our unfolded PGD algorithm is a unique convergence point after training by deep equilibrium (DEQ) model [10]. (c) carrying out a self-supervised strategy to enhance the adaptability of the model, and achieving convincing results shown that our method performs effectively.
Method
SLR is a crucial method of MRI reconstruction, which transforms parallel MRI reconstruction of undersampled k-space data $$$b$$$ into a minimization problem as$$\left\{\begin{matrix} \min_{\hat{x}}\left \| H(\hat{x})S \right \|_{F}^{2} \\ \mathrm{s.t.} \quad M\hat{x} = b\end{matrix}\right. \qquad (1)$$where $$$\hat{x}$$$ denotes the multicoil k-space data to be recovered, $$$H(\cdot)$$$ is Hankel operator, $$$S$$$ is Fourier domain representation of coil sensitivity and $$$M$$$ denotes the sampling pattern. Owing to the commutativity of convolution, $$$\left \| H(\hat{x})S \right \|_{F} = \left \| H(S)\hat{x} \right \|_{F}$$$ holds. In this study, we solve the problem by unfolding PGD method as follows, $$r_{k+1} = \hat{x}_{k}-\eta H(S)^{T}H(S)\hat{x}_{k} \qquad (2)$$$$\hat{x}_{k+1} = \mathcal{P}_{\{M\hat{x} = b\}}(r_{k+1}) \qquad (3)$$$$$\mathcal{P}_{\mathcal{C}}$$$ means the orthogonal projection on $$$\mathcal{C}$$$, i.e., $$$\mathcal{P}_{\mathcal{C}}(x) = \arg \min _{y \in \mathcal{C} }\left \| x-y \right \|$$$. Note that $$$ H(S)\hat{x} $$$ is equivalent to $$$\mathit{Cov}_{S}\hat{x}$$$ which denotes the Convolutional Neural Network (CNN) containing coil sensitivity information. The solution alternates between the following subproblems, $$r_{k+1} = \hat{x}_{k}-\eta \mathit{Cov}_{S}^{T}\mathit{Cov}_{S}\hat{x}_{k} \qquad (4)$$$$\hat{x}_{k+1} = \mathcal{P}_{\{M\hat{x} = b\}}(r_{k+1}) \qquad (5)$$of which the network $$$r_{k+1} = \mathcal{G}(\hat{x}_{k})$$$ represents the gradient descent of PGD. Our unfolded PGD avoids learning the regularization term and thus provides a theoretical guarantee for alternating iterative optimization. Inspired by [10][11], we can guarantee the above iterations to converge to the following solution set by DEQ.$$\Omega =\{ \hat{x}|M\hat{x}=b, \mathit{Cov}_{S}^{T}\mathit{Cov}_{S}\hat{x}_{k} = 0 \} =\{ \hat{x}|M\hat{x}=b, H(S)^{T}H(S)\hat{x}_{k}=0 \} \qquad (6)$$According to the matrix completion theory [12], we can guarantee that set $$$\Omega$$$ contains unique true solutions under certain conditions. In this paper, we consider the self-supervised scene as shown in Fig.1. Masking the measurement $$$b$$$ with a new sampling pattern $$$M'$$$ to get $$$b'=M'b$$$, the loss function is$$\mathcal{L} (b',b) = \left \| \mathcal{P}_{\{M\hat{x} = b\}}( \mathcal{G}(b') -b \right \|_{F}^{2} \qquad (7)$$The schematic diagram of our unfolded network architecture is shown in Fig. 2.Results
In this study, we utilize the training dataset (360 images of size $$$ 12 \times 256 \times 232 $$$) and testing dataset of [7]. All the data with 12 coils are transformed to the Fourier domain for training. Fig.3 illustrates the reconstruction of 6x accelerated brain data. We use peak signal-to-noise ratio (PSNR) for quantitative evaluation. The model is implemented on an Ubuntu 18.04 and Tesla V100 (GPU, 32 GB memory).Conclusions and Discussion
In this paper, we propose a deep learning SLR reconstruction algorithm with theoretical guarantees for the undersampled multi-coil k-space data. Instead of learning the regularization term or the threshold operator, we replace the Hank matrix with the network equivalently. Surprisingly, this substitution keeps the convergence of the PG method. We utilize DEQ to find the fixed point of our model to make sure our solution is optimal. Experimentally, we demonstrate that the proposed network can recover k-space data commendably. We believe that further research of our method may enable larger gains.Acknowledgements
This work was partially supported by the National Key R&D Program of China under Grant No. 2020YFA0712200; the National Natural Science Foundation of China under Grant Nos. 61771463, 81830056, U1805261, 61671441, 81971611, 12026603, 62106252, 12061052 and 62206273. Young Talents of Science and Technology in Universities of Inner Mongolia Autonomous Region (No. NJYT22090)References
- Pruessmann, K P et al. “SENSE: sensitivity encoding for fast MRI.” Magnetic resonance in medicine vol. 42,5 (1999): 952-62.
- Lustig, Michael, et al. "Compressed sensing MRI." IEEE signal processing magazine 25.2 (2008): 72-82.
- Lustig, Michael, David Donoho, and John M. Pauly. "Sparse MRI: The application of compressed sensing for rapid MR imaging." Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 58.6 (2007): 1182-1195.
- Zhang, Jian, and Bernard Ghanem. "ISTA-Net: Interpretable optimization-inspired deep network for image compressive sensing." Proceedings of the IEEE conference on computer vision and pattern recognition. 2018.
- Sun, Jian, Huibin Li, and Zongben Xu. "Deep ADMM-Net for compressive sensing MRI." Advances in neural information processing systems 29 (2016).
- Yaman, Burhaneddin, et al. "Self‐supervised learning of physics‐guided reconstruction neural networks without fully sampled reference data." Magnetic resonance in medicine 84.6 (2020): 3172-3191.
- Aggarwal, Hemant K., Merry P. Mani, and Mathews Jacob. "MoDL: Model-based deep learning architecture for inverse problems." IEEE transactions on medical imaging 38.2 (2018): 394-405.
- Pramanik, Aniket, Hemant Kumar Aggarwal, and Mathews Jacob. "Deep generalization of structured low-rank algorithms (Deep-SLR)." IEEE transactions on medical imaging 39.12 (2020): 4186-4197.
- Jacob, Mathews, Merry P. Mani, and Jong Chul Ye. "Structured low-rank algorithms: Theory, magnetic resonance applications, and links to machine learning." IEEE signal processing magazine 37.1 (2020): 54-68.
- Bai, Shaojie, J. Zico Kolter, and Vladlen Koltun. "Deep equilibrium models." Advances in Neural Information Processing Systems 32 (2019).
- Cui, Zhuo-Xu, et al. "Equilibrated Zeroth-Order Unrolled Deep Networks for Accelerated MRI." arXiv preprint arXiv:2112.09891 (2021).
- Recht, Benjamin. "A simpler approach to matrix completion." Journal of Machine Learning Research 12.12 (2011).
Figures
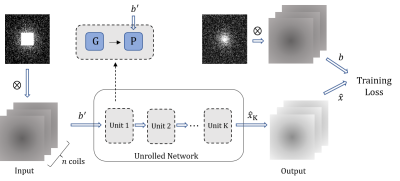
Fig.1 The self-supervised learning scheme
without fully sampled data. $$$G$$$ is the gradient descent. $$$P$$$ is the orthogonal
projection. $$$\otimes$$$ denotes dot product.
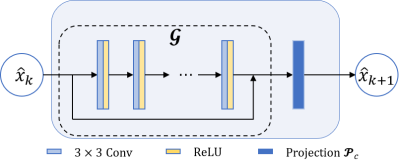
Fig. 2 Schematic diagram of the network
architecture of one unit: block $$$\mathcal{G}$$$ consists of
five-layer residual CNN in k-space, and $$$\mathcal{p}_{\mathcal{p}}$$$ is the projection
operator.
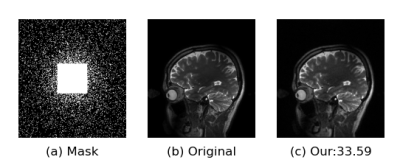
Fig. 3 Reconstruction result of the K-space network at $$$R = 6$$$. (a) Random
undersampling; (b) Ground truth; (c) Our result for self-supervised learning.
The number illustrates PSNR values in dB.
DOI: https://doi.org/10.58530/2023/3703