3649
Prediction of Eddy Current-Induced Background Phase Offsets in 2D Phase Contrast-MRI
Julio A. Oscanoa1,2, Matthew J. Middione2, Michael Loecher2, Ana Beatriz Solana3, Shreyas S. Vasanawala2, and Daniel B. Ennis2
1Department of Bioengineering, Stanford University, Stanford, CA, United States, 2Department of Radiology, Stanford University, Stanford, CA, United States, 3GE Healthcare, Munich, Germany
1Department of Bioengineering, Stanford University, Stanford, CA, United States, 2Department of Radiology, Stanford University, Stanford, CA, United States, 3GE Healthcare, Munich, Germany
Synopsis
Keywords: Flow, System Imperfections: Measurement & Correction, Phase-Contrast, Eddy currents
We propose a physics-driven approach for prediction of eddy current-induced background phase offsets in 2D PC-MRI. The method leverages the applied gradient waveforms and a circuit model to estimate the system-dependent parameters that govern the background phase. The aim is to use these parameters and the model to predict the background phase of clinical acquisitions from pulse sequence information only. Our method achieved an RMSE of 1.05 cm/s and adequate visual quality.Introduction
2D Phase Contrast MRI (PC-MRI) is routinely used in the clinic to quantify blood velocity and flow throughout the cardiovascular system. For accurate measurements, unwanted phase offsets must either be negligible or corrected1,2. Eddy current-induced velocity errors as little as 0.6cm/s can lead to 5% error in typical flow measurements or 10% error in typical cardiac shunt measurements3,4. Stationary tissue interpolation1,5,6 and stationary phantom7 correction techniques are effective at mitigating background phase errors. However, stationary tissue interpolation can be infeasible when insufficient stationary tissue is present in the image, while an additional stationary phantom measurement impedes clinical workflow.We present a physics-driven approach (Figure 1) that combines both of the above-mentioned methods. While stationary tissue interpolation estimates spatial polynomial coefficients specific to each scan, we aim to estimate the parameters that characterize the eddy-current impulse response of the system. The objective was to train a non-linear eddy-current model, with a set of phantom measurements, to predict the phase offset from the gradient waveforms, which would provide extra phase information and could potentially improve correction when the stationary tissue approach is deficient.
Theory
Eddy current-induced background phase offsets, $$$\Phi(\mathbf{r})$$$ can be modeled8 as: $$\Phi(\mathbf{r})=\gamma\int_0^{t_{TE}}B_{\epsilon}(\mathbf{r},t)dt\;\;[1]$$ (1) where $$$B_{\epsilon}$$$ is the eddy current-induced magnetic field, $$$\gamma$$$ is the gyromagnetic ratio, $$$t_{TE}$$$ is the echo time, and $$$\mathbf{r}=[r_x, r_y, r_z]\in\mathbb{R}^3$$$ is the spatial position. $$$B_\epsilon$$$ can be characterized8 as: $$B_\epsilon(\mathbf{r},t)=\sum^{K-1}_{k=0}\mathbf{c}_k(\mathbf{r})\left[\left\{ \epsilon_{x,k}\ast S_x\right\}(t)+\left\{\epsilon_{y,k}\ast S_y\right\}(t)+\left\{\epsilon_{z,k}\ast S_z\right\}(t)\right] \;\;[2]$$where $$$\mathbf{c}(\mathbf{r})=[1,r_x,r_y,r_z,r_x^2,r_y^2,\dots]\in\mathbb{R}^K$$$ is a vector of spatial terms that describe a spatial polynomial function, $$$\ast$$$ is the convolution operation, and $$$S_x,S_y,S_z$$$ and $$$\epsilon_{x,k},\epsilon_{y,k},\epsilon_{z,k}$$$ are the slew rates (from the gradient waveforms) and eddy-current impulse response functions, respectively, along the $$$x,y,z$$$ axes. Each of these functions can be characterized as a family of decaying exponentials with additional oscillatory terms9:$$\epsilon_{x,k}(t) = \sum^{N-1}_{n=0}\boldsymbol{\alpha}_ne^{-t/\boldsymbol{\tau}_n}+\sum^{M-1}_{m=0}\boldsymbol{\beta}_me^{-t/\boldsymbol{\kappa}_m}\sin(\boldsymbol{\omega}_mt+\boldsymbol{\phi}_m)\;\;[3]$$ where $$$\alpha,\tau,\beta,\kappa,\omega,\phi$$$ are system-dependent parameters that characterize the eddy-current impulse response. Combining Equations 1 and 2, $$$\Phi (\mathbf{r})$$$ can be rewritten10 as: $$\Phi(\mathbf{r})=\sum_{k=0}^{K-1}\mathbf{c}_k(\mathbf{r})\mathbf{p}_{k}\;\;[4]$$ where $$$\mathbf{p}\in\mathbb{R}^K$$$ and $$\mathbf{p}_k=\gamma\int^{t_{TE}}_0\left[\left\{\epsilon_{x,k}\ast S_x\right\}(t)+\left\{\epsilon_{y,k}\ast S_y\right\}(t)+\left\{\epsilon_{z,k}\ast S_z\right\}(t)\right]dt\;\;[5]$$These $$$\mathbf{p}$$$ coefficients, which characterize the phase offset as a spatial polynomial function, are the same parameters estimated in the stationary tissue interpolation method. Herein, we estimate the system-dependent parameters $$$\alpha,\tau,\beta,\kappa,\omega,\phi$$$ using the applied gradient waveforms and a non-linear regression procedure.Methods
2D PC-MRI datasets were acquired in a stationary gel phantom using a 3T SIGNA Premier system (GE HealthCare, Waukesha, WI) using a 30-channel phased array coil. Imaging was performed using a vendor provided gradient echo based, ECG-gated 2D PC-MRI sequence with the imaging parameters outlined in Table 1. 186 datasets were acquired (six VENCs, three scan planes, and 9-11 slices per scan). Additionally, the applied gradient waveforms for the x, y, and z axes of both velocity encodings were saved for each scan. All datasets were reconstructed using the vendor provided reconstruction pipeline.For each dataset, we obtained the measured background phase offset, $$$\hat{\Phi}_d$$$, via phase difference and the reference polynomial coefficients $$$\hat{p}_d$$$ via 2nd order polynomial fitting on $$$\hat{\Phi}_d$$$. Then, the 186 datasets were randomly divided into training (n=168, 90%) and testing datasets (n=18, 10%), where one slice was randomly selected per VENC and scan plane. The parameter fitting was performed by minimizing, over the training dataset, the following loss function:$$\mathcal{L}(\alpha,\tau,\beta,\kappa,\phi,\omega)=\sum^{D-1}_{d=0}\lambda_1\lVert \hat{\Phi}_d-\Phi(\text{S}_d,\alpha,\tau,\beta,\kappa,\phi,\omega)\rVert_2^2+\lambda_2\lVert\hat{p}_d-p(\text{S}_d,\alpha,\tau,\beta,\kappa,\phi,\omega)\rVert_2^2\;\;[6]$$ where $$$\text{S}_d=\{S_{x,d},S_{y,d},S_{z,d}\}$$$ are the slew rates for dataset $$$d$$$, and $$$\lambda_1$$$ and $$$\lambda_2$$$ are tunable hyperparameters. We tested different combinations of hyperparameters $$$\lambda_1$$$ and $$$\lambda_2$$$, and two main models: 1) exponential-only and 2) exponential plus oscillatory terms. We evaluated the performance quantitatively through RMSE and qualitatively through visual inspection.
Results
Figure 2 shows the RMSE and error distributions (after outlier removal) for all evaluated cases. In all cases, the RMSE for both training and validation datasets are very similar. Likewise, the model with both exponential and oscillatory terms performs better than the exponential-only in terms of RMSE, median, and quartile values. The best model considered the exponential and oscillatory terms, and only the loss function that penalizes the error with respect to the measured phase. Figure 3A-C shows exemplary predicted background phase maps with the best model for the testing dataset, where the error is noise-like, scales with VENC, and is more pronounced towards the edges. Figure 3D shows an inaccurate result where the phase was not accurately predicted.Discussion
In these preliminary results, the virtually equivalent performance (RMSE and distributions) between training and testing datasets suggests that the model is capable of predicting background phase without overfitting. Accuracy and precision were improved by Including oscillatory terms and a two-fold loss penalizing both the measured background phase and the fitted polynomial coefficients. However, the RMSE values are greater than the 0.6cm/s target, which warrants future improvement. Nevertheless, this criteria was established evaluating small ROIs, near isocenter, belonging to vessels. Thus, RMSE could potentially improve if we evaluate it similarly. Future work will focus on improving the model accuracy by including more slice orientations (e.g. oblique and double oblique) in the training/test datasets and potentially incorporating deep-learning techniques. Furthermore, we aim to conduct replication and in vivo experiments to further validate the approach.Conclusion
We have presented proof-of-concept for a physics-driven method to correct eddy current-induced background phase errors that shows promise in predicting and reducing these errors in 2D PC-MRI.Acknowledgements
This project was supported, in part, by U01 EB029427 to SSV and support from GE HealthCare.References
- Lankhaar JW, Hofman MB, Marcus JT, Zwanenburg JJ, Faes TJ, Vonk‐Noordegraaf A. Correction of phase offset errors in main pulmonary artery flow quantification. J Magn Reson Imag. 2005 Jul;22(1):73-9.
- Fratz S, Chung T, Greil GF, Samyn MM, Taylor AM, Buechel ER, Yoo SJ, Powell AJ. Guidelines and protocols for cardiovascular magnetic resonance in children and adults with congenital heart disease: SCMR expert consensus group on congenital heart disease. J Cardio Magn Reson. 2013 Dec 1;15(1):51.
- Gatehouse PD, Rolf MP, Graves MJ, Hofman M, Totman J, Werner B, Quest RA, Liu Y, von Spiczak J, Dieringer M, Firmin DN. Flow measurement by cardiovascular magnetic resonance: a multi-centre multi-vendor study of background phase offset errors that can compromise the accuracy of derived regurgitant or shunt flow measurements. J Cardio Magn Reson. 2010 Dec;12(1):1-8.
- Hofman M, Rodenburg MJ, Markenroth Bloch K, Werner B, Westenberg JJ, Valsangiacomo Buechel ER, Nijveldt R, Spruijt OA, Kilner PJ, Van Rossum AC, Gatehouse PD. In-vivo validation of interpolation-based phase offset correction in cardiovascular magnetic resonance flow quantification: a multi-vendor, multi-center study. J Cardio Magn Reson. 2019 Dec;21(1):1-3.
- Walker PG, Cranney GB, Scheidegger MB, Waseleski G, Pohost GM, Yoganathan AP. Semiautomated method for noise reduction and background phase error correction in MR phase velocity data. J Magn Reso Imag. 1993 May;3(3):521-30.
- Paul EA, Solana AB, Duong J, Shah AM, Lai WW, Tan ET, Hardy CJ, Chelliah A. Evaluation of self-calibrated non-linear phase-contrast correction in pediatric and congenital cardiovascular magnetic resonance imaging. Pediatr Radiol. 2020 May;50(5):656-63.
- Chernobelsky A, Shubayev O, Comeau CR, Wolff SD. Baseline correction of phase contrast images improves quantification of blood flow in the great vessels. J Cardio Magn Reson. 2007 Jan 1;9(4):681-5.
- Bernstein, M.A., King, K.F. and Zhou, X.J., 2004. Handbook of MRI pulse sequences. Elsevier.
- Magdoom, K.N., Sarntinoranont, M. and Mareci, T.H., 2020. An MRI-based switched gradient impulse response characterization method with uniform eigenmode excitation. J Magn Reson, 313, p.106720.
- Giese D, Haeberlin M, Barmet C, Pruessmann KP, Schaeffter T, Kozerke S. Analysis and correction of background velocity offsets in phase‐contrast flow measurements using magnetic field monitoring. Magn Reson Med. 2012 May;67(5):1294-302.
Figures
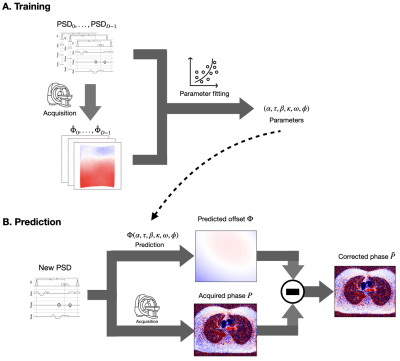
Figure 1. Method diagram. (A) Training. Training data was acquired in phantom experiments spanning a wide range of slice orientations and positions, and VENCs. Parameter fitting was performed to estimate the system-dependent parameters that characterize the system’s eddy-current impulse response. (B) Prediction. For a clinical acquisition and prospective correction, the pulse sequence information is input to the fitted model to predict the background phase offset that will be used to correct the velocity image.
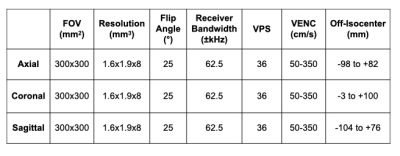
Table 1. MRI imaging parameters for the stationary phantom measurements. The VElocity ENCoding strengths (VENCs) ranged from 50-300cm/s (∆VENC=50cm/s). The TE/TR was minimized for each scan. VPS = views-per-segment.
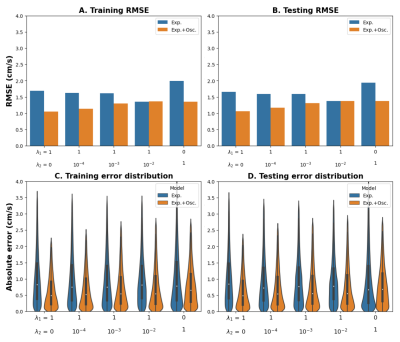
Figure 2. Quantitative assessment. (A,B) RMSE results per model tested (exponential-only vs. exponential+oscillatory) and combination of for (A) training and (B) test datasets. (C,D) Training error distribution plots (after outlier removal) for (C) training and (D) test datasets. Equivalent performances in training and testing indicate correct fitting (no overfitting). Lower RMSE, medians, and quartiles indicate better performance of the exponential+oscillatory model.
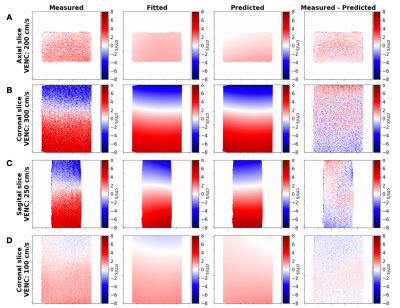
Figure 3. Qualitative assessment. Background phase offsets measured, fitted and predicted for orientations (A) axial, (B) sagittal, and (C) coronal show promising agreement. Additionally, we present an inaccurate result for a coronal slice (D).
DOI: https://doi.org/10.58530/2023/3649