Synopsis

Keywords: Phantoms, Heart, Hemodynamics, Flow, Neural network, Deep learning

Variations in velocity derivative fluctuations have been correlated with changes in pressure gradient. Image denoising and super-resolution techniques are required to accurately quantify velocity fluctuations. We propose a novel network, which we call TKE-Net to estimate Turbulent Kinetic Energy (TKE) which utilizes a ResNet convolutional neural network backbone. The network is trained and tested with low-resolution simulated CFD data, as could be derived from low resolution 4D flow in a phantom model of arterial stenosis. The results indicate good accuracy in estimating TKE. The method was also applied to in-vitro 4D flow MRI data in identical geometry.

Synopsis

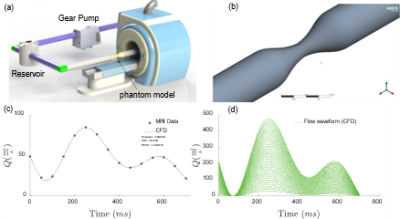
Diagnostics and prognosis of arterial stenosis require quantitative measurements of hemodynamic parameters. In particular, variations in velocity derivative fluctuations have been correlated with changes in pressure gradient. 4D flow MRI provides time-resolved 3D velocity mapping. However, image denoising and super-resolution techniques are required to accurately quantify velocity fluctuations. We propose a novel network, which we call TKE-Net to estimate Turbulent Kinetic Energy (TKE) which utilizes a ResNet convolutional neural network backbone. The network is trained and tested with low-resolution simulated CFD data, as could be derived from low-resolution 4D flow in a phantom model of arterial stenosis. The results indicate good accuracy in estimating TKE. The method was also applied to in-vitro 4D flow MRI data in identical geometry.

Introduction

The quantitative assessment of hemodynamic biomarkers plays a vital role in diagnosing and managing flow-mediated vascular diseases [1]. For example, monitoring turbulent kinetic energy along the aortic valve has shown significant promise for the assessment of the hemodynamic significance of disease [2]. Local characterization of the vortex core pattern can also assist in estimating the severity of the stenosis that requires high-resolution data [3]. 4D-flow MRI provides spatiotemporally resolved velocity vector maps of coherent blood flow in vascular structures and enables noninvasive measurement of flow parameters [4].
In this work, we focus on adapting deep learning-based super-resolution to reconstruct high-resolution turbulent kinetic energy maps directly from low-resolution 4D-flow data, leveraging prior knowledge of velocity derivative fields into high-resolution fields. This approach is advantageous to using super-resolution on 4D flow MRI directly followed with the application of numerical differentiation as super-resolution methods increase resolution only by a smaller factor (e.g., 1.5 or 2) and as a result, noise significantly dominates the calculations. For training, we generated extremely high-resolution CFD data and added Gaussian noise to ensure generalizability to realistic imaging conditions, and down-sampled these data. Using these, we trained TKE-Net to produce noise-free super-resolution TKE images with an upsampling factor of 2 when fed data with resolutions typical of 4D flow MRI. The network was trained to learn the mapping from noisy low-resolution to noise-free high-resolution TKE scalar maps. The method was further tested with CFD over a range of flow conditions and was used to predict in vitro 4D flow MRI images.

TKE-Net

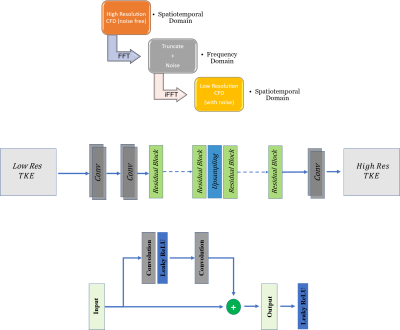
Figure 2 (a) illustrates the steps in downsampling to generate low-resolution CFD images at resolutions similar to 4D flow acquisitions. The high-resolution 2D images were blurred in the frequency domain (k-space) using the Fast Fourier Transform (FFT) of components of CFD velocities, and Gaussian noise with zero-mean and standard deviation of 0.15 was added as follows. In the frequency domain, the high frequency was removed, and the matrix size was reduced to result in a matrix with half the size along each spatial dimension. In the next step, the inverse Fast Fourier Transform (IFFT) was used to convert the k-space back to the spatial domain, resulting in low-resolution TKE images in the spatial domain.
We propose a novel TKENet using a deep convolutional neural network, residual blocks, and upsampling layer consisting of Tensorflow’s bilinear resize function. Inspired by 4D flowNet [5] which was proposed to increase resolution in 4D flow MRI data, we used eight residual blocks prior to the upsampling layer (low-resolution space) that acted as a denoiser and four residual blocks after the upsampling layer (high-resolution space) that refined the prediction. In order to prevent border artifacts, symmetric padding was applied before every convolution. Convolution layers were followed by Rectified Linear Unit (ReLU) activation functions. A sigmoid tangent activation function (tanh) was used to ensure that the output falls within the [−1,1] range. We used the Adam optimizer to learn at a rate of 10−4 mean squared error (MSE) was used for loss function. The batch size was set at 20 due to memory constraints and iterated with 500 epochs. In addition to simulations of 450 different flow conditions with CFD, the velocity data was augmented by adding Gaussian noise with standard deviation starting from 0.01 to 0.3 with a 0.01 increment to create augmented training samples. Over 12000 samples were collected, of which 80% were selected for training and 20% for testing.

Results and Discussion

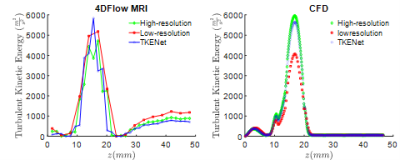
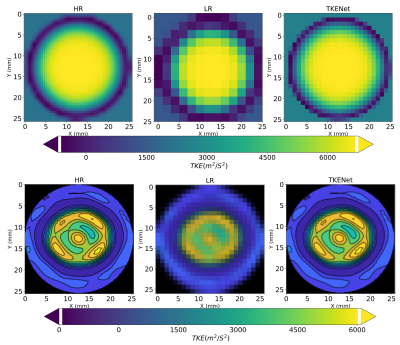
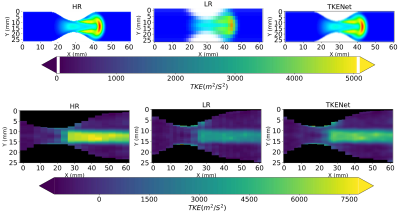
Figure 3 shows the spatial averaged turbulent kinetic energy in x and y directions at peak systolic time. High-resolution CFD was considered as the ground truth reference. While the TKE in low resolution follows a similar pattern as high resolution, the TKE-Net captures the peak TKE value around the stenosis. A similar trend was also observed for 4D flow MRI. Figure 4 shows a comparison of synthetic 4D flow TKE images with ground truth as CFD 4D flow MRI TKE images with upsampling factor of 2. There was good agreement between TKE-Net predictions and the CFD, as well as the 4D flow MRI acquisitions for the stenotic phantom. Figures 4 presents the performance of the TKE net in a mid-axial plane for CFD data. Note the detailed structure of TKE profile depicted for CFD due to the extremely highresolution of the data compared with 4D flow MRI.

Acknowledgements

This work was supported by National Institute of Health with contract Grant Number: 5R21HL132263.