3615
A deep learning method for diffusion tensor imaging using spherical harmonic representation1School of Biomedical Engineering, Southern Medical University, Guangzhou, China
Synopsis
Keywords: Machine Learning/Artificial Intelligence, Diffusion Tensor Imaging
Deep learning methods have been demonstrated state-of-the-art performance in Diffusion Magnetic Resonance Imaging (dMRI) denoising and parameter estimation. However, existing deep learning methods for dMRI are limited to the specific acquisition scheme. To solve the limitation, we proposed to use spherical harmonic coefficients as the deep learning network’s input. Our results have shown that the proposed method has a high performance in denoising and parameter estimation for DTI with a strong generalization ability.Introduction
The diffusion tensor imaging (DTI) can map the diffusion process of water molecular within biological tissues and noninvasively visualize white matter fibers by acquiring at least one non-diffusion-weighted image and six diffusion-weighted (DW) images. DTI have been widely used in neuroscience. However, the DW images have low signal-to-noise ratio (SNR) due to the diffusion weighting and long echo time. The high noise level will affect the accuracy of DTI parameter estimation. The deep learning has shown excellent performance in dMRI denoising and parameter estimation. Nevertheless, existing deep learning-based methods used dMRI data with single acquisition scheme as train data of convolutional neural network (CNN)1-3, and could not be applicable to new acquisition scheme (different b value and/or diffusion gradient scheme). The spherical harmonic coefficients are invariable for the same diffusion signal profile not relevant to the acquisition scheme. Inspired by this, we use the spherical harmonic coefficient as the input of the neural network to predict DTI tensor.Theory
DW signal normalizationTo obtain diffusion signal profile and eliminate the influence of b value, we firstly transform the DW signal as follows:
$$s=(\frac{s_{b}}{s_{0}})^{\frac{b_{train}}{b}}$$
where $$$s_0$$$ is the non-diffusion-weighted signal, $$$s_b$$$ is the DW signal with b value = b mm/s2, $$$b_{train}$$$ is the b value of the training data. In our method, the normalized DW signals with different diffusion directions is combined into a spherical signal for each voxel. Then the spherical signal is used to obtain spherical harmonic coefficients.
Spherical harmonic representation
An integrable spherical signal $$$s$$$ can be linearly represented by spherical harmonic basis elements4.
$$s(x)=\sum_{l=0}^{B}\sum_{m=-l}^{m=l}\hat{s}_{l}^{m}Y_{l}^{m}(x)$$
where $$$x\in R^{3}$$$ is the unit vector, $$$Y_{l}^{m}$$$ is the spherical harmonic basis element of degree $$$l$$$ and order $$$m$$$, $$$\hat{s}_{l}^{m}$$$ is the spherical harmonic coefficient of degree $$$l$$$ and order $$$m$$$.
The spherical harmonic coefficient $$$s ̂_l^m$$$ can be obtained by
$$\hat{s}_{l}^{m}=\int_{S^{2}}^{}s(x)Y_{l}^{m*}(x)dx$$
where $$$S^2$$$ is unit sphere with a set of points $$$x$$$. $$$Y_{l}^{m*}$$$ is the inverted spherical harmonic basis of degree $$$l$$$ and order $$$m$$$.
Methods
The flow diagram of the proposed method is displayed in Fig. 1.We perform DW signal normalization (step 1) and Spherical harmonic representation (degree $$$B$$$ = 2) (step 2) for the dMRI data from any acquisition scheme to obtain spherical harmonic coefficients. Then spherical harmonic coefficients are fed into the network to obtain DTI tensor field.Network
We use a 3D U-net5 (see Fig. 2), consisting of 3D convolution layer, maxpooling layer, upsampling layer and skip connection layer. The network’s loss function as follows:
$$L=MSE(\frac{S_{b}^{truth}}{S_{0}^{truth}}-e^{-bg\hat{D}g^{T}}) $$
where the $$$\hat{D}$$$ represents the DTI tensor field predicted by the proposed method, g represents the diffusion direction of the train data. $$$S_{b}^{truth}$$$ represents the noise-free DW images, and $$$S_{0}^{truth}$$$ represents the noise-free non-diffusion-weighted image.
Simulated data pre-processing
The dMRI datasets of 24 subjects (16 for training, four for validation, four for testing) are from MGH-USC HCP6. For each subject, only five b = 0 mm/s2 and 64 b = 1000 mm/s2 volumes were used in this study. We use MRtrix7 to process the dMRI datasets, including denoising, Gibbs artifact removal and bias field correction. Then the DTI tensor field was estimated using weighted linear least squares (WLLS)8 method. The DTI tensor field was used to reconstruct the dMRI data in one b = 0 mm/s2 volume and 15 b = 1000 mm/s2 volumes. The reconstructed dMRI data was used to obtained ground truth. We add Rician noise into each subject’s reconstructed dMRI data. The noise levels range from 0.01 to 0.03. Finally, the noisy dMRI data was used to obtain spherical harmonic coefficients.
Experiments
To demonstrate the proposed method is robust to the different acquisition schemes, we designed two experiments. In first experiment, we compared the proposed method (spherical harmonic coefficients as the network’s input) with the regular U-net (dMRI data as the network’s input) and MPPCA9. One dMRI data (the diffusion directions are different from the training data) is used for testing three mothods. In the second experiment, we use a real high-resolution dMRI data (0.9 mm isotropic voxel size) with one b = 0 mm/s2 volume and 12 b = 800 mm/s2 volumes to test. For comparison, we use MPPCA to denoise the data and use WLLS to estimate DTI tensor field.Results
In Fig.3, the dMRI data’s diffusion gradient scheme is different from the training data. The six element maps of DTI field obtained in proposed method are less noisy with more accurate details preserved and have the lowest RMSE. In Fig 4, the real dMRI data’s acquisition scheme is different from the train data. Compared with MPPCA, FA and MD obtained in proposed method are less noisy. Both results prove that this method has a strong generalization ability.Discussion and conclusion
Our method utilize the spherical harmonic coefficient as the input of the neural network, is suitable to different acquisition schemes for diffusion tensor imaging and has shown a high performance in denoising and parameter estimation for DTI. In clinical application, as long as we know the b value and diffusion direction of dMRI data, we can use the trained model accurately estimate the DTI tensor field.Acknowledgements
This study was supported by the National Natural Science Foundation of China under Grant 61971214.References
1. Aliotta E, Nourzadeh H, Sanders J, Muller D, Ennis DB. Highly accelerated, model-free diffusion tensor MRI reconstruction using neural networks. Med Phys 2019;46(4):1581-1591.
2. Tian Q, Bilgic B, Fan Q, et al. DeepDTI: High-fidelity six-direction diffusion tensor imaging using deep learning. Neuroimage 2020;219:117017.
3. Li Z et al. Fast and Robust Diffusion Kurtosis Parametric Mapping Using a Three-Dimensional Convolutional Neural Network. IEEE Access 7, 71398–71411 (2019).
4. Sedlar S, Alimi A, Papadopoulo T, Deriche R & Deslauriers-Gauthier S. A Spherical Convolutional Neural Network for White Matter Structure Imaging via dMRI. in Medical Image Computing and Computer Assisted Intervention – MICCAI 2021 (eds. de Bruijne, M. et al.) vol. 12903 529–539 (Springer International Publishing, 2021).
5. Çiçek Ö, Abdulkadir A, Lienkamp SS, Brox T, Ronneberger O. 3D U-Net: Learning Dense Volumetric Segmentation from Sparse Annotation. Medical Image Computing and Computer-Assisted Intervention – MICCAI 2016. Cham: Springer International Publishing; 2016. p. 424-432.
6. Setsompop K et al. Pushing the limits of in vivo diffusion MRI for the Human Connectome Project. NeuroImage 80, 220–233 (2013).
7. Tournier JD, Smith R, Raffelt D, et al. MRtrix3: A fast, flexible and open software framework for medical image processing and visualisation. Neuroimage 2019;202:116137.
8. Veraart J, Sijbers J, Sunaert S, Leemans A & Jeurissen B. Weighted linear least squares estimation of diffusion MRI parameters: Strengths, limitations, and pitfalls. NeuroImage 81, 335–346 (2013).
9. Veraart J, Novikov DS, Christiaens D, Ades-Aron B, Sijbers J, Fieremans E. Denoising of diffusion MRI using random matrix theory. Neuroimage 2016;142:394-406.
Figures

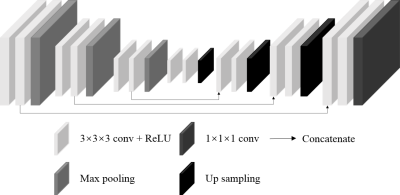
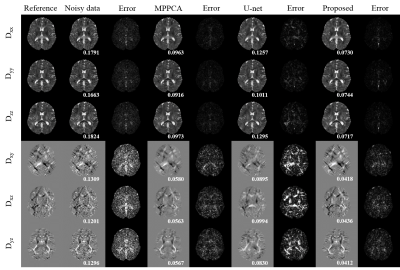
Fig.3 The six element maps of DTI tensor field obtained from different methods and corresponding error maps. The dMRI data has one b = 0 mm/s2 volume and six b = 1000 mm/s2 volumes with noise level of 0.01. The DTI tensor field of MPPCA was estimated from corresponding denoised dMRI data. The U-net represents a 3D U-net which used dMRI data as train data. The RMSE is shown in the bottom of each element.
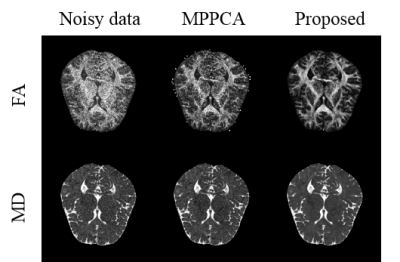
Fig.4 FA and MD obtained from different methods. The real data has one b = 0 mm/s2 volume and 12 b = 800 mm/s2 volumes. The FA and MD of MPPCA were estimated from corresponding denoised dMRI data.