3612
Orthogonal diffusion encoding gradient sequence (ODEG) improves time-dependency measurements in the human brain1zhejiang University, Hangzhou, China, 2Siemens Healthcare China, Shanghai, China
Synopsis
Keywords: Pulse Sequence Design, Diffusion/other diffusion imaging techniques
Oscillatory gradient dMRI is used to access restricted diffusion at short diffusion times (td). But its clinical application is limited due to the limited gradient strength, leading low b-value and low resolution, and thus is subject to contamination from microcirculation and CSF partial volume. Here we proposed an orthogonal diffusion encoding gradient (ODEG) sequence to improve td–dependency measurements in human brain, by applying a pulse gradient orthogonal to the oscillating gradient to suppress the fast diffusion from microcirculation and free water. The results showed that td-dependency was significantly improved by the ODEG sequence in the hippocampus and cortical gray matter.
Introduction
Oscillatory gradient (OG) [1] diffusion MRI (dMRI) is used to access short diffusion times (td), which is used in combination with pulse gradient (PG) to characterize tissue microstructures[2-5] at varying tds. OG-dMRI requires high gradient strength to achieve sufficient b-value, which is difficult on clinical systems. dMRI measurement at low b-value is known to be affected by the microcirculatory flow [6,7], and may affect the td-dependency measurement. In addition, tissues in the vicinity of the ventricles and sulci could be disturbed by CSF due to partial volume effect and point spread functions[8,9] at low resolution.The present study[10] proposed an orthogonal diffusion encoding (ODEG) method that applied a small pulsed gradient orthogonal to oscillating gradient to suppress the interference of microcirculation and CSF on td-dependent measurements. We tested the td dependence in several GM and WM regions of the human brain on a 3T Siemens machine using the proposed ODEG sequence, which was compared with the conventional OGSE sequence.
Methods
Pulse sequence: The ODEG sequence, shown in Figure 1, consists of three modules: the fat saturation module, the diffusion weighting module, and the EPI readout module. The diffusion weighting modules contains a pair of cosine-trapezoid oscillating gradient (DG1) and pulse gradient (DG2) applied in orthogonal directions. As proved in our previous study [10], two gradients applied in orthogonal directions do not interfere with each other in the power spectrum, and their b-values can be directly added. In this sequence setup, a low PG is applied in both b0 and DWI images to suppress the microcirculation and CSF component.Data acquisition: MRI scans were performed on a 3T Siemens Prisma scanner with a 64-channel head coil. The phantom data were acquired with a PG-encoding (△eff = 50ms, 0Hz) and OG-encodings at frequencies of 20 Hz and 40 Hz, with bDG1 = 200 s/mm2. The DG2 in the ODEG was set at bDG2 = 200 s/mm2 as a baseline. The in vivo data were acquired at frequencies of 20 Hz, 40 Hz, and 60 Hz (effective td = 25, 12.5, and 8.34 ms), with bDG1 = 400 s/mm2. The DG2 in the ODEG was set at bDG2 = 400 s/mm2 as a baseline. The other parameters included: FOV = 220 × 200 mm2, voxel size = 2 × 2 × 4 mm3, TR/ TE = 5100/130 ms, NEPI = 100, 6 diffusion directions with two averages, bDG2 (pseudo b0) with 4 averages, GRAPPA accelerated factor = 2, partial Fourier factor = 6/8.
Data analysis: Regions of interest (ROIs) including the hippocampus, subcortical white matter (WM), cortical gray matter (GM), thalamus, and splenium of the corpus callosum (SCC) were manually delineated (Figure 2). The ADC of ODEG was calculated as ADC = -log(SDG1+DG2/SDG2)/bDG1. The variations in ADC between different tds were evaluated by ANOVA followed by post-hoc t-tests with Bonferroni correction. In addition, we estimated the apparent diffusion dispersion rate (Λ) and exponent (θ) based on the diffusion dispersion model: Dω = Dω0 + Λωθ[3,8,9].
Results
The ODEG sequence was first tested in a water phantom, which showed no difference between PG and OG encoding at different oscillating frequencies (Figure 2). Figure 3 shows ADC maps of a volunteer brain acquired at different oscillating frequencies, which indicated the high ADC in the sulcal regions were suppressed using the ODEG sequence compared to conventional OGSE. Pairwise comparisons of ADC at different tds were summarized in Figure 4. Overall, the td-dependency of ADC was stronger using ODEG than OGSE in almost all ROIs. Specifically, no significant td-dependency was observed in the hippocampus and cortical GM using OGSE; and in the thalamus, subcortical WM regions, and SCC, OGSE-based ADC differences were only detectable between OG and PG scans, but not between different OG frequencies. In contrast, the ADC differences were significant between all tds in all ROIs using the ODEG sequences. Besides, due to the suppression of the high diffusion of CSF and microcirculation, the ADC measured by ODEG sequence was significantly lower than that of OGSE sequence (p< 0.001) for the whole-brain.The diffusion dispersion curves and fitted power-law equations with parameters Λ and θ were displayed in Figure 5. We found θ was the highest in thalamus and SCC, followed by the subcortical WM and hippocampus, and cortical GM exhibited the lowest θ using ODGE measurement.
Discussion and Conclusion
In this work, we proposed an orthogonal diffusion encoding gradient sequence (ODEG) to investigate td-dependent diffusivity in the human brain. Compared with the conventional OGSE sequence, the proposed sequence with a baseline pulsed gradient orthogonal to the main gradient to suppress the CSF and microcirculation signal, and therefore improve the td-dependency measurements, especially in the tissue surrounding the ventricles and sulci. A limitation of the proposed sequence is that the use of an additional diffusion gradient reduced the maximum available gradient strength and also SNR of the acquired images.Acknowledgements
This work was supported by the Ministry of Science and Technology of the People’s Republic of China (2018YFE0114600), the National Natural Science Foundation of China (61801424, 81971606, 82122032, 2021ZD0200202), and the Science and Technology Department of Zhejiang Province (202006140, 2022C03057).
References
1. Does MD, Parsons EC, Gore JC. Oscillating gradient measurements of water diffusion in normal and globally ischemic rat brain. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 2003;49(2):206-215.
2. Drobnjak I, Zhang H, Ianuş A, et al. PGSE, OGSE, and sensitivity to axon diameter in diffusion MRI: insight from a simulation study. Magnetic resonance in medicine 2016;75(2):688-700.
3. Novikov DS, Jensen JH, Helpern JA, et al. Revealing mesoscopic structural universality with diffusion. Proceedings of the National Academy of Sciences 2014;111(14):5088-5093.
4. Novikov DS, Kiselev VG. Surface-to-volume ratio with oscillating gradients. Journal of magnetic resonance 2011;210(1):141-145.
5. Xu J, Li H, Harkins KD, et al. Mapping mean axon diameter and axonal volume fraction by MRI using temporal diffusion spectroscopy. NeuroImage 2014;103:10-19.
6. PANAGIOTAKI E, WALKER-SAMUEL S, SIOW B, et al. Noninvasive quantification of solid tumor microstructure using VERDICT MRI. Cancer Res 2014, 74(7): 1902-12.
7. WETSCHEREK A, STIELTJES B, LAUN F B J M R I M. Flow‐compensated intravoxel incoherent motion diffusion imaging. Magnetic resonance in medicine 2015, 74(2): 410-9.
8. LI H, ZU T, HSU Y C, et al. Inversion‐Recovery‐Prepared Oscillating Gradient Sequence Improves Diffusion‐Time Dependency Measurements in the Human Brain. 2022,
9. Michael E, Hennel F, Pruessmann K, et al. Evaluating diffusion dispersion across an extended range of b‐values and frequencies: Exploiting gap‐filled OGSE shapes, strong gradients, and spiral readouts. Magnetic resonance in medicine 2022, 87(6): 2710-23.
10. WU D, MORI S. Structural Neuroimaging: From Macroscopic to Microscopic Scales. Handbook of Neuroengineering 2022, 1-35.
Figures
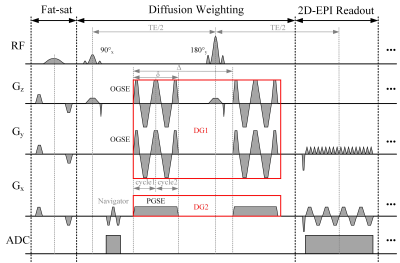
Figure 1: Diagram of the orthogonal diffusion encoding gradient sequence (ODEG) sequence. In the diffusion weighting module, a pair of orthogonally applied trapezoid-cosine oscillating gradient (DG1) and pulsed gradient (DG2) was inserted in the 90°x −180°y −90°−x RF pulses.

Figure 2: b200 images obtained from ODEG and OGSE sequences at 40Hz. The DG2 in the ODEG was set at b = 200 s/mm2 as a baseline. ADC obtained from ODEG and OGSE sequences at different oscillating frequencies showed no significant difference.

Figure 3: b0 and ADC maps obtained from ODEG and OGSE sequences at different oscillating frequencies. Regions-of-interest (ROIs) are delineated, including the hippocampus, subcortical WM (green), cortical GM (blue), thalamus (cyan), and SCC (purple).
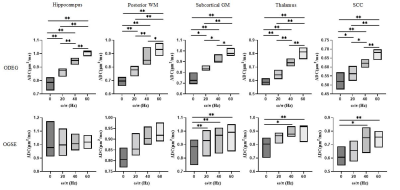
Figure 4: Diffusion-time (td) dependent ADC measured using the ODEG and OGSE sequences at different frequencies (0Hz, 20Hz, 40Hz, 60Hz). Using the ODEG sequence, all ROIs showed td-dependent changes of ADC between all tds. In comparison, using the OGSE sequence, the td-dependent effect was not observable in regions close to the ventricle and sulci, including the hippocampus and cortical gray matter. (*p < .05 and **p < .01 by post-hoc t-test)
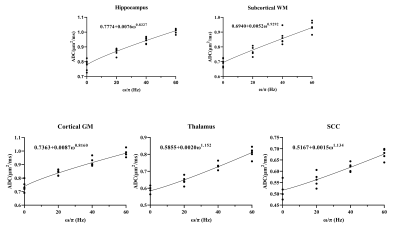
Figure 5: td-dependent ADC values measured from the ODEG sequence at different frequencies (60Hz, 40Hz, 20Hz, and 0Hz) were fitted according to a power-law function (Dω = Dω0 + Λωθ). The diffusion dispersion exponent θ was the highest in thalamus and SCC, followed by the subcortical WM, and hippocampus, and cortical GM exhibited the lowest θ using ODGE measurement.