Synopsis

Keywords: Image Reconstruction, Diffusion/other diffusion imaging techniques, q-space, denoising

DISCUS addresses two challenges currently limiting the analysis potential of diffusion MRI: sparsity of measurements and variability in q-space sampling schemes. Our method combines the advantages of model-fit approaches with continuous sampling (spherical harmonics, SHORE) and rigid, discrete learning-based methods. DISCUS can be initialized from any acquisition scheme and permits signal prediction for an arbitrary q-vector. Despite the added flexibility, DISCUS performs on par with other, far less flexible learning methods, while outperforming model-fit methods. DISCUS-derived signals translate to higher-quality FA estimates promising accurate analyses even from very short acquisitions.

Introduction

Two of the key factors limiting the diagnostic and analysis potential of diffusion MRI are that (1) q-space can only be sampled sparsely due to constraints on acquisition time; and (2) q-space sampling schemes vary widely across studies, making it challenging to combine datasets. The latter could be addressed by continuous modeling of q-space or propagators, e.g. with spherical harmonics¹ (SH) or SHORE², but these approaches often yield poor results when q-space data are sparsely sampled and noisy. Learning-based reconstruction methods³ may substantially outperform modeling approaches, but they are constrained to the fixed sampling scheme of the training data. Combining the advantages of the model- and learning-based reconstruction methods, we present the first end-to-end learning-based method for continuous diffusion MRI signal reconstruction: Diffusion MRI Signal Reconstruction with Continuous Sampling (DISCUS).

Methods

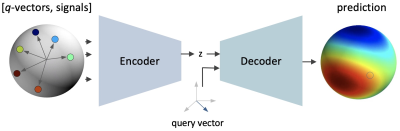
Given N observations, which are pairs of q-vectors and acquired, spatially aligned, diffusion-weighted images (DWIs), we aim to reconstruct a DWI for an arbitrary, unseen q-vector (query vector). Here, reconstruction at each spatial location (voxel) is treated as an independent task (in line with other methods, e.g., SH and SHORE). Our deep learning model features an encoder and decoder specifically designed for this task (see Figure 1). At each voxel, the encoder receives the observation (N tuples of q-vectors and acquired signals) and outputs a vector summarizing the information across measurements. The decoder accepts a query vector as input and predicts the corresponding signal based on the summary vector of the encoder. During training, we augment the acquired data by building random subsets supplying the deep learning model with a variety of observations for reconstruction. The mean squared error between model predictions and acquired signals guides parameter updates during training. For model performance evaluation, we obtain approximately uniformly distributed samplings containing N=10, 20, 30, and 50 vectors for observation and one test sampling containing 30 query vectors. We initialize the model with the respective observation set, obtain predictions for the 30 query vectors, quantify the agreement with withheld reference signals via normalized squared error, and report error distributions over all white and gray matter voxels.

Results

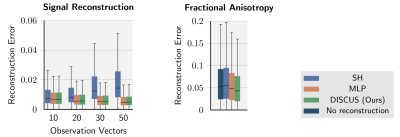
We build training, validation, and test datasets using single-shell diffusion data from the Human Connectome Project. As reference methods, we choose a least-squares fit of SH via Mrtrix⁴ and we adapt an MLP³ for signal reconstruction. We compare reconstruction methods across different observations in Figure 2 (left). For larger observations, the reconstruction error decreases for the two learning-based methods MLP and DISCUS and increases for the SH method. For all observations, the reconstruction error of the SH method is considerably larger compared to the learning-based methods (MLP and DISCUS), which have almost equal error distributions. Furthermore, in Figure 2 (right), we compare fractional anisotropy⁵ (FA) estimation from the respective reconstructions, using 10 observation measurements for all methods. Here, the learning-based MLP and DISCUS methods outperform the SH method and DISCUS performs best. Both learning-based methods also outperform the FA estimate that we obtain by fitting a tensor directly on the original 10 measurements, without inferring signals at additional q-space locations.

Discussion

The results indicate that learning-based methods can reconstruct signals with high accuracy and that the MLP and DISCUS methods yield predictions of similar quality (Figure 2, left). The higher prediction accuracy of learning-based approaches translates into FA estimates more in line with the acquired data (Figure 2, right). In contrast to the MLP, which does not assume knowledge of the q-vectors and is therefore agnostic to the geometric relationship between signal samples, our model explicitly models the signal on continuous q-space. This seems to benefit the estimation of summary descriptors such as FA. In this work, we construct the q-space signal independently at each spatial location taking only information from the particular voxel into account. We conjecture that incorporating spatial information, e.g. from neighboring voxels, benefits the reconstruction task especially when only little directional information is available, e.g. in very sparse acquisitions.

Conclusion

Our DISCUS method extends existing learning-based methods in two ways. While learning-based methods have, thus far, been restricted to accepting only signals corresponding to the specific q-space sampling scheme of the training data, our method has no such limitation and can be initialized from any acquisition scheme. Similarly, learning-based methods have, so far, been restricted to only predicting signals for the specific q-space sampling scheme of the training data whereas our method permits flexible signal query at any q-space location. This method addresses the limitations imposed by the sparsity of measurements and variability in q-space sampling schemes. Our method permits faithful reconstruction of the signal at any q-vector from a small number of q-space measurements, allowing accurate analyses even for very short acquisitions. Furthermore, the flexible reconstruction of arbitrary query vectors from any acquisition scheme may be used for data harmonization, by resampling data acquired with different, sparse q-space sampling schemes onto a common set of q-space locations.

Acknowledgements

No acknowledgement found.