Synopsis

Keywords: Image Reconstruction, Diffusion/other diffusion imaging techniques, Diffusion Acquisition & Reconstruction

3D multi-shot multi-slab imaging can provide superior SNR efficiency for high-resolution dMRI but suffers from motion-induced shot-to-shot phase variations. We propose a highly-efficient, self-navigated method to correct for phase variations in 3D multi-slab dMRI. The sampling of each shot is designed to intersect with the kz=0 plane. These intersections are used to reconstruct a 2D phase map for each shot using a structured low-rank reconstruction that leverages the redundancy in shot and coil dimensions. The phase maps are used to eliminate the phase inconsistency in the final 3D multi-shot reconstruction. We demonstrate the method’s efficacy using highly realistic simulations.

Introduction

High-resolution diffusion MRI (dMRI) can non-invasively estimate white matter fiber architecture in in-vivo human brains. The intrinsically limited SNR is one of the major barriers to its wider adoption for neuroscientific and clinical applications. This can be potentially addressed using 3D multi-slab imaging, which can achieve optimal SNR efficiency for spin-echo based dMRI due to its compatibility with TR=1-2s^1,2.

3D multi-shot EPI is the typical method to facilitate 3D multi-slab imaging. However, as all multi-shot dMRI acquisitions, it suffers from motion-induced shot-to-shot phase variations which create artifacts that substantially compromise image reconstruction and analysis. Phase errors are conventionally measured using a navigator acquired after the imaging echo and corrected as part of the multi-shot image reconstruction. 2D navigators are sufficient for thin slabs (i.e., <30 mm)^1-3. Nevertheless, navigator acquisition prolongs the acquisition time by 25%-50%^2,3 and increases the SAR, which is particularly problematic for high-field imaging.

We propose a novel 3D sampling and associated structured low-rank (SLR) based reconstruction to eliminate the need for navigator acquisition to achieve high-resolution dMRI with better time efficiency. The proposed method is demonstrated using highly realistic simulations based on retrospectively re-sampled in-vivo data.

Methods

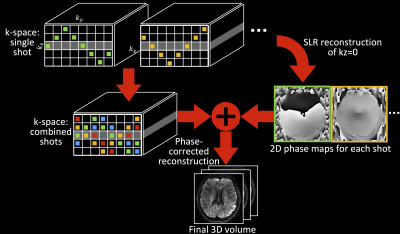
The overview of the proposed method is demonstrated in Fig.1. In summary, each shot is designed to cover a wide range in the slice direction (kz) and intersect with the central kz plane (kz=0). These intersections are used to reconstruct the kz=0 plane for each shot using a SLR based reconstruction. The resulting image provides a 2D phase image similar to a navigator (but with no additional scan time), which is then incorporated into the multi-shot reconstruction to eliminate the shot-to-shot phase-inconsistency⁴.

Sampling pattern design
The sampling adapts blipped-CAIPI⁵ following several design principles:
1) Each shot intersects with the kz=0 plane to provide self-navigation points.
2) The overlap between different shots is minimized to reduce redundancy.
3) The aggregate sampling across shots minimizes gaps and maximizes uniformity.
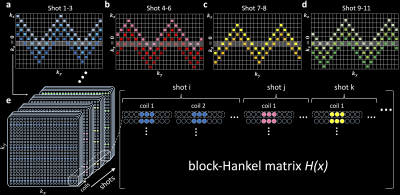
The resultant sampling patterns are showed in Fig.2a-d. The base sampling for one shot (e.g., Fig.2a, light blue) is entitled an “extended blipped-CAIPI” trajectory. Most shots are variants of this trajectory, supplemented with one additional shot without kz blips to only cover kz=0. The latter shot produces an accurate estimation of kz=0 magnitude image and aims to benefit the SLR reconstruction which enforces the similarity between the underlying magnitude images from different shots⁶. The acquisition time is equal to a conventional 3D multi-slab sampling¹ without explicitly-acquired navigators.

Image reconstruction
The reconstruction includes two steps:
1) Reconstruct kz=0 for different shots to obtain a 2D phase estimate for each shot.
2) Incorporate the shot phase into multi-shot reconstruction to eliminate the shot-to-shot phase variance.
Due to limited intersections with kz=0 for each shot (Fig.2a-d), step 1 reconstruction is highly under-sampled (R=18-36). We address this extreme under-sampling by jointly leveraging the shared information across shots and coils⁷ using a SPIRiT⁸-SLR reconstruction:
$$x_{k_z=0}=\text{arg}\min_x\left|\left|D_{k_z=0}x-y_{k_z=0}\right|\right|_2^2+\lambda_1\left|\left|(G_{k_z=0}-I)x\right|\right|_2^2+\lambda_2\left| \left|H(x)\right|\right|_*.\quad\quad(1)$$
Here, x is the target multi-coil k-space data, D is the under-sampling operation, y is the acquired multi-coil data, G is the SPIRiT kernel, and H(x) is the block-Hankel matrix generated from x (Fig.2e). The 2D phase maps P for different shots are extracted from the reconstructed, 2D Gaussian kernel-filtered kz=0 images.

The phase maps P are then incorporated into a phase-corrected 3D multi-shot reconstruction:
$$x_{slab}=\text{arg}\min_x\left|\left|D_{slab}FPF^{-1}x-y_{slab}\right|\right|_2^2+\lambda_3\left|\left|(G_{slab}-I)x\right|\right|_2^2,\quad\quad(2)$$
where F is the Fourier transform.

To evaluate the efficacy of leveraging the low-rankness along the coil dimension, a SENSE-based SLR⁶ was also implemented with SLR constraints only in the shot dimension:
$$x_{k_z=0}=\text{arg}\min_x\left|\left|D_{k_z=0}FSF^{-1}x-y_{k_z=0}\right|\right|_2^2+\lambda_4\left|\left|H(x)\right|\right|_*.\quad\quad(3)$$
Here, x is the coil-combined k-space data, and S is the sensitivity maps.

For comparison, the kz=0 reconstruction from SENSE-SLR was also filtered and phase-extracted for the reconstruction in Equation (2).

Equation (1) was solved with the alternating direction method of multipliers (ADMM)⁹. The kernel size for SPIRiT and Hankel matrix construction was 5×5. λ₁/λ₂/λ₃/λ₄=1/10^-5/1/10^-5. Reconstruction performance was evaluated using normalized root mean squared error (NRMSE).

Retrospective simulation
We performed realistic simulations on a single-slab, navigated dMRI dataset acquired at 7T. Acquisition parameters: 1.22mm isotropic resolution, 12 slices, TE1(imaging)/TE2(2D navigator)/TR=72/128/1800ms, b=1000s/mm², Ry/Rz=3/1. Fully-sampled reference data were obtained from three scans with 0, 1, and 2∆ky shift. Phase-corrupted multi-shot data were generated by multiplying the reference data with navigator phase maps before applying the shot sampling masks.

Results

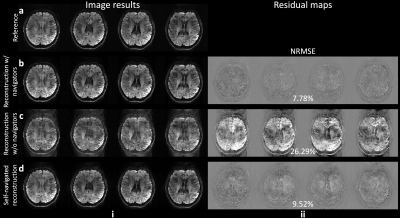
Figure 3 demonstrates the SPIRiT-SLR estimated phase maps, which have high similarity to the reference phase maps acquired by the navigators (Fig.3a-b). The filtering further reduces the residual artifacts (Fig.3c).

The multi-shot image reconstruction results are shown in Fig.4. The motion-induced phase variance results in severe image artifacts if uncorrected (Fig.4c, NRMSE: 26.29%). The proposed self-navigated method substantially reduces the artifacts (Fig.4d) and produces similar results to the reconstruction with explicitly-acquired phase navigators (Fig.4b, NRMSE: 9.52% vs. 7.78%).

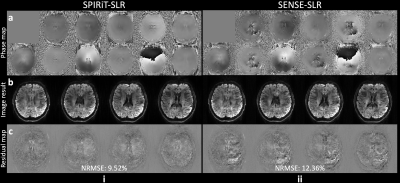
Compared to the SENSE-SLR, the proposed SPIRiT-SLR benefits from the utilization of low-rankness in the coil dimension. This is reflected in higher quality phase map estimations (Fig.5a). The whole-slab image reconstruction using SPIRiT-SLR estimated phase maps produces more accurate images with lower NRMSE (Fig.5b-c, 9.52% vs. 12.36%).

Discussion and Conclusion

The proposed method eliminates the needs for the navigator acquisition in 3D multi-slab imaging to achieve high-resolution 3D dMRI with better time-efficiency.

Acknowledgements

W.W. is supported by the Royal Academy of Engineering (RF\201819\18\92). K.L.M. is supported by the Wellcome Trust (WT202788/Z/16/A). M.C. is supported by the Canada Research Chair Program. The Wellcome Centre for Integrative Neuroimaging is supported by core funding from the Wellcome Trust (203139/Z/16/Z).