Introduction

Diffusion MRI (dMRI)¹ is widely used to study the tissue microstructure noninvasively but suffers from long acquisition time. Simultaneous multi-slice imaging (SMS)^2-3 with in-plane undersampling has been proposed to accelerate the acquisition time while minimizing the TE. However, image reconstruction typically suffers from inter-slice leakages and in-plane aliasing artifacts as the acceleration factor increases. Furthermore, aliasing separation at the high b-value becomes more challenging because a single-band b=0 calibration scan is typically acquired for kernel training and hence discrepancies between calibration and imaging exist. To address them, we propose a novel, k-space-based one-step solution reconstruction for ultra-fast whole-brain diffusion MR acquisition with generalized self-calibrating SMS MR image reconstruction⁴, which optimally exploits a measured SMS 3D k-space with additional calibrating signals from generalized 3D Fourier encoding perspective. Experimental studies are performed to validate the effectiveness of the proposed method.

Methods

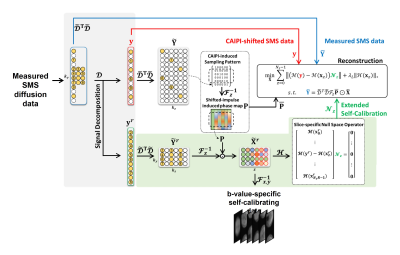
Forward SMS Signal Model for diffusion MRI: With the CAIPI condition, a measured SMS signal for each diffusion MR data can be expressed by:
$$\mathbf{Y} = \mathcal{D}^{T} \mathcal{D} \mathcal{F}_z \left(\mathbf{\overline{P}} \odot \mathbf{X}\right) + \mathbf{N}$$
where $$$\mathcal{D}$$$ is the operator selecting and vectorizing measured signals; $$$\mathcal{D}^T$$$ is the operator getting them back to the original sampling position; $$$\mathbf{\overline{P}}$$$ is the CAIPI-demodulated phase matrix; $\odot$ is the Hadamard product (element-wise matrix multiplication); $$$\mathbf{N}$$$ is the noise matrix; $$$\mathbf{y}$$$ is the measured signal vector in $$$k$$$ space.
In the presence of in-plane undersampling, extended controlled aliasing is performed by upsampling the measured data in the k_z-direction to jointly resolve both inter-slice leakages and in-plane artifacts in a single step. In-plane aliased images are replaced with a concatenation of these aliasing-free images along the slice direction. Additionally, this is simply equivalent to upsampling with zero insertions in 3D k-space. For self-calibration, the measured SMS data with self-calibrating is decomposed into two sets of data for under-sampled SMS imaging data and fully sampled calibration data. A slice-specific null space operator is then learned using extended self-calibration that exploits target slices and corresponding in-plane-shifted images.

One-step k-space-based Reconstruction for Undersampled SMS Imaging: To jointly resolve slice separation and in-plane aliasing artifacts in a single step, image reconstruction with the upsampled SMS imaging data is formulated as a constrained optimization problem. We propose an integrated objective function with null space reconstruction consistency, Hankel-structured low rank prior, and data fidelity from 3D Fourier space:
$$\mathcal{J}\left(\mathbf{\tilde{X}}=\left(\mathbf{x}_{0}, \cdots, \mathbf{x}_{N_\mathrm{s}-1}\right)\right)={\sum_{z=0}^{N_\mathrm{s} -1}} \frac{1}{2}\parallel { ( \mathcal{H} ( \mathbf{y} )-\mathcal{H} ( \textbf{x}_{z} ) ) \mathcal{N}_z}_{F}\parallel^{2}+ \lambda_L \parallel{\mathcal{H} \left( \mathbf{x}_{z} \right) }\parallel_{*}\\ s.t. \quad \mathbf{\tilde{Y}} = \mathcal{\tilde{D}}^{T} \mathcal{\tilde{D}} \mathcal{F}_z (\mathbf{\overline{P}} \odot \mathbf{\tilde{X}})$$
where $$$\mathbf{\tilde{X}}$$$ denotes the extended set of unknowns, CAIPI-modulated diffusion-weighted images and their shifted replica; $$$\parallel { ( \mathcal{H} ( \mathbf{y} )-\mathcal{H} ( \textbf{x}_{z}) ) \mathcal{N}_z}_{F} \parallel^{2}$$$ represents null space reconstruction consistency that controls signal passing in a slice of interest and signal nulling in its outer slices; $$$F$$$ is the Frobenius norm; $$$\lambda_L$$$ is the regularization parameter; $$$\parallel{\mathcal{H} \left( \mathbf{x}_{z} \right ) }\parallel_*$$$ is the Hankel-structured low rank prior; $$$\mathbf{\tilde{Y}} = \mathcal{\tilde{D}}^{T} \mathcal{\tilde{D}} \mathcal{F}_z (\mathbf{\overline{P}} \odot \mathbf{\tilde{X}}) $$$ represents the data fidelity that enforces measured signals in $$$\mathbf{k}$$$-$$$k_z$$$ space; Hence, $$$\mathbf{\tilde{Y}}$$$ contains all measured SMS signals in 3D Fourier encoding space including additional self-calibrating signals. This is solved using variable splitting methods under the framework of the alternating direction approach. Fig.1 shows a pictorial description of the proposed measured signal decomposition, extended controlled aliasing, extended self-calibration, and reconstruction with an SMS factor of 3 and in-plane acceleration factor of 2.

Experimental Evaluation: A set of diffusion-weighted brain data was acquired in a volunteer on a 3T whole-body MR scanner (Prisma, Siemens Healthineers, Erlangen, Germany) using a single-band multi-shot EPI through 32 receiver coils with 6 different diffusion directions (b=1000) for retrospective SMS simulation studies. Non-diffusion-weighted data was acquired using the same sequence. The imaging parameters were: TE = 64ms, field-of-view (FOV) = 230×200 mm², matrix size = 220×192, readout bandwidth = 1140 Hz/Pixel, echo train length (ETL) = 32, and Flip Angle =90^◦. Phase correction is performed for each slice before SMS simulation.

Results

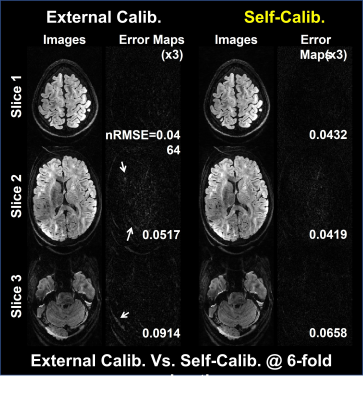
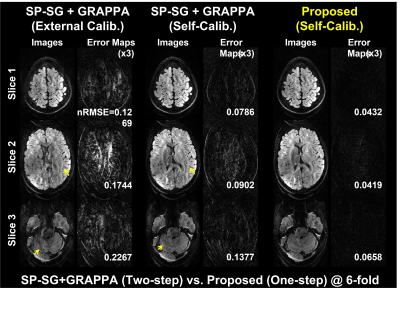
Fig.2 illustrates the dependence on the calibration data image contrast. Images with external calibration (b=0) are contaminated by aliasing artifacts, while those with self-calibrating are relatively clean. Fig.3 compares the proposed method with the SP-SG⁵ followed by GRAPPA by representing reconstructed images and the corresponding error maps using the simulated data with self-calibration. The proposed method exhibits robust suppression of artifacts and noise while the SP-SG still suffers from remaining artifacts.

Discussion and Conclusion

We successfully demonstrated the robustness of the proposed one-step k-space-based reconstruction for SMS dMRI in the presence of in-plane undersampling compared to two-step split-slice GRAPPA. It is expected that the proposed SMS method would be further improved by utilizing redundant information along diffusion direction, although it needs to be further investigated.

Acknowledgements

This work is supported in part by NRF-2018M3C7A1056887, KMDF-202011B35, and KMDF-202011C20.