3603
CEREBELLAR SURFACE PARCELLATION BASED ON DEFORMABLE SPHERICAL TRANSFORMER1School of Electronic and Information Engineering, South China University of Technology, Guangzhou, China, 2Department of Radiology and BRIC, University of North Carolina at Chapel Hill, Chapel Hill, NC, United States
Synopsis
Keywords: Segmentation, Brain
Accurate parcellation of the extremely folded cerebellar cortex is of immense importance for both brain structural and functional studies. Manual parcellation is time-consuming and expertise dependent, which motivates us to propose a novel end-to-end deep learning-based method for cerebellar cortical surface parcellation. Leveraging the spherical topology of the cerebellar surface, we propose the Deformable Spherical Transformer, which combines the advantages of the Spherical Transformer to extract the long-range dependency and the deformable attention mechanism to adaptively focus on the critical regions. Its superior performance has been validated by comparing with advanced algorithms with an average Dice ratio of 86.40%.
Introduction
In neuroimaging analysis, accurate cerebellum parcellation is the foundation of many cerebellar structural and functional studies. Manual parcellation is very time-consuming and expertise dependent. Hence, in this work, we aim to propose a novel deep learning-based method to automatically parcellate the cerebellar cortical surface, which has an intrinsic spherical topology. Motivated by the recent success of attention modeling [1,2], we have extended the self-attention mechanism to the spherical cerebral cortical surface and obtained encouraging results [3]. However, considering that the cerebellar cortex is more extensively folded than the cerebral cortex, considerable distortions may occur during the spherical mapping procedure. As a result, the regular surface partition strategy cannot extract features effectively on cerebellar spherical surfaces for their substantial inter-subject variations and demonstrate inferior performance on the critical and challenging regions, such as sharp boundaries. Therefore, an attention mechanism that can flexibly adjust the shape of the receptive field is highly desired, which motivates us to combine the deformable convolution [4] with self-attention mechanism and propose our Deformable Spherical Transformer for cerebellar cortical surface parcellation. Extensive experiments on an in-house dataset validate its superior performance against state-of-the-art algorithms.Materials and Methods
In this study, we develop and validate our method based on an in-house dataset with 9 pediatric brain MRI scans. Firstly, we extracted each cerebellum and segmented it into white matter, gray matter, and CSF [5]. Then, we reconstructed the geometrically accurate and topologically correct cerebellar cortical surface with a deformable model [6] and computed the morphological features for each vertex, including the average convexity and mean curvature. Finally, an experienced expert manually parcellated each cerebellar surface into 17 regions following the SUIT parcellation strategy [7] as the ground truth parcellation. Given the intrinsic spherical topology of the cerebellar surface, we mapped it onto a sphere [8] and then resampled the spherical surfaces to have the same tessellation on the 6-th subdivision of icosahedron with 40,962 vertices as shown in Fig. 1.To effectively extract the global long-range dependency, while preserving the local within-patch detailed information, we partitioned the spherical surface into patches in pentagon and hexagon, and further leveraged the self-attention mechanism [1] to process each patch separately. For the overlapped regions among patches, we averaged the embedding of overlapping vertices obtained from different patches as illustrated in Fig. 2. To account for geometric distortions in spherical mapping and inter-subject variability of the extremely folded cerebellar surface, we further adopted the deformable attention mechanism to flexibly extend the receptive field. Specifically, we computed the offset for each vertex with its anatomical features and a fully connected layer. Of note, the offset is defined in the spherical coordinate system rather than the Cartesian coordinate system. Then, the deformed vertices were further resampled to the standard icosahedron subdivision with a bilinear interpolation to make it differentiable. We deformed the spherical surface before conducting the surface partitioning procedure to avoid the overlapping vertices being given contradictory deformable directions in different patches. This deformable self-attention mechanism only added 1.1% overhead to the computational cost, compared to the original self-attention mechanism.
To promote the feature diversity, multiple deformable self-attention layers can be computed in parallel. Thus, a multi-layer perceptron and layer normalization module were further employed to fuse the output of the parallelized module. We name the whole procedure as a Deformable Transformer layer. To build a hierarchical feature representation, we included the spherical pooling layer and spherical transposed layer in [9]. As shown in Fig. 1, we stacked multiple deformable Transformer layers and built the overall architecture in a U-Net [10] shape, which has been widely adopted in medical image segmentation. To account for the unbalanced sizes of different regions, we adopted the Focal loss [11] as our objective function.
Results
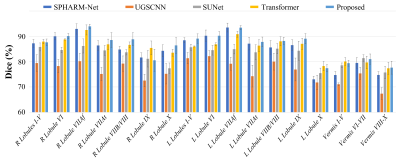
To demonstrate the generalization ability of our method, we employed the 5-fold cross-validation strategy and reported the mean and standard deviation of the Dice ratio of five test sets. As shown in Fig. 3, we compared our method with Graph Convolution-based methods [12-15], Spherical CNNs [9, 16, 17], and Spherical Transformer [3]. Our method outperforms these state-of-the-art surface parcellation methods with an average Dice ratio of 86.40%. Fig. 4 and Fig. 5 further provide a quantitative comparison of Dice ratios for each of the 17 cerebellar cortex regions and the visual comparison of the results by different methods on a random sample, respectively. It can be observed that our Deformable Spherical Transformer obtains the best result in almost all regions and demonstrates better performance on the boundaries across regions.Conclusions
In this work, we proposed a novel Deformable Spherical Transformer for automatic cerebellar surface parcellation. It differs from the previous surface Transformers by combining the deformable attention mechanisms to adaptively deform the shape and size of the receptive field, thus enabling the network to better focus on critical and challenging surface regions. We validated its superior performance against advanced algorithms with an average Dice ratio of 86.40%.Acknowledgements
G. Li is supported in part by NIH grants MH117943, MH116225, and MH123202. L. Wang is supported in part by NIH grant MH117943.
References
[1] A. Vaswani, N. Shazeer, N. Parmar, et al., “Attention is all you need,” Advances in neural information processing systems, vol. 30, 2017.
[2] A. Dosovitskiy, L. Beyer, A. Kolesnikov, et al., “An image is worth 16x16 words: Transformers for image recognition at scale,” arXiv preprint arXiv:2010.11929, 2020.
[3] J. Cheng, X. Zhang, F. Zhao, et al., “Spherical transformer for quality assessment of pediatric cortical surfaces,” in 2022 IEEE 19th International Symposium on Biomedical Imaging (ISBI). IEEE, 2022, pp. 1–5.
[4] J. Dai, H. Qi, Y. Xiong, et al., “Deformable convolutional networks,” in Proceedings of the IEEE international conference on computer vision, 2017, pp. 764–773.
[5] B. B Avants, N. Tustison, G. Song, et al., “Advanced normalization tools (ants),” Insight j, vol. 2, no. 365, pp. 1–35, 2009.
[6] G. Li, J. Nie, G. Wu, et al., “Consistent reconstruction of cortical surfaces from longitudinal brain mr images,” Neuroimage, vol. 59, no. 4, pp. 3805–3820, 2012.
[7] A. Carass, J. L Cuzzocreo, S. Han, et al., “Comparing fully automated state-of-the-art cerebellum parcellation from magnetic resonance images,” Neuroimage, vol. 183, pp. 150–172, 2018.
[8] B. Fischl, “Freesurfer,” Neuroimage, vol. 62, no. 2, pp.774–781, 2012.
[9] F. Zhao, Z. Wu, L. Wang, et al., “Spherical deformable u-net: Application to cortical surface parcellation and development prediction,” IEEE transactions on medical imaging, vol. 40, no. 4, pp. 1217–1228, 2021.
[10] O. Ronneberger, P. Fischer, and T. Brox, “U-net: Convolutional networks for biomedical image segmentation,” in International Conference on Medical image computing and computer-assisted intervention. Springer, 2015, pp. 234–241.
[11] T. Lin, P. Goyal, R. Girshick, K. He, and P. Doll ́ar, “Focal loss for dense object detection,” in Proceedings of the IEEE international conference on computer vision, 2017, pp. 2980–2988.
[12] T. N Kipf and M. Welling, “Semi-supervised classification with graph convolutional networks,” arXiv preprint arXiv:1609.02907, 2016.
[13] K. Xu, W. Hu, J. Leskovec, and S. Jegelka, “How powerful are graph neural networks?,” arXiv preprint arXiv:1810.00826, 2018.
[14] H. Gao and S. Ji, “Graph u-nets,” in international conference on machine learning. PMLR, 2019, pp. 2083–2092.
[15] W. Hamilton, Z. Ying, and J. Leskovec, “Inductive representation learning on large graphs,” Advances in neural information processing systems, vol. 30, 2017.
[16] S. Ha and I. Lyu, “Spharm-net: Spherical harmonics-based convolution for cortical parcellation,” IEEE Transactions on Medical Imaging, 2022.
[17] C. Jiang, J. Huang, K. Kashinath, et al., “Spherical cnns on unstructured grids,” arXiv preprint arXiv:1901.02039, 2019.
Figures
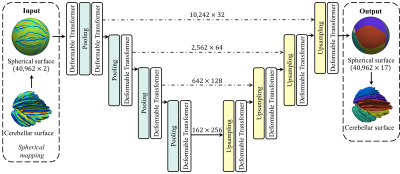
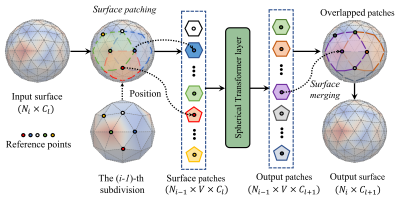
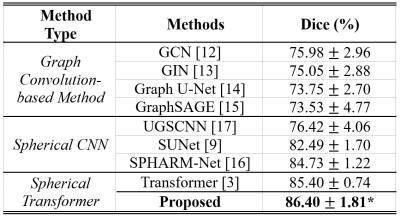
Fig. 3. Comparison of different methods for cerebellar surface parcellation in terms of Dice coefficient. * indicates statistically significant better results than other methods with p-value < 0.05 using paired t-test.