3587
Improved Brain Lesion Detection by Integrating Subspace-based Deep Learning of Normal Intensity Distributions and Bayesian Hypothesis Testing1School of Biomedical Engineering, Shanghai Jiao Tong University, Shanghai, China, 2Beckman Institute for Advanced Science and Technology, University of Illinois at Urbana-Champaign, Urbana, IL, United States, 3Department of Electrical and Computer Engineering, University of Illinois at Urbana-Champaign, Urbana, IL, United States
Synopsis
Keywords: Segmentation, Machine Learning/Artificial Intelligence, Unsupervised learning; Lesion segmentation
Unsupervised segmentation of brain lesions is desirable in many applications and has been investigated extensively. In this work, we proposed a new method for brain lesion segmentation, which effectively learns the spatial-intensity distribution of normal brain tissues and then treats lesion segmentation as an anomaly detection problem. We overcame the high-dimensional distribution learning problem using a subspace-assisted generative network. With the learned distribution, the anomaly detection problem was solved using Bayesian hypothesis testing. Our method has been validated using simulated and real brain MR images with stroke and tumor lesions, and produced significantly improved results than several state-of-the-art methods.Introduction
Automatic and accurate detection of brain lesions is essential for treatment planning of brain disorders including stroke, brain tumor, multiple sclerosis, etc. Supervised learning-based methods need large amount of high-quality lesion labels, which is usually not available. Unsupervised learning methods learn the intensity distribution of normal tissues without supervision and detect lesion voxels as an outlier or anomaly with respect to the learned distribution. A key challenge in learning the spatial-intensity distribution of normal brain tissues is high dimensionality. Previous works relied on spatial atlas1-5 or tissue-level intensity distribution modeling6, but the joint spatial-intensity features may not be well captured due to the curse of dimensionality. With the advances in deep learning, neural network-based methods have been proposed to estimate high-dimensional distribution functions using Generative Adversarial Nets (GANs)7 and Variational Auto-Encoders (VAEs)8-10. However, direct application of GANs and/or VAEs often lead to false positives or missed detection11.$$$\quad$$$This paper presents a new method for detection of brain lesions, which learn the spatial-intensity distribution of normal tissues using a subspace-based deep generative model and solve the anomaly detection problem using Bayesian hypothesis testing. The proposed method has been validated using simulated and real brain MR images with stroke and tumor lesions, producing significantly improved results as compared with state-of-the-art methods.
Methods
The proposed method learns the spatial-intensity distribution of normal brain tissues using a subspace-based deep generative model and then detects lesions as outliers using Bayesian hypothesis testing.Learning the spatial-intensity distribution of normal tissues
The spatial-intensity distribution of normal brain tissues, $$$p(\boldsymbol{x})$$$, was learned using a subspace-assisted generative network through two steps: 1) a probabilistic subspace model was applied to reduce the dimensionality and capture the global spatial-intensity dependence of normal brain tissues; 2) a subspace-assisted GAN was utilized to further capture local spatial-intensity dependence.
$$$\quad$$$More specifically, an image function $$$I\left(x_1, x_2, \ldots, x_d\right)$$$ was represented by a low-dimensional subspace model as:
$$I\left(x_1, x_2, \ldots, x_d\right) \approx \sum_{r=1}^R \alpha_r \phi_r(\boldsymbol{x})$$
where $$$\left\{\phi_r(\boldsymbol{x})\right\}$$$ is the set of basis functions obtained by applying principal component analysis to the training images $$$\left\{I_N(\boldsymbol{x})\right\}$$$, and $$$\alpha_r$$$ is the coefficient of each subspace basis. Given an image $$$\boldsymbol{y}$$$ with lesions, we obtained an initial $$$\widehat{\boldsymbol{x}}$$$ using Maximum-A-Posteriori (MAP) estimation:
$$\widehat{\boldsymbol{x}}=(1-M) \odot \boldsymbol{y}+M \odot \sum_{r=1}^R \hat{a}_r \phi_r(\boldsymbol{x}),$$
in which
$$\left\{\hat{a}_r\right\}=\arg \max _{\left\{a_r\right\}} p\left(\left\{a_r\right\} \mid \boldsymbol{y}\right)=\arg \min _{\left\{a_r\right\}}\left\|(1-M) \odot\left(\boldsymbol{y}-\sum_{r=1}^R \alpha_r \phi_r(\boldsymbol{x})\right)\right\|_2^2+\lambda \log p\left(\left\{a_r\right\}\right)$$
Here $$$M$$$ is the initial segmentation mask obtained using a Bayesian classifier.
$$$\quad$$$To further recover the higher-order spatial-intensity features in $$$\boldsymbol{x}$$$, a conditional generative adversarial model (GAN), pix2pixGAN12, was used to learn the mapping from a set of perturbation images $$$\left\{\widehat{\boldsymbol{x}}_p\right\}$$$ based on $$$\widehat{\boldsymbol{x}}$$$ to the real normal image $$$\boldsymbol{x}$$$. The adversarial learning objective was formulated as:
$$\min _G \max _{D_L} L_{a d v}=\mathbb{E}_{\boldsymbol{x} \sim p\left(\left\{I_N(\boldsymbol{x})\right\}\right)}\left[\log D_L(\boldsymbol{x})\right]+\mathbb{E}_{\widehat{\boldsymbol{x}}_p \sim p\left(\hat{\boldsymbol{x}}_p \mid \hat{\boldsymbol{x}}\right)}\left[\log \left(1-D_L\left(G\left(\widehat{\boldsymbol{x}}_p\right)\right)\right]\right.$$
With the subspace estimate $$$\widehat{\boldsymbol{x}}$$$ of $$$\boldsymbol{y}$$$, we could generate a large number of images $$$\left\{\widehat{\boldsymbol{x}}_G\right\}$$$ to approximate our target-specific posterior intensity distribution of normal tissues.
Lesion segmentation
With the learned spatial-intensity distribution of normal brain tissues, the lesion detection problem was solved using Bayesian hypothesis testing for each voxel as:
$$\text { Accept } \begin{cases}H_0 & \text { if } p\left(H_0 \mid \boldsymbol{y}\right) \geq 0.5 \\ H_1 & \text { if } p\left(H_0 \mid \boldsymbol{y}\right)<0.5\end{cases}$$
with the null hypothesis $$$H_0$$$ being normal, and the alternative hypothesis $$$H_1$$$ being abnormal. To leverage the joint spatial-intensity distribution information, we introduced a low-rank and sparse decomposition model such that:
$$\begin{aligned}&\left\{\widehat{a}_r^{\prime}\right\}=\arg \min _{\left\{a_r\right\}}\|\boldsymbol{y}-\boldsymbol{l}\|_2^2+\lambda \|\left.\boldsymbol{s}\right|_1, \\&\qquad\qquad\qquad\qquad \text { s.t. } \boldsymbol{y}=\boldsymbol{l}+\boldsymbol{s} \\&\qquad\qquad\qquad\qquad \boldsymbol{l}=\sum_{r=1}^{R^{\prime}} \alpha_r^{\prime} \phi_r^{\prime}(\boldsymbol{x})\end{aligned}$$
where $$$\phi_r^{\prime}(\boldsymbol{x})$$$ is the set of basis functions estimated from $$$\left\{\widehat{\boldsymbol{x}}_G\right\}$$$ and $$$\boldsymbol{s}$$$ is the sparse residual map with anomalies. The outputs were combined with the posterior likelihood map obtained from $$$\left\{\widehat{\boldsymbol{x}}_G\right\}$$$ for the final decision.
Results
Our proposed method is illustrated in Figure 1. We evaluated its performance using simulated data and real public ATLAS stroke (N=236) and BraTS-HGG tumor (N=131) datasets13,14. To determine the prior distribution of normal brain tissues, we used 2819 T1w brain images of healthy subjects from HCP (N = 1000)15, ADNI (N = 1269)16, and CamCAN (N = 550)17. The performance of the proposed method was compared with the state-of-the-art deep generative models7,8,10,18. Figure 2 shows that our method significantly outperformed the state-of-art methods in separating the normal tissues from the lesions in different sizes and locations. Figures 3 and 4 show that our proposed method achieved the best lesion segmentation performance in real stroke and brain tumor datasets, which is also reflected by the Dice coefficients shown in Table 1.Conclusions
This paper presents a novel method for lesion detection, which utilizes a subspace-assisted generative network to learn the spatial-intensity distribution of brain normal tissues and performs anomaly detection using Bayesian hypothesis testing. The proposed method showed significantly improved performance over the state-of-the-art methods.Acknowledgements
This work was supported by Shanghai Pilot Program for Basic Research—Shanghai Jiao Tong University (21TQ1400203); the National Natural Science Foundation of China (81871083, 62001293); and Key Program of Multidisciplinary Cross Research Foundation of Shanghai Jiao Tong University (YG2021ZD28).References
1. Van Leemput K, Maes F, Vandermeulen D, Colchester A, Suetens P. Automated segmentation of multiple sclerosis lesions by model outlier detection. IEEE Trans Med Imaging. 2001;20(8):677-688. doi:10.1109/42.9382372. Moon N, Bullitt E, Leemput K van, Gerig G. Automatic brain and tumor segmentation. In: International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer; 2002:372-379.
3. Prastawa M, Bullitt E, Ho S, Gerig G. A brain tumor segmentation framework based on outlier detection. Med Image Anal. 2004;8(3):275-283.
4. Seghier ML, Ramlackhansingh A, Crinion J, Leff AP, Price CJ. Lesion identification using unified segmentation-normalisation models and fuzzy clustering. Neuroimage. 2008;41(4):1253-1266.
5. Menze BH, Leemput K van, Lashkari D, Weber MA, Ayache N, Golland P. A generative model for brain tumor segmentation in multi-modal images. In: International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer; 2010:151-159.
6. Tomas-Fernandez X, Warfield SK. A model of population and subject (MOPS) intensities with application to multiple sclerosis lesion segmentation. IEEE Trans Med Imaging. 2015;34(6):1349-1361.
7. Schlegl T, Seeböck P, Waldstein SM, Langs G, Schmidt-Erfurth U. f-AnoGAN: Fast unsupervised anomaly detection with generative adversarial networks. Med Image Anal. 2019;54:30-44.
8. You S, Tezcan KC, Chen X, Konukoglu E. Unsupervised lesion detection via image restoration with a normative prior. In: International Conference on Medical Imaging with Deep Learning. PMLR; 2019:540-556.
9. Chen X, You S, Tezcan KC, Konukoglu E. Unsupervised lesion detection via image restoration with a normative prior. Med Image Anal. 2020;64:101713.
10. Silva-Rodríguez J, Naranjo V, Dolz J. Constrained unsupervised anomaly segmentation. arXiv preprint arXiv:220301671. Published online 2022.
11. Baur C, Denner S, Wiestler B, Navab N, Albarqouni S. Autoencoders for unsupervised anomaly segmentation in brain MR images: a comparative study. Med Image Anal. 2021;69:101952.
12. Isola P, Zhu JY, Zhou T, Efros AA. Image-to-image translation with conditional adversarial networks. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. ; 2017:1125-1134.
13. Liew SL, Anglin JM, Banks NW, et al. A large, open source dataset of stroke anatomical brain images and manual lesion segmentations. Sci Data. 2018;5(1):1-11.
14. Menze BH, Jakab A, Bauer S, et al. The multimodal brain tumor image segmentation benchmark (BRATS). IEEE Trans Med Imaging. 2014;34(10):1993-2024.
15. Glasser MF, Sotiropoulos SN, Wilson JA, et al. The minimal preprocessing pipelines for the Human Connectome Project. Neuroimage. 2013;80:105-124.
16. Jack Jr CR, Bernstein MA, Fox NC, et al. The Alzheimer’s disease neuroimaging initiative (ADNI): MRI methods. Journal of Magnetic Resonance Imaging: An Official Journal of the International Society for Magnetic Resonance in Medicine. 2008;27(4):685-691.
17. Taylor JR, Williams N, Cusack R, et al. The Cambridge Centre for Ageing and Neuroscience (Cam-CAN) data repository: Structural and functional MRI, MEG, and cognitive data from a cross-sectional adult lifespan sample. Neuroimage. 2017;144:262-269.
18. Zimmerer D, Kohl SAA, Petersen J, Isensee F, Maier-Hein KH. Context-encoding variational autoencoder for unsupervised anomaly detection. arXiv preprint arXiv:181205941. Published online 2018.
Figures
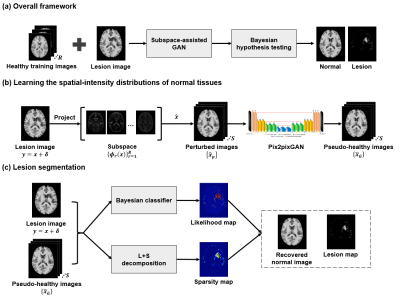
Figure 1. Illustration of the purposed brain lesion segmentation framework
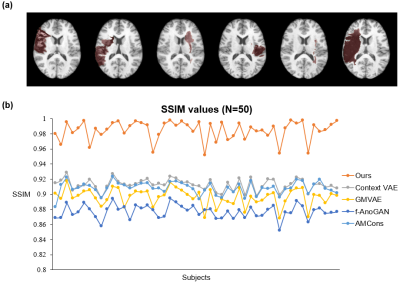
Figure 2. Comparison of normal image recovery performance on HCP test dataset with simulated stroke lesions. Top: Examples of simulated lesion images. Bottom: The structural similarity index (SSIM) between the recovered normal images and the ground truth images of all test subjects.
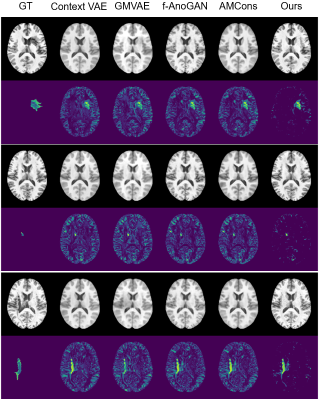
Figure 3. Recovered normal images and lesion maps in ATLAS stroke dataset. GT: ground truth.
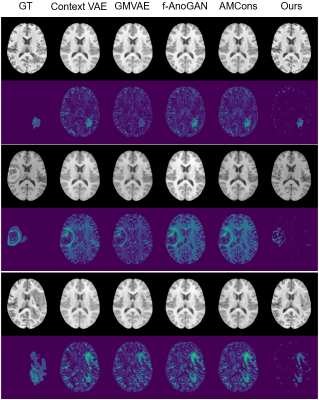
Figure 4. Recovered normal images and lesion maps in BraTS-HGG tumor dataset. GT: ground truth.
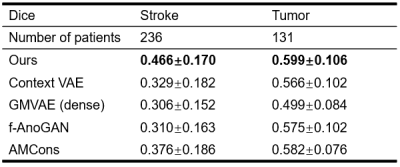
Table 1. Comparison of Dice coefficients of the proposed method with the state-of-the-art methods. Stroke: ATLAS dataset; Tumor: BraTS-HGG dataset.