3581
Joint Inversion of Multi-Echo Gradient-Echo and Spin-Echo Data for the Estimation of Myelin Water Fraction
Ségolène Dega1, Ravi Dadsena2, Hendrik Paasche1, and Tony Stöcker2,3
1Helmholtz Centre for Environmental Research (UFZ), Leipzig, Germany, 2German Center for Neurodegenerative Diseases (DZNE), Bonn, Germany, 3Department of Physics and Astronomy, University of Bonn, Bonn, Germany
1Helmholtz Centre for Environmental Research (UFZ), Leipzig, Germany, 2German Center for Neurodegenerative Diseases (DZNE), Bonn, Germany, 3Department of Physics and Astronomy, University of Bonn, Bonn, Germany
Synopsis
Keywords: Quantitative Imaging, Multi-Contrast, Myelin
Myelin water fraction (MWF) mapping using MRI has enabled researchers to directly examine myelination and demyelination in both developing and diseased brains. T2-, and T2*-weighted multi-echo data have been proposed to estimate MWF in the human brain. Even for the simple two pool signal models of myelin and non-myelin associated water, number of dimensions of the parameter space for obtaining MWF estimates remains high, making parameter estimation challenging. The aim of this research is to improve the accuracy of brain myelin mapping using a novel joint inversion imaging method that combines data from multiple contrasts in a single optimization process.Introduction
Brain myelin content is a significant imaging diagnostic biomarker that can be measured with MRI by estimating the amount of myelin water (MW), i.e., the amount of water trapped in the myelin sheath. MW has shorter relaxation times than the surrounding free water (FW). The myelin water fraction (MWF = amount of MW divided by the total amount of water) is derived from the peak areas of relaxation spectra, assuming an upper threshold for the MW component. Commonly multi-exponential relaxometry methods are employed, using either multi-echo spin-echo (ME-SE) or multi-echo gradient-echo (ME-GE) experiments1,2. The underlying inversion problem is ill-conditioned; it is susceptible to noise and measurement inadequacies, potentially leading to less accurate and more biased estimated parameters3. There are numerous methods available for extracting multi-exponential parameters from a time series. Non-negative least squares (NNLS) with regularization is the most commonly used method for MWF estimation4,5. Here we introduce a Levenberg-Marquardt (LM) inversion algorithm to jointly recover T2- and T2*-distribution, which provides MWF maps with fast computational speed and stable solutions. The method is inspired from geophysical joint inversion, where several ill-posed inverse problems are frequently jointly solved to provide stabilized and more accurate results6,7. In this research, we use the multi-exponential signal model and extended phase graph (EPG) formalism8 to generate synthetic ME-GE and ME-SE signal decay curves, respectively, with realistic myelin water composition. MWF analysis was performed with NNLS and the new LM approach, and results were compared with the ground truth. We address the effects of noise on the computation in scenarios with low to high MWF.Materials and Methods
To simulate decay curves with continuous distribution comparable to white matter, two Gaussian distributed relaxation compartments were used as shown in Figure 1 (Input Model). For myelin imaging, the distribution are thought to have two peaks, a smaller peak for MW and a larger peak representing FW. Using the EPG formalism and a simple exponential signal decay model, synthetic ME-SE and ME-GE signals were derived from the T2 & T2* distribution, respectively (cf. Figure 1, Synthetic Signals). We normalize (set integral to one) the distributions so that the integral of the fast component is directly the MWF. We can then parametrize the distributions with 9 parameters: means and standard deviations of both peaks for both distributions, and the integral of the fast component (same value for both distributions). We propose a method to estimate these parameters by forming a non-linear minimization problem (Figure 1, Inversion) with an objective function based on the difference between the "observed" (synthetic) and predicted decay curves. We iteratively solve the non-linear problem with a local-search optimization method, the Levenberg-Marquardt algorithm. At each iteration, we first perform the computation of both decay curves as described before, and then compute the Fréchet derivatives. We solve the linearized problem as a classical linear least-squares problem with bounds on the variables. We added a damping term to the cost function for more stability. In order to simulate complete imaging data, we synthesized ME-GE and ME-SE data for a given MWF distribution in the brain, which was taken from a published MWF atlas9. We add Rician distributed noise to the simulated data and perform voxel-vise MWF analysis with common NNLS and the newly proposed LM approach for individual inversion of ME-SE and ME-GE data, respectively. Finally, the LM joint inversion is performed on the combined data. The inversion is performed independently on each voxel and outputs the perturbations of the model parameters to be added to the initial model. From the final parameters obtained after the inversion, the last one gives us directly the MWF. We compute the deviation to the input MWF (ground truth) and its Root-Mean-Square-Error (RMSE) across all voxels, which serves as a metric for the accuracy of the inversion. An Apple MacBook with M1 Pro Silicon chip, 32GB RAM, and with Python 3.8 installed is used for implementing the whole pipeline. For the inversion of the MWF map, the LM approach (less than 120 seconds) was computationally less expensive as compared to NNLS (around 300 seconds).Results
Figure 2 presents the results of the estimated MWF maps using NNLS and LM for individual inversion of GE and SE data, both for SNR values of 20 and 50. As expected, RMSE decreases when SNR increases. The LM based method generally shows better performance (i.e lower RMSE) than NNLS. The MWF maps obtained through joint inversion (Figure 3) further reduce the RMSE as compared to individual inversion with LM. When using GE data with SNR=20 and SE data with SNR=50 (Fig. 3, bottom row) the joint inversion result is nearly as good as for the case SNR=50 in both datasets.Discussion
When compared to the commonly used regularized NNLS method, the LM approach results in reduction of absolute error for the estimation of MWF using either ME-GE or ME-SE data. The LM joint inversion of the combined data strongly reduces the error compared to the individual inversion. These results were obtained on synthetic data with realistic SNR values, which enable a direct comparison to the ground truth MWF. The next step is to test the approach on real MR data.Acknowledgements
This work received financial support from the Helmholtz Association, Initiative and Networking Fund, funding code ZT-I-PF-4-006 (Helmholtz Imaging Project "JIMM”).References
- MacKay, A., Laule, C., Vavasour, I., Bjarnason, T., Kolind, S. and Mädler, B., 2006. Insights into brain microstructure from the T2 distribution. Magnetic resonance imaging, 24(4), pp.515-525.
- Alonso‐Ortiz, E., Levesque, I.R. and Pike, G.B., 2018. Multi‐gradient‐echo myelin water fraction imaging: Comparison to the multi‐echo‐spin‐echo technique. Magnetic resonance in medicine, 79(3), pp.1439-1446.
- Nam, Y., Lee, J., Hwang, D. and Kim, D.H., 2015. Improved estimation of myelin water fraction using complex model fitting. NeuroImage, 116, pp.214-221.
- Zimmermann, M., Oros-Peusquens, A.M., Iordanishvili, E., Shin, S., Yun, S.D., Abbas, Z. and Shah, N.J., 2019. Multi-Exponential Relaxometry Using Regularized Iterative NNLS (MERLIN) With Application to Myelin Water Fraction Imaging. IEEE transactions on medical imaging, 38(11), pp.2676-2686.
- Wiggermann, V., Vavasour, I.M., Kolind, S.H., MacKay, A.L., Helms, G. and Rauscher, A., 2020. Non‐negative least squares computation for in vivo myelin mapping using simulated multi‐echo spin‐echo T2 decay data. NMR in Biomedicine, 33(12), pp.4277.
- Ge, X., Wang, H., Fan, Y., Cao, Y., Chen, H. and Huang, R., 2016. Joint inversion of T1–T2 spectrum combining the iterative truncated singular value decomposition and the parallel particle swarm optimization algorithms. Computer Physics Communications, 198, pp.59-70. Gavin, H.P., 2019.
- The Levenberg-Marquardt algorithm for nonlinear least squares curve-fitting problems. Department of Civil and Environmental Engineering, Duke University, pp.1-19.
- Prasloski, T., Mädler, B., Xiang, Q.S., MacKay, A. and Jones, C., 2012. Applications of stimulated echo correction to multicomponent T2 analysis. Magnetic resonance in medicine, 67(6), pp.1803-1814.
- Dvorak, A.V., Swift-LaPointe, T., Vavasour, I.M., Lee, L.E., Abel, S., Russell-Schulz, B., Graf, C., Wurl, A., Liu, H., Laule, C. and Li, D.K., 2021. An atlas for human brain myelin content throughout the adult life span. Scientific reports, 11(1), pp.1-13.
Figures
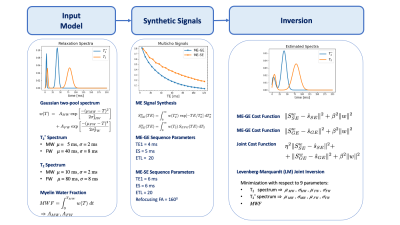
Figure 1: Workflow to test different inversion approaches. The Input Model (left column) is given by the T2 and T2* relaxation spectra, which are both defined by a Gaussian two-pool model consisting of MW and FW, where each peak has predefined mean and standard deviation. A given MWF defines the peak amplitudes. Synthetic Signals (middle column) are computed for the input model based for specific ME-GE and ME-SE sequence parameters. Inversion (last column) is carried out for cost functions of individual SE/GE data as well as for a joint approach (cf. Methods & Materials).
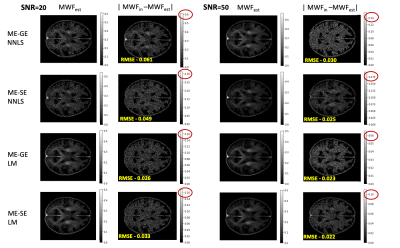
Figure 2: Estimated MWF maps for individual inversions of synthetic ME-GE and ME-SE data with NNLS and LM inversion. The two columns on the left show the estimated MWF and the deviation to the ground truth for SNR=20. The two columns on the right show the results for SNR=50. Note the difference of the maximum value in the gray-scale bars (red circles), which show the order of the maximum error.
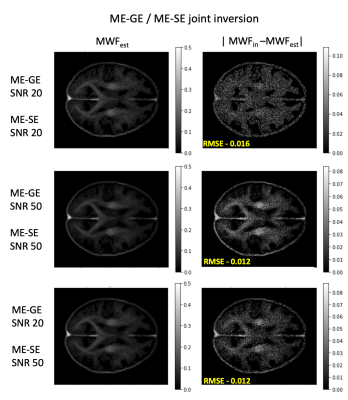
Figure 3. Estimated MWF maps (left) and difference to ground truth (right) for the joint inversion of synthetic ME-GE and ME-SE data. The 1st and 2nd row show results for SNR=20 and SNR=50 in both signals. The bottom row shows the results for SNR=20 of ME-GE and SNR=50 for ME-SE data, which corresponds to a more realistic case in real MR experiments.
DOI: https://doi.org/10.58530/2023/3581