INTRODUCTION

MR spectroscopic imaging (MRSI) can provide information about local metabolite concentrations in living tissues non-invasively ¹. However, its utility can be limited by a low signal-to-noise ratio (SNR) in practice.
Denoising methods may be utilized as a part of the preprocessing procedure to increase SNR without requiring lengthy multiple-scan acquisition ².
Denoising methods based on low-rank matrix approximation ³ have been applied for various MRS applications; However, these methods are typically computationally expensive and do not take advantage of previously acquired spectra (learning from data).
In this study, inspired by ⁴, we propose a computationally cheap data-driven approach to MRSI denoising, coined EigenMRS, by learning low-rank structures of MRS data.

METHODS

Given a set of (1D spectral) MRSI signals $$$D$$$, a Casorati matrix $$$C$$$ can be constructed. The number of rows and columns of $$$C$$$ are the number of time points and the number of signals, respectively. Matrix $$$C$$$ is an extremely low-rank matrix due to high correlations between columns ³.

Since $$$C$$$ is a low-rank matrix, a rank-$$$r$$$ (low-rank) approximations to matrix $$$C$$$ can be derived by computing singular value decomposition (SVD) of the matrix ($$$C= U \Sigma V$$$), keeping the top $$$r$$$ singular values ($$$\Sigma_r$$$) and vectors ($$$U_r$$$ and $$$V_r$$$) and discarding the rest.

Given a new measurement as a vector $$$x_{noisy}$$$, a constrained reconstruction formulation searches for the denoised vector $$$x_{denoised}$$$, which is most consistent with $$$x_{noisy}$$$ while its projection onto the subspace ($$$U_r$$$) promotes a unique solution. Mathematically, this may be expressed as:

$$ \mathop{\arg \min}\limits_{x_{denoised}} \| x_{denoised} - x_{noisy}\|_2^2 + \lambda \| U_rU_r^{\ast} x_{denoised} - x_{denoised}\|_2^2, (1)$$

where $$$\lambda$$$ and $$$\|.\|_2^2$$$ are a regularization parameter and the $$$L_2$$$ norm, respectively, and $$$\ast$$$ is the conjugate transpose. A closed-form solution for Eq. 1 can be derived as

$$ x_{denoised} = (I + \lambda(U_rU_r^{\ast} - I)^{\ast}(U_rU_r^{\ast} - I))^{-1} x_{noisy}, (2)$$

where $$$I$$$ is an identity matrix.
The simulated dataset:
The Internet Brain Segmentation Repository (IBSR) ⁵, which provides 18 manually guided expert segmentations of white matter and gray matter along with MR brain image data, was utilized to produce simulated MRSI data. The corresponding segmentation mask of each MRI volume was downsampled to the size of 64 × 64 voxels.
An MR spectrum was generated for each voxel in gray or white matter using the publicly available metabolites basis set from the ISMRM MRS study group's fitting challenge ⁶. Regional concentrations of metabolites and regional damping factors were determined randomly according to the literature^7–9. Voxel-dependent global frequency shifts induced by residual field inhomogeneity and Gaussian-distributed zeroth-order global phase shifts were added to the simulated data.
Spectra of 15 subjects were assigned to the training set to form matrix $$$C$$$, and of 3 subjects were assigned to the test set. The mean frequency-domain SNR of the training set was set to 14 ± 3 by introducing random complex Gaussian white noise.
Implementation details:
In this work, the upper limit of Marchenko-Pastur (MP) distribution ¹⁰ and the optimal singular value hard thresholding (SVHT) ¹¹ methods were utilized for automatically estimating the rank threshold from matrix $$$C$$$. In addition, the rank threshold was manually set to rank 20. The regularization parameter $$$\lambda$$$ was set to 1, 10, or 100.
By adding random complex Gaussian white noise at three noise levels with SDs of 20 (mean SNR = 24 ± 6), 35 (mean SNR = 14 ± 4), and 50 (mean SNR = 10 ± 3), 3 instantiations of the test sets were generated. The test sets were denoised For each noise level using EigenMRS and LORA³.
We have released the EigenMRS as a freely accessible pip-installable Python tool (https://pypi.org/project/eigenlearn/).

RESULTS & DISCUSSION

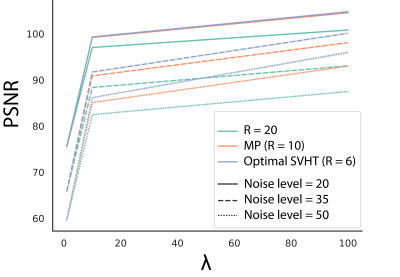
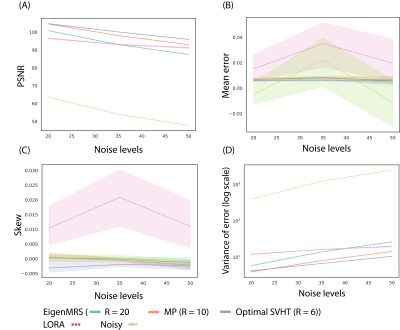
Figure 1 shows the peak signal-to-noise ratio (PSNR) ¹² of the 3 different threshold approaches at different $$$\lambda$$$. The proposed method with the highest $$$\lambda$$$(= 100) produced the highest PSNR.
Figure 2A shows the PSNR at all noise levels for the test set. EigenMRS with optimal SVHT algorithm and $$$\lambda$$$ = 100 achieved higher PSNR than LORA across all noise levels.
Figure 3B-D shows the mean error, skewness, and variance of the resulting distribution. EigenMRS with the optimal SVHT algorithm had the lowest mean (bias) at all noise levels (Figure 3B). LORA achieved higher skew than EigenMRS across all noise levels (Figure 3C).
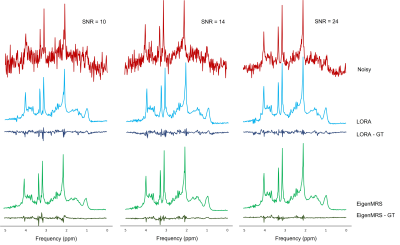
Figure 3 shows an example noisy spectrum of the test set at 3 noise levels along with denoised spectra using EigenMRS (with MP thresholding) and LORA. Both methods showed observable residuals (denoised – ground truth).
The learning time for the EigenMRS method was 54 seconds. Processing time for EigenMRS and LORA methods for one test subject were 0.1 and 2251 seconds, respectively.

CONCLUSION

We propose a computationally cheap data-driven denoising method based on low-rank structure learning. Even though the findings demonstrate that our proposed method outperforms the LORA method, we acknowledge the need for further investigation using in-vivo datasets and comparison with other approaches.

References

1. Roig ES, Feyter HM De, Nixon T, et al. Deuterium Metabolic Imaging of the Human Brain in vivo at 7T. :5-7.
2. Clarke WT, Chiew M. Uncertainty in denoising of MRSI using low-rank methods. Magn Reson Med. 2021;(July):1-15. doi:10.1002/mrm.29018
3. Nguyen HM, Peng X, Do MN, Liang ZP. Denoising MR spectroscopic imaging data with low-rank approximations. IEEE Trans Biomed Eng. 2013;60(1):78-89. doi:10.1109/TBME.2012.2223466
4. (ISMRM 2022) EigenMRI: Data-driven shallow-learning reconstruction of undersampled MRI data. https://archive.ismrm.org/2022/0501.html. Accessed October 21, 2022.
5. NITRC: IBSR: Tool/Resource Info. https://www.nitrc.org/projects/ibsr. Accessed November 9, 2022.
6. Marjańska M, Deelchand DK, Kreis R, et al. Results and interpretation of a fitting challenge for MR spectroscopy set up by the MRS study group of ISMRM. Magn Reson Med. 2022;87(1):11-32. doi:10.1002/mrm.28942
7. Robin A. de Graaf. In Vivo NMR Spectroscopy. Vivo NMR Spectrosc. February 2019:560. doi:10.1002/9781119382461.ch1
8. Wang Y, Li SJ. Differentiation of metabolic concentrations between gray matter and white matter of human brain by in vivo 1H magnetic resonance spectroscopy. Magn Reson Med. 1998;39(1):28-33. doi:10.1002/mrm.1910390107
9. Pouwels PJW, Frahm J. Regional metabolite concentrations in human brain as determined by quantitative localized proton MRS. Magn Reson Med. 1998;39(1):53-60. doi:10.1002/mrm.1910390110
10. Veraart J, Novikov DS, Christiaens D, Ades-aron B, Sijbers J, Fieremans E. Denoising of diffusion MRI using random matrix theory. Neuroimage. 2016;142:394-406. doi:10.1016/J.NEUROIMAGE.2016.08.016
11. Gavish M, Donoho DL. The Optimal Hard Threshold for Singular Values is 4/sqrt(3). IEEE Trans Inf Theory. 2013;60(8):5040-5053. doi:10.1109/TIT.2014.2323359
12. Ndajah P, Kikuchi H, Yukawa M, Watanabe H, Muramatsu S. SSIM Image Quality Metric for Denoised Images. In: Proceedings of the 3rd WSEAS International Conference on Visualization, Imaging and Simulation. VIS ’10. Stevens Point, Wisconsin, USA: World Scientific and Engineering Academy and Society (WSEAS); 2010:53–57.