Synopsis

Keywords: Signal Modeling, Brain, Relaxometry

The dual flip angle (DFA) method is widely used for brain T1 quantification. In addition to the well-known RF field effect, this study investigated the overlooked magnetization transfer (MT) effect for the accuracy of in-vivo T1 mapping. Based on the two-pool Bloch simulation, the DFA derived T1 estimation revealed FA and TR dependence, which was confirmed by the in-vivo brain T1 mapping using the same set of sequence parameters. Longer TR (30 ms) reduced the variation between FA pairs and were closer to the literature values, but at the cost of longer acquisition time.

Introduction

The dual flip angle (DFA) method¹ based on steady-state spoiled gradient echo sequences is widely used for brain T₁ quantification. DFA derived in-vivo T₁ values were shown to be in agreement with the result from the inversion recovery gold standard method in simple liquid phantom, but over 30% higher in white matter², which was attributed largely to the inhomogeneous RF field effect. The magnetization transfer (MT) effect has previously been accounted for the inversion recovery method^3-5. This study investigated the overlooked MT effect in the DFA method for the accuracy of in-vivo T₁ mapping.

Methods

To investigate the MT effect between the free water protons (WP) and the macromolecular protons (MP) on the DFA T₁ mapping method, we first established a two-pool cross-relaxation simulation model characterized by the Bloch-McConnell equation^3,6,7:
\begin{equation}\frac{dM_{z,m}}{dt} = (M_{0,m} - M_{z,m})R_m - k_m M_{z,m} + k_w M_{z,w}\\
\frac{dM_{z,w}}{dt} = (M_{0,w} - M_{z,w})R_w - k_w M_{z,w} + k_m M_{z,m}\end{equation}
Where $$$M_z$$$ is the longitudinal magnetization and $$$M_0$$$ is the equilibrium magnetization. $$$R$$$ is the relaxation rate $$$(R=1/T_1)$$$, $$$k_m$$$ denotes the magnetization exchange rate from the MP pool to the WP pool as a fraction of the MP pool, and $$$k_w$$$ denote the rate for the reverse exchange as a fraction of the WP pool.

Next, the steady-state SPGR signal $$$S_m,S_w$$$ were generated based on the two-pool model. Then, we applied the approximate DFA parameter method on our water proton signal⁸, where $$$S_{w,1}, S_{w,2}$$$ denote the water signal from two flip angles (FA) $$$\alpha_1,\alpha_2$$$, respectively, TR is the repetition time.
$$T_{1app} = 2TR \frac{ \frac{S_{w,1}}{\alpha_1} - \frac{S_{w,2}}{\alpha_2} }{ S_{w,2}\cdot\alpha_2 - S_{w,1}\cdot\alpha_1 }$$$$M_{0app} = \frac{S_{w,1}S_{w,2}\left( \frac{\alpha_2}{\alpha_1} - \frac{\alpha_1}{\alpha_2} \right)}{ S_{w,2}\cdot\alpha_2 - S_{w,1}\cdot\alpha_1 }$$
Considering the extremely short transverse relaxation times of MP⁹ ($$$T_{2,m}$$$ < 100 μs), the T₂ effect of MP was not negligible. To estimate the real flip angle for MP, we assumed $$$T_{2,m}$$$ = 70 μs.

In our two-pool simulation, these parameters were assumed^3,4: $$$R_w$$$ = 0.4 Hz ($$$T_{1,w}$$$ = 2500 ms), $$$R_m$$$ = 5 Hz ($$$T_{1,m}$$$ = 200 ms), $$$k_m$$$ = 5 Hz. $$$f_m=k_w/(k_w+k_m)$$$ where $$$f_m$$$ is the MP pool fraction, $$$f_m = 0.3$$$ for white matter and $$$f_m = 0.15$$$ for gray matter.

As for the DFA parameters, we tested combinations of three set of FA pairs ([3°, 12°]¹, [3°, 20°]², [6°, 24°]¹⁰) and three sets of TR (10, 20, 30 ms), respectively.

We applied the same nine sets of DFA parameters for steady-state spoiled gradient echo sequence sequences on a young female’s brain. The field of view (FOV) and acquisition resolution were set to be $$$220\times 220\times 80\text{ mm}^3$$$ and $$$1.2\times 1.2\times 1.2\text{ mm}^3$$$. The RF phase increment of 150$$$^{\circ}$$$ and default gradient spoiling moment of 10-20 mT$$$\cdot$$$ms/m were used. With compressed sensing factor of 4, the scan duration for each FA was 0.57 min for TR = 10 ms, 1.15 min for TR = 20 ms, and 1.72 min for TR = 30 ms. The B₁+ map was also acquired with RF-prepared 3D FLASH acquisition¹¹.

The T₁ maps are calculated based on the rational approximation of the Ernst equation¹² with and without the B₁ field correction, respectively. At a slice above the AC-PC line, white matter and cortical gray matter ROIs were segmented using empirical thresholds.

Result

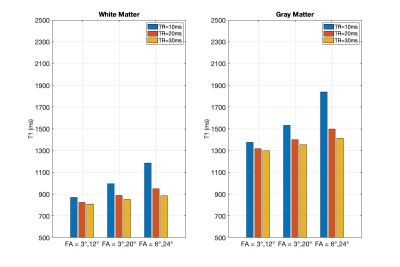
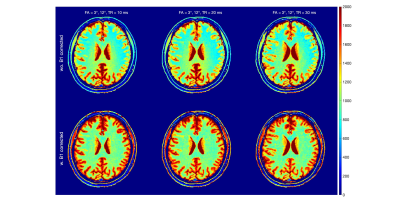
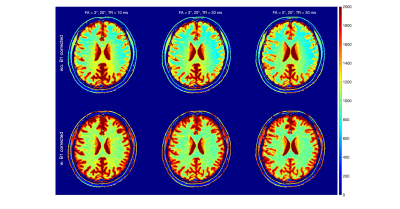
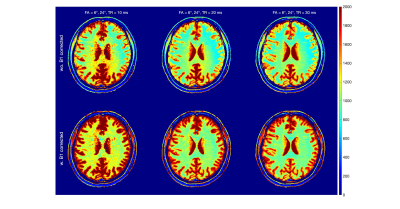
The two-pool T₁ simulation results are shown in Fig.1. For all three FA pairs and for both white matter and gray matter, the calculated T₁ values were highest at TR = 10 ms and lowest at TR = 30ms; At TR = 10ms, the T₁s were highest at FA = 6°/24° and lowest at FA = 3°/12°; The T₁s reveal much less difference between different FA pairs at TR = 30 ms than at shorter TRs.

The in-vivo T₁ Maps from the same three sets of DFA parameters are shown with the three TRs in Figs. 2-4, respectively. We compared the results without (first row) and with (second row) the B₁ correction. Compared to results before the B₁ correction, T₁ values after the B₁ correction were 68±8 ms and 278±23 ms higher in white matter and gray matter ROIs.

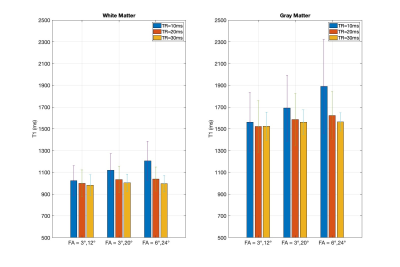
The in-vivo T₁ results after B₁ correction from white matter and gray matter ROIs are grouped with TRs for each FA pairs in Fig. 5. The result displayed a similar TR-dependent pattern as shown in the two-pool simulation result (Fig.1). At FA = 6°/24°, the averaged B₁-corrected T₁ values were 1206±179 ms and 1891±432 ms at TR = 10 ms, compared to 996±74 ms and 1564±84 ms at TR = 30 ms, for the white matter and gray matter ROIs, respectively. For the three FA pairs, the B₁-corrected T₁ values at TR = 30 ms were 982±96 ms, 1004±80 ms, 996±74 ms within the white matter ROI and 1524±129 ms, 1562±112 ms, 1564±84 ms within the gray matter ROI.

Conclusion

The consideration of MT effect resulted in the FA and TR dependence of the DFA derived T1 estimation based on the two-pool Bloch simulation, which was confirmed by the in-vivo brain T1 mapping using the same set of sequence parameters. Longer TR (30ms) reduced the variation between FA pairs and were closer to the literature white matter and gray matter values, at the cost of longer acquisition time.

Acknowledgements

No acknowledgement found.