Synopsis

Keywords: Artifacts, Artifacts, EPI, Nyquist ghost correction

This study presents a Nyquist ghost correction method by iteratively enforcing low rankness of the block-wise Hankel matrix and updating the 1D linear model for phase correction. The proposed method was evaluated with multi-shot EPI data at both ultra-high field (7T) and low field (0.3T). Compared with existing SVD-based method, the proposed method requires much fewer iterations to achieve similar performance, provides a computationally efficient and robust solution to EPI Nyquist ghost correction.

Introduction

Echo planar imaging (EPI) rapidly samples consecutive k-space lines after each RF excitation. However, it suffers from k-space inconsistencies between readouts with opposite polarities due to subtle acquisition and hardware imperfections. Such inconsistencies manifest as Nyquist ghost artifacts in the reconstructed images, directly limiting EPI quality and applications. Nyquist ghosts can be mathematically described by the slice-dependent phase difference between positive- and negative-echo images. Conventionally, it is corrected with 1D linear models using additional reference scans, navigator echoes, or EPI data itself. The linear models can be obtained from EPI data itself by minimizing image entropy[1], while it can only work for fully sampled k-space. Alternatively, the linear model can also be obtained with an SVD-based method, which iteratively minimizes the sum of N smallest singular values of the constructed block-wise Hankel matrix[2, 3]. However, its computation takes much longer time compared with entropy-based method. In this study, we propose a method that reduces the computation time by significantly accelerating the convergence.

Method

Existing SVD-based method
The existing SVD-based method seeks to minimize the sum of N smallest singular values of the constructed block-wise Hankel matrix (as a surrogate for maximizing the k-space consistency of neighboring k-space samples) by applying linear model for phase correction between data from different readout polarities. In this study, Nelder-Mead simplex method[4] is used to search for the linear model that minimizes the 20% smallest singular values. For multi-shot EPI, phase inconsistency exists both between different shots and readout polarities. To reduce the computational complexity, the SVD-based method corrects linear phase inconsistency between readout polarities and constant phase variation between shots as individual steps.
Proposed Method
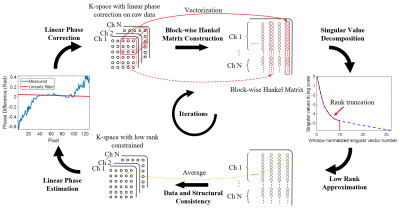
The proposed method iteratively enforces low rankness of the block-wise Hankel matrix and updates the 1D linear model for phase estimation/correction (Figure 1). Within each iteration, a block-wise Hankel matrix is constructed from the k-space, low-rank approximated with singular value decomposition (SVD) and rank truncation. The updated k-space is then recovered from the approximated low-rank matrix with data/structural consistency promoted. The whole k-space is grouped by shots and readout polarities. For each group, the phase difference between the raw k-space and the k-space with low-rank constraint is calculated and linearly fitted to model the phase error. After that, the raw k-space is phase corrected with the estimated 1D linear model. In this study, the iteration process stopped when the updated model parameters were lower than 0.001.
Evaluation with human brain imaging at 7T
2-shot GE-EPI data were collected on a 7T Siemens scanner with a 32‐channel head coil (Nova Medical, Wilmington, Delaware, USA). The acquisition parameters were TR/TE = 539/30ms, flip angle=50°, slice number=20, matrix size=128kx×128ky, echo spacing=0.7-0.8ms, bandwidth=1628Hz/pixel, and slice thickness=2mm. The kernel size was set to 3×3 for both SVD-based/proposed methods, normalized target rank was set to 1.5 for the proposed method.
Evaluation with human brain imaging at 0.3T
Human brain data were acquired on a 0.3T permanent magnet scanner (Xingaoyi Oper-0.3, Ningbo, China). The scanner was equipped with a 4-channel head coil using 2-shot SE-EPI. The acquisition parameters were TR/TE = 5500/122ms, ETL=40, matrix size=100kx×80ky, bandwidth=500Hz/pixel, FOV=240×240mm², slice thickness/gap=5/1mm. The kernel size was set to 3×3 for both SVD-based/proposed methods, normalized target rank was set to 0.7 for the proposed methods.

Results

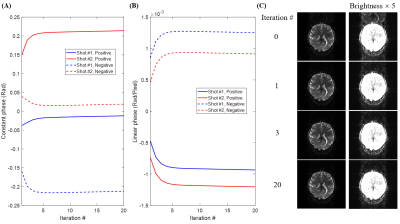
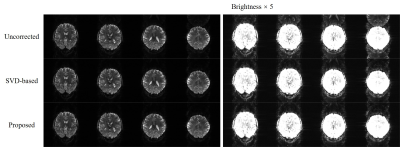
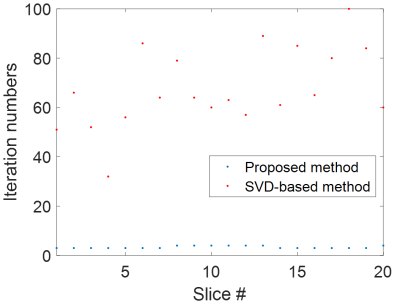
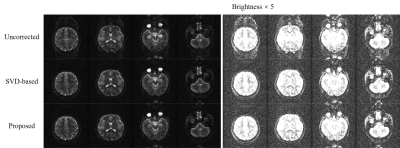
Figure 2 shows the convergency of the proposed method on a selected slice. For the data acquired at 7T, the proposed method converges within 3-4 iterations. The reconstructed image quality is visually comparable to that with 20 iterations. Figure 3 displays the EPI images at 7T with/without Nyquist ghost correction. Both SVD-based method and the proposed method successfully suppress Nyquist ghost. Figure 4 compares the iteration numbers required for SVD-based/proposed methods at 7T. To achieve comparable performance, the proposed method needs much fewer iterations. Figure 5 shows representative slices for Nyquist ghost correction at 0.3T. Though its head coil has very limited channel number and coil sensitivity spatial variation, both SVD-based method and the proposed method can effectively remove the Nyquist ghost.

Discussion

The proposed method is successfully demonstrated with multi-shot EPI in this study. It should also be applicable for single-shot non-accelerated/accelerated EPI. Note that in presence of 2D and/or nonlinear phase error, the proposed method can only remove the 1D linear components of the phase error, residual ghost induced by 2D nonlinear phase errors can be further eliminated by VC-SAKE if it significantly undermines image quality[5, 6].

Conclusions

The proposed method can robustly suppress the Nyquist ghost. Compared with existing SVD-based method, it can achieve similar performance with significantly reduced computational cost.

Acknowledgements

This study was supported by the National Natural Science Foundation of China (82202096).