Synopsis

Keywords: Artifacts, Artifacts

Intravoxel dephasing generated by Maxwell or concomitant fields can cause image artifacts like signal voids or falsify the quantification. In this study, an optimization scheme to reduce concomitant field effects in diffusion sequences with single pairs of bipolar gradients on each axis is presented. Oscillating gradients are added onto the original gradient pulses with the aim of reducing the concomitant phase without significant changes in the sequence properties. The proposed method is evaluated in both measurements and simulations, and gives rise to a positive effect on the signal for arbitrary diffusion wave vector pairs.

Introduction

Double diffusion encoding (DDE) schemes with two pairs of bipolar gradients separated by a refocusing pulse are prone to severe artifacts induced by so-called Maxwell or concomitant fields. They manifest themselves as additional non-linear phase contributions on transverse magnetization^1,2 that often corrupt measurements of diffusion metrics such as microscopic anisotropy^3,4.

In this study, we demonstrate in both simulations and measurements the positive effect of superimposing optimized oscillating gradients onto the original waveforms in the above-mentioned DDE sequences to reduce the concomitant phase without changing the sequence parameters significantly.

In particular, local gradient coils with asymmetric windings optimized to provide very high amplitudes are expected to generate significant concomitant fields, while the oscillations are easier to implement using such coils^5,6 due to higher available slew rates and higher peripheral nerve stimulation (PNS) thresholds.

Methods

Concomitant fields to the lowest order are given by $$\mathrm{B_C(x,y,z,t)}=\frac{1}{2\mathrm{B_0}}(\mathrm{G_x^2z^2+G_y^2z^2+G_z^2\frac{x^2+y^2}{4}-G_xG_zxz-G_yG_zyz}),\quad[1]$$ where the gradients $$$\mathrm{G_x}$$$, $$$\mathrm{G_y}$$$ and $$$\mathrm{G_z}$$$ alter the static magnetic field $$$\mathrm{\vec{B}_0=B_0\hat{e}_z}$$$ along the physical scanner axes $$$\mathrm{x}$$$, $$$\mathrm{y}$$$ and $$$\mathrm{z}$$$, respectively.
The concomitant phase is then given by $$\mathrm{\phi_C(x,y,z)=\gamma\int{B_C(x,y,z,t)}\,dt,\quad[2]}$$ with $$$\gamma$$$ being the gyromagnetic ratio.

The absolute remaining signal in a voxel due to the concomitant phase-induced signal loss can be numerically approximated using $$\mathrm{S_C(x,y,z)=\left|\frac{\sum_i^{N} \sum_j^{M} \sum_k^{K}e^{i \phi_C(x_i,y_j,z_k)}}{N\cdot{M}\cdot{K}}\right|},\quad[3]$$ where $$$\mathrm{N,\,M}$$$ and $$$\mathrm{K}$$$ denote the number of considered sub-voxels along each dimension, respectively.

The concomitant phase-reducing waveforms were designed using the "patternsearch" algorithm in MATLAB (The Mathworks, Inc, MA).
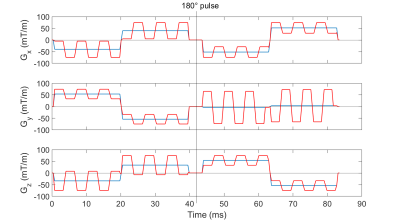
In the optimization process, for each of the 60 pairs of diffusion wave vectors published by Jespersen et al.⁴, oscillations were added onto the original gradient pulses that apply a b-value of 2000 s/mm² along every direction (Figure 1).
The sequences were optimized such that the signal loss based on Equation 3 in a transversal slice shifted by $$$\mathrm{{\Delta}z}=$$$$$$\,$$$-50$$$\,$$$mm from the isocenter with a voxel size of 3$$$\,$$$$$$\times$$$$$$\,$$$3$$$\,$$$$$$\times$$$$$$\,$$$3$$$\,$$$mm³ at $$$\mathrm{FOV=}$$$$$$\,$$$300$$$\,$$$mm$$$\times$$$300$$$\,$$$mm was minimal. $$$\mathrm{B_0}$$$ was set to 2.89 T.
These parameters were used in all further experiments in this study.

Respective constraints kept a maximum gradient amplitude of 75 mT/m, the duration of the original waveforms, and a maximum deviation of $$$\mathrm{q=\gamma\int{G}\,dt\leq}$$$$$$\,$$$50$$$\,$$$m^-1 for each modified gradient pulse as well as a total b-value deviation of 6% of the total weighting. A maximum slew rate of 188.6 mT/m/ms was allowed.

The measurements were carried out on a SIEMENS Prisma 3T imaging system using a phantom with an aqueous solution of polyvinylpyrrolidone (PVP) K30 43% (w/w) with $$$\mathrm{ADC\approx}$$$$$$\,$$$0.5$$$\,$$$μm²/ms.
100 repetitions of the optimized and original waveforms for each diffusion wave vector pair were acquired using an EPI readout ($$$\mathrm{TE}=$$$$$$\,$$$146$$$\,$$$ms, $$$\mathrm{TR}=$$$$$$\,$$$4000$$$\,$$$ms, $$$\mathrm{rBW}=$$$$$$\,$$$2000$$$\,$$$Hz/pix) with an 18-channel body coil. PNS monitoring was disabled.
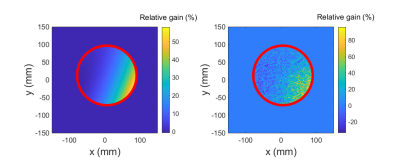
The SNR in every pixel in a ROI (Figure 2) was calculated for each sequence and corrected for the specific diffusion-induced signal loss. The relative signal gain for every diffusion wave vector pair was obtained by pixelwise division of the SNR values for the optimized and the original waveforms.

For the simulations, the remaining absolute signals for each sequence were determined using Equation 3 with $$$\mathrm{N=M=K=}$$$$$$\,$$$101 and evaluated analogously to the measurements.

Results

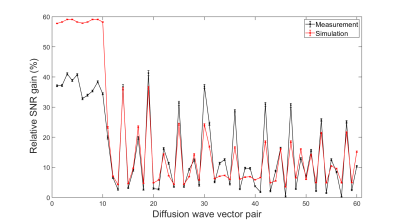
A comparison of the simulated and measured relative SNR gains in the considered ROI shows a high agreement for an example wave vector pair (Figure 2).

The calculation of the relative SNR gain for the measurements (black in Figure 3) reveals a positive measurable effect of the proposed optimization method of up to 40% for all considered pairs of diffusion directions for the parameters used, and thereby confirms the positive prediction of the simulations (red).

While the simulations predict a higher gain for the first diffusion wave vector pairs, measurements and simulations coincide relatively well for the other pairs. For these following pairs, the measurements tend to exhibit a larger gain than the simulations.

Discussion and Conclusion

As demonstrated, the addition of oscillations onto the original gradients of arbitrary pairs of encoding wave vectors enables concomitant field reduction while allowing for simultaneous diffusion weighting without changing the sequence characteristics significantly.

The proposed optimization offers additional degrees of freedom that allow for adequate shifting of the oscillation lobes to also reduce the two cross terms in Equation 1. We constrained the optimization in our study to avoid time extension of the optimized waveforms, and limited the maximum gradient amplitude to 75 mT/m, which makes the method theoretically feasible on commercially available gradient systems. The current limitation due to PNS is expected to be less relevant for local gradient coils^5,6 than for whole-body systems.

The strong oscillations applied in the optimized waveforms for the first wave vector pairs might have caused vibrations in the phantom that led to the relatively large deviations between the measurements and the simulations (Figure 2). The large number of repetitions to accurately determine the SNR led to a total acquisition time of around 14 hours, such that temperature changes might have impacted the results.

Limitations regarding the simulations include the number of sub-voxels used to determine the remaining signal. Furthermore, the actual slice profile in the measurements might be different from the assumed uniform profile in the simulations.

In summary, the proposed method leads to signal gains by reducing the concomitant phase without additional RF refocusing pulses.

Acknowledgements

No acknowledgement found.