3166
SNR-boosted whole-brain chemical exchange saturation transfer imaging by optimized variable flip angles1Key Laboratory for Biomedical Engineering of Ministry of Education, Department of Biomedical Engineering, College of Biomedical Engineering & Instrument Science, Zhejiang University, Hangzhou, Zhejiang, China, 2MR Collaboration, Siemens Healthcare Ltd., Shanghai, China
Synopsis
Keywords: CEST & MT, CEST & MT
It is well-known that the refocusing flip angles (FAs) of the SPACE sequence can be optimized to generate different image contrasts, such as T1-weighted or T2-weighted. However, the existing SPACE variable FA scheme is unsuitable for CEST imaging whose utmost aim is to increase the SNR during signal readout instead of enforcing contrast. Here, we derived a model to describe the signal-to-noise ratio (SNR) of the SPACE sequence, and maximized SNR by varying refocusing flip angles. Compared to the original constant FA protocol, the optimized variable flip angles yielded both SNR and resolution improvement.INTRODUCTION
Chemical exchange saturation transfer (CEST) relies on the attenuation of the water signal to generate contrast(1), suffering from an intrinsically low SNR. For whole-brain imaging, the SPACE-CEST sequence(2) has been endorsed by the recent amide proton transfer weighted (APTw) consensus paper owing to its high SNR efficiency and readout speed(3). However, the original SPACE-CEST work(2) used a constant refocusing flip angle (FA) of 120° without optimization. It is well-known that the refocusing FAs of SPACE can be optimized to generate different image contrasts, such as T1-weighted or T2-weighted(4,5). However, the existing SPACE variable FA scheme is unsuitable for CEST imaging whose utmost aim is to increase the SNR during signal readout instead of enforcing contrast. Here, we propose a variable FA scheme dedicated to SPACE-CEST imaging, which aims to maximize the SNR efficiency and maintain the image resolution. The optimized variable FA protocol was compared to the original constant FA protocol on healthy volunteers, demonstrating SNR improvement.THEORY
The amplitude of the i-th echo in k-space can be denoted as $${K_i} = {s_i}{w_i}$$ where $$${s_i}$$$ is the sequence-dependent amplitude arising from the FA scheme and relaxation, and $$${w_i}$$$ is the intrinsic signal attenuation coefficient due to the encoding gradient, field inhomogeneity, and other scaling factors. When using a series of 180° refocusing pulses, $$${s_i}=\exp(- i*TE/T2)$$$. While using other FAs, $$${s_i}$$$ is a function of T1, T2, and FA, and can be calculated by the Bloch equation or extended phase graph (EPG)(6). In the simplest case, when there is no encoding gradient or field inhomogeneity, $$${w_i}$$$ is 1, notwithstanding global scaling factors. Generally, $$${w_i}$$$ is smaller than 1 due to dephasing.According to Parseval’s theorem, the energy in image space is equal to that in k-space, i.e. $$\sum\limits_i{\mathop{I}\nolimits_i^2}=\sum\limits_i{\mathop{K}\nolimits_i^2}$$ where $$${I_i}$$$ denotes the voxel amplitude in image space. Assuming the noise has a constant variance, the signal in image space needs to be increased for higher SNR, which is equivalent to increasing the signal in k-space. Hence, the SNR maximization problem can be formulated as $$\eqalign{&\mathop{\max}\limits_{{\rm{FAs}}}\sum\limits_{i=1}^N{{{({s_i}{w_i})}^2}}\cr&s.t.{\rm{}}0{\le}FA\le{180^0}\cr}$$ where N is the number of refocusing echoes in each excitation shot or echo train length (ETL). Since $$${w_i}$$$ is larger at the k-space center than at the periphery, the optimization problem above would lead to an FA scheme over-focusing on the central k-space signals and consequently sacrificing spatial resolution. Thus, a resolution-related penalty term is added as $$\eqalign{&\mathop{\min}\limits_{{\rm{FAs}}}-\lambda\sum\limits_{i=1}^N{{{({s_i}{w_i})}^2}}+\mu\sum\limits_{i=1}^N{{{({s_i}-{s_{i+1}})}^2}}\cr&s.t.{\rm{}}0{\le}FA\le{180^0}\cr}$$ where $$$\lambda$$$ and $$$\mu$$$ control the tradeoff between the SNR and spatial resolution. Minimizing the resolution penalty term alone would result in constant sequence-dependent amplitudes, hence leading to an ideal point spread function (PSF).
During implementation, the intrinsic attenuation coefficient $$${w_i}$$$ is calculated as $${w_i}={{{K_i}}\over{{s_i}}}$$ where $$${K_i}$$$ is the experimentally measured k-space signal magnitude and $$${s_i}$$$ is the sequence-dependent amplitudes obtained from EPG simulations (T1=1000ms and T2=100ms). Then, the optimization problem was solved by an optimal control framework(7).
METHODS
Healthy volunteers were imaged on a 3T Siemens Prisma scanner using the SPACE-CEST sequence with constant FA(2) and optimized variable FAs. The key acquisition parameters were TR=3000ms, TE=3.4ms, ETL=140, FOV=212x212x201mm3, and acquisition matrix=76x76x72. We performed two experiments, one for SNR measurement and the other for generating APTw maps. When measuring SNR, to rule out factors that might cause spatially varying noise, the body coil was used for data acquisition, and parallel imaging was not used. The CEST reference image (S0) was acquired twice to calculate SNR. The noise was calculated as the standard deviation of the difference between the two S0 images, and the signal was calculated from their average(8). When generating APTw maps, parallel imaging was used.RESULTS
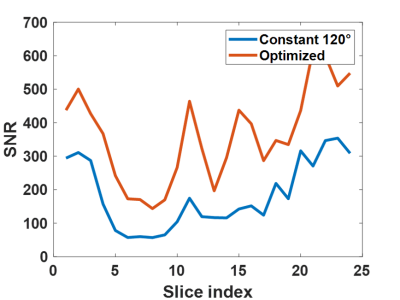
Fig. 1A shows the elliptical k-space trajectory with centric reordering, where the color marks a center-to-periphery echo order. Fig. 1B shows the portion of the k-space filled by one shot, and the other shots are rotated versions of this illustrated one. Fig. 2 illustrates the optimization results of different objective functions. When only optimizing SNR, the proposed model generated a signal curve similar to the constant 120° case (Fig. 2B), but with much smaller flip angles (Fig. 2A) and 6.1% smaller full width at half maximum (FWHM) of PSF (Fig. 2C). When only targeting spatial resolution, the proposed model yielded a constant signal curve during the majority of the echo train (Fig. 2E), leading to a PSF close to the ideal one (Fig. 2F). When optimizing both SNR and spatial resolution, the optimized flip angles yielded both 6.1% higher signal (Fig. 2H) and 12.1% smaller FWHM (Fig. 2I) than the constant 120° case. Fig. 3 shows the measured SNR across several slices in a normal volunteer, where the optimized flip angle in Fig. 2G yielded SNR consistently higher than the original constant FA case. The APTw maps revealed no visual distinction between the two FA schemes (Fig. 4).DISCUSSION and CONCLUSION
Variable flip angles have been extensively used in the SPACE sequence to optimize image contrasts. Here, we proposed a novel optimization model incorporating sequence-dependent and intrinsic attenuation factors to maximize SNR while maintaining spatial resolution for the SPACE-CEST sequence. When optimizing for both SNR and spatial resolution, the proposed model yielded improved SNR and spatial resolution, compared with the original constant flip angle strategy.Acknowledgements
National Natural Science Foundation of China: 81971605. Key R&D Program of Zhejiang Province: 2022C04031. Leading Innovation and Entrepreneurship Team of Zhejiang Province: 2020R01003. This work was supported by the MOE Frontier Science Center for Brain Science & Brain-Machine Integration, Zhejiang University.References
1. Ward KM, Aletras AH, Balaban RS. A new class of contrast agents for MRI based on proton chemical exchange dependent saturation transfer (CEST). J Magn Reson 2000;143(1):79-87.
2. Zhang Y, Yong X, Liu R, Tang J, Jiang H, Fu C, Wei R, Hsu YC, Sun Y, Luo B, Wu D. Whole‐brain chemical exchange saturation transfer imaging with optimized turbo spin echo readout. Magn Reson Med. Volume 84; 2020. p 1161-1172.
3. Zhou J, Zaiss M, Knutsson L, Sun PZ, Ahn SS, Aime S, Bachert P, Blakeley JO, Cai K, Chappell MA, Chen M, Gochberg DF, Goerke S, Heo HY, Jiang S, Jin T, Kim SG, Laterra J, Paech D, Pagel MD, Park JE, Reddy R, Sakata A, Sartoretti-Schefer S, Sherry AD, Smith SA, Stanisz GJ, Sundgren PC, Togao O, Vandsburger M, Wen Z, Wu Y, Zhang Y, Zhu W, Zu Z, van Zijl PCM. Review and consensus recommendations on clinical APT-weighted imaging approaches at 3T: Application to brain tumors. Magnetic resonance in medicine 2022;88(2):546-574.
4. Park J, Mugler JP, 3rd, Horger W, Kiefer B. Optimized T1-weighted contrast for single-slab 3D turbo spin-echo imaging with long echo trains: application to whole-brain imaging. Magn Reson Med 2007;58(5):982-992.
5. Busse RF, Hariharan H, Vu A, Brittain JH. Fast spin echo sequences with very long echo trains: design of variable refocusing flip angle schedules and generation of clinical T2 contrast. Magn Reson Med 2006;55(5):1030-1037.
6. Weigel M. Extended phase graphs: Dephasing, RF pulses, and echoes - Pure and simple. J Magn Reson Imaging. Volume 41; 2015. p 266-295.
7. Sbrizzi A, Hoogduin H, Hajnal JV, van den Berg CA, Luijten PR, Malik SJ. Optimal control design of turbo spin-echo sequences with applications to parallel-transmit systems. Magn Reson Med 2017;77(1):361-373.
8. Dietrich O, Raya JG, Reeder SB, Reiser MF, Schoenberg SO. Measurement of signal-to-noise ratios in MR images: influence of multichannel coils, parallel imaging, and reconstruction filters. J Magn Reson Imaging 2007;26(2):375-385.
Figures
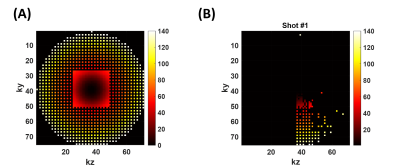
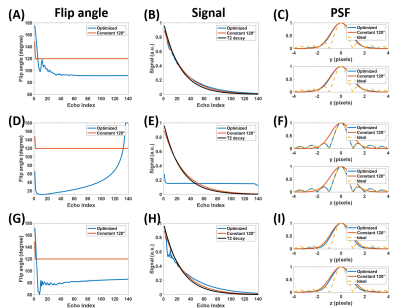
Figure 2. Optimized flip angles, corresponding signal curves along echo train (without intrinsic attenuation coefficient), and associated PSF for different objective functions. (A~C) SNR-only mode ($$$\lambda=1$$$, $$$\mu=0$$$). (D~F) Resolution-only mode ($$$\lambda=0$$$, $$$\mu=1$$$). (G~I) Combined SNR and resolution mode ($$$\lambda=1$$$, $$$\mu=0.0001$$$).