Synopsis

Keywords: Data Processing, Lung

Denoising methods can leverage common information from multiple image volumes for better noise reduction. However, performance can degrade with inter-volume misalignment or contrast changes. We proposed a block-matching denoising method for effective noise removal and robustness to inter-volume differences.

Introduction

Magnetic resonance imaging (MRI) suffers a trade-off between resolution, acquisition time, and noise level. Signal-to-noise enhancement is contributive to achieving higher resolution within clinically feasible scan times. State-of-the-art MR denoising methods utilize data redundancy for low-rank signal recovery [1,2]. Briefly, these methods combine a local data block across all volumes and channels to denoise them together, assuming blocks from different volumes share similar information, which does not hold if:

• motion cause spatial misalignment between volumes, or
• signal changes significantly across volumes.

Here, we show optimal denoising, when coupled with block matching (BM), improves noise reduction of multi-channel complex-valued (MCC) data in spite of inter-volume misalignment and contrast changes.

Methods

We implement a two-step denoising approach. First, for each volume, local 3D blocks from all channels are combined and denoised together with optimal shrinkage of singular values [3]. By denoising each volume separately, we prevent biases from inter-volume misalignments and signal changes while allowing the correlated information from multi-channel data to improve denoising power. Then, from the initially denoised data, using each 3D block in each volume as a reference, we perform non-local block-matching to find all similar blocks from all volumes and channels. Criteria for block-matching are determined as in [4]. Matching blocks are then extracted from the noisy data and then combined and denoised using optimal shrinkage of singular values. The initially denoised data are often under-denoised and used for block matching only. The reason for two-step denoising is three-fold:

• The first denoising step is intra-volume and is not affected by inter-volume misalignment or signal changes;
• Inter-volume block matching allows a block to be matched with blocks from other volumes at different spatial locations, removing the negative effects of misalignment or signal changes;
• Multiple similar blocks contain correlated information that can be used to improve denoising outcome.

We compare our block-matching multi-channel complex-valued data denoising method (BM-OSSVD) with the popular MP-PCA approach [1] and a variant of BM-OSSVD without block-matching (OSSVD) [2].

Results

Robustness to subject movements
We simulated multi-channel complex-valued dMRI from a digital phantom [5]. The data consist of 3 non-diffusion-weighted volumes and 16 diffusion-weighted volumes with b=1000 s/mm2. Each volume is then shifted randomly in 3D space to mimic subject movements causing inter-volume misalignments. Finally, complex Gaussian noise was added with SNR of 15.
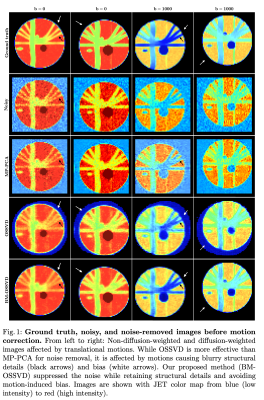
In Figure 1, MP-PCA was not effective in removing the noise due to the limited number of volumes. OSSVD was more effective than MP-PCA as it utilized the correlated information from multiple channels. However, OSSVD resulted in bias (white arrows) and blurry structures (black arrows), that are not in the ground truth, due to misalignments. Our BM-OSSVD method is robust to misalignments, providing strikingly clear results with details similar to the ground truth.
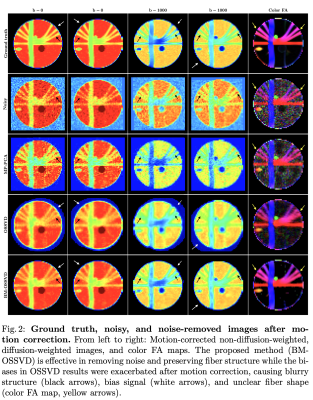
As in standard dMRI processing pipeline, we performed motion correction after denoising and computed the color-coded FA map. In Figure 2, OSSVD results were exacerbated by motion correction, producing blurs (black arrows) and bias (white arrows). BM-OSSVD yields clear detailed images similar to the ground truth.

Robustness to signal changes
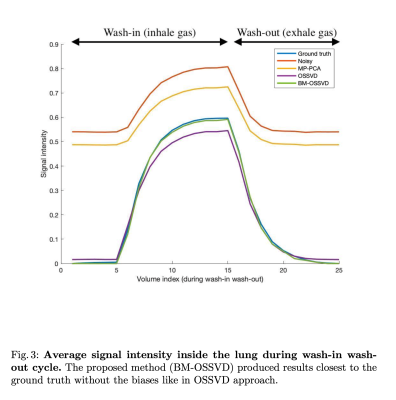
We simulated F19-contrast-enhanced lung MR images during a wash-in (inhale F19 gas, increased signal intensity) and wash-out (exhale F19 gas, decreased signal intensity) cycle. There are 25 volumes during the cycle with signal changes shown in Figure 3. Complex Gaussian noise was then added with SNR of 10.
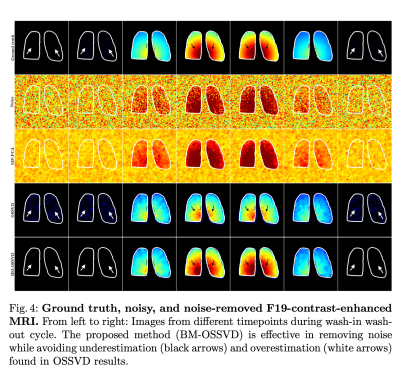
In Figure 4, OSSVD yielded more effective noise removal than MP-PCA but suffered from inter-volume signal change bias e.g. volumes with higher signal intensity have lower value after denoising and vice versa. This is because blocks from all volumes were denoised together, assuming they share similar information while they do not due to signal change. BM-OSSVD denoising only denoised similar blocks together, avoiding the overestimation (white arrows) and underestimation (black arrows) biases in OSSVD approach. Similarly, the signal curve in Figure 3 shows our method yielding the curve closest to the ground truth, preserving signal fidelity while removing noise.

Conclusion

We have presented an effective noise removal method to improve noise reduction and avoid biases caused by inter-volume misalignment and contrast variation. Our approach is not limited to diffusion MRI or F19 lung MRI but is applicable to any modality with multiple volumes (e.g. fMRI, multi TE/TR structural MRI).

Acknowledgements

This work was supported in part by the United States National Institutes of Health (NIH) through grants MH125479, EB008374, and EB006733.