Synopsis

Keywords: Image Reconstruction, Machine Learning/Artificial Intelligence

Tensor low-rank models have recently emerged as powerful alternative representations for three-dimensional dynamic MR datasets. In this paper, we introduce a novel learned transform-based tensor low-rank network for dynamic MRI based on the tensor singular value decomposition (t-SVD). Instead of manually designing the t-SVD-based transform, we propose to utilize CNN to adaptively learn the relatively optimal transformation from the dynamic MR dataset for more robust and accurate tensor low-rank representations. Experimental results on cardiac cine MRI reconstruction demonstrate the superior performance of the proposed framework compared with the state-of-the-art methods.

Introduction

Dynamic magnetic resonance imaging plays an important role in multiple clinical applications, but the artifacts from highly under-sampling pattern are inevitable. Recently, the tensor low-rank models^1-3 have been utilized to depress the artifacts and reconstruct the dynamic MR images, obtaining satisfying results. Traditional tensor low-rank models are based on CP and Tucker decomposition¹, which usually suffer from the NP-hard issues⁴, high-computational complexity¹, or the inaccuracy of the convex envelope of the tensor rank⁵.
The t-SVD decomposition⁶ avoid these issues and have been exploited in dynamic MR reconstruction⁷. Moreover, Song et al.⁸ proposed that t-SVD can be computed by the matrix SVDs of the frontal slices in a transformed domain by a one-dimensional transformation.
In this abstract, we generalize the one-dimensional transformation into an arbitrary one and adopt the convolutional neural network (CNN) to adaptively learn the relatively optimal transformation from the dynamic MR datasets.

Methods

We denote the distortion-free dynamic MR image as $$$\mathcal{X} \in \mathbb{C}^{n_{x} \times n_{y} \times n_{t}}$$$. The data acquisition of dynamic MRI can be modeled as
$$\mathbf b = A(\mathcal{X}) +\mathbf{n},$$
where $$$\mathbf b \in \mathbb{C}^{m}$$$ is the observed undersampled $k$-space data, $$$A: \mathbb{C}^{n_{x} \times n_{y} \times n_{t}} \rightarrow \mathbb{C}^m$$$ is the Fourier undersampling operator, and $$$\mathbf{n} \in \mathbb{C}^{m}$$$ is the Gaussian distributed white noise.
We propose the transformed tensor nuclear norm induced by t-SVD in arbitrary transform, namely TTNN. The dynamic MR reconstruction model of utilizing the transformed tensor low-rank prior via minimizing the TTNN can be formulated as,
$$\min_{\mathcal{X}} \frac 12 \Vert A(\mathcal{X})-\mathbf{b} \Vert_F^2+\lambda \Vert \mathcal{X}\Vert_{TTNN},$$
where $$$\lambda$$$ is the balancing parameter. The above regularized optimization can be efficiently solved by the alternating direction method of multipliers algorithm (ADMM), yielding in three substeps that are the transformed low-rank tensor prior substep, the reconstruction substep, and the multiplier update substep.
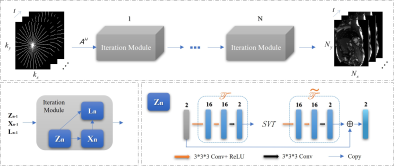
We then unfold the three substeps of the derived iterative algorithm into three corresponding blocks of the proposed LT$$$^2$$$LR-Net, i.e., the transformed low-rank tensor prior block $$$\mathbf{Z}_n$$$, the reconstruction block $$$\mathbf{X}_n$$$, and the multiplier update block $$$\mathbf{L}_n$$$. The framework of LT$$$^2$$$LR-Net is shown in Fig.1. We denote the three blocks as one iteration module corresponding to one iteration of the iterative ADMM algorithm.
We utilize two CNN within each transformed low-rank tensor prior block to adaptively learn the relatively optimal transformation and its inverse transformation from the dynamic MR image datasets. The singular value thresholding (SVT) on each frontal slice is applied between these two CNN-learned transformation in the transformed domain.

Results and discussion

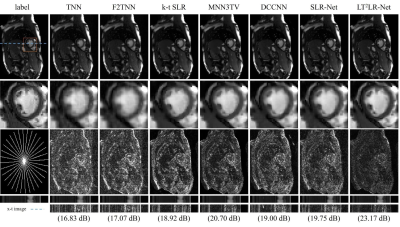
We set LT$$$^2$$$LR-Net with 15 iteration modules and evaluate it using the open-access real-time OCMR dataset⁹. We compare the proposed LT$$$^2$$$LR-Net with four iterative algorithms, namely, a tensor nuclear norm-based method: TNN¹⁰; a transformed tensor low-rank method under coupled transform of the spatial two-dimensional framelet transform and temporal FFT: F2TNN¹¹; a method combining the low-rank Casorati matrix with the total variation constraints: k-t SLR¹²; a tensor low-rank generalization of k-t SLR under Tucker decomposition incorporated with the sum of nuclear norms of unfolding matrices: MNN3TV³, and with two state-of-art unrolling networks, namely, DC-CNN¹³ and SLR-Net¹⁴.
The reconstruction results are shown in Fig.2, where the pseudo-radial under-sampling pattern¹² with 16 spokes is adopted, yielding the acceleration factor (acc) of around 10. It is observed that the reconstructed image by the proposed LT$$$^2$$$LR-Net retains the most image details and preserves the sharpest image edges compared with the other methods. In addition, the error maps show that the reconstruction performance of TLR-Net is significantly improved over the iterative methods and the unrolling networks.
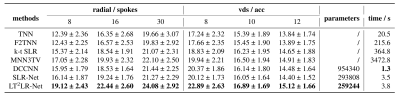
The quantitative evaluations under two sampling patterns and six different sampling cases are reported in Fig.3. It is shown that LT$$$^2$$$LR-Net can provide the highest average SNR with the least parameters and fast computation. It also indicates that LT$$$^2$$$LR-Net outstands the basic TNN and the transformed tensor low-rank method, F2TNN, which illustrates the superiority of our learned transform-based tensor low-rank network.

Conclusion

We proposed a novel deep network that learns the transform-based tensor low-rank prior in dynamic MRI. Specifically, we introduce the TTNN-based model to reconstruct the dynamic MR images, in which the ADMM is utilized to efficiently solve the problem and yield the iterative algorithm. By unrolling the three substeps of the algorithm, we proposed our LT$$$^2$$$LR-Net, which can adaptively exploit the tensor low-rank property of the dataset in a relatively optimal CNN-learned transformed domain. Reconstruction results based on the OCMR dataset demonstrated the superior reconstruction performance of our learned transform-based network compared with the state-of-the-art methods.

Acknowledgements

No acknowledgement found.

References

1. Kolda T G, Bader B W. Tensor decompositions and applications[J]. SIAM review, 2009, 51(3): 455-500.

2. He J, Liu Q, Christodoulou A G, et al. Accelerated high-dimensional MR imaging with sparse sampling using low-rank tensors[J]. IEEE transactions on medical imaging, 2016, 35(9): 2119-2129.

3. Roohi S F, Zonoobi D, Kassim A A, et al. Multi-dimensional low rank plus sparse decomposition for reconstruction of under-sampled dynamic MRI[J]. Pattern Recognition, 2017, 63: 667-679.

4. Friedland S, Lim L H. Nuclear norm of higher-order tensors[J]. Mathematics of Computation, 2018, 87(311): 1255-1281.

5. Romera-Paredes B, Pontil M. A new convex relaxation for tensor completion[J]. Advances in neural information processing systems, 2013, 26.

6. Kilmer M E, Martin C D. Factorization strategies for third-order tensors[J]. Linear Algebra and its Applications, 2011, 435(3): 641-658.

7. Zhang Y, Hu Y. Dynamic Cardiac MRI Reconstruction Using Combined Tensor Nuclear Norm and Casorati Matrix Nuclear Norm Regularizations[C]//2022 IEEE 19th International Symposium on Biomedical Imaging (ISBI). IEEE, 2022: 1-4.

8. Song G, Ng M K, Zhang X. Robust tensor completion using transformed tensor singular value decomposition[J]. Numerical Linear Algebra with Applications, 2020, 27(3): e2299.

9. Chen C, Liu Y, Schniter P, et al. OCMR (v1. 0)--Open-Access Multi-Coil k-Space Dataset for Cardiovascular Magnetic Resonance Imaging[J]. arXiv preprint arXiv:2008.03410, 2020.

10. Lu C, Feng J, Chen Y, et al. Tensor robust principal component analysis with a new tensor nuclear norm[J]. IEEE transactions on pattern analysis and machine intelligence, 2019, 42(4): 925-938.

11. Wang J L, Huang T Z, Zhao X L, et al. Multi-dimensional visual data completion via low-rank tensor representation under coupled transform[J]. IEEE Transactions on Image Processing, 2021, 30: 3581-3596.

12. Lingala S G, Hu Y, DiBella E, et al. Accelerated dynamic MRI exploiting sparsity and low-rank structure: kt SLR[J]. IEEE transactions on medical imaging, 2011, 30(5): 1042-1054.

13. Schlemper J, Caballero J, Hajnal J V, et al. A deep cascade of convolutional neural networks for MR image reconstruction[C]//International conference on information processing in medical imaging. Springer, Cham, 2017: 647-658.

14. Ke Z, Huang W, Cui Z X, et al. Learned low-rank priors in dynamic MR imaging[J]. IEEE Transactions on Medical Imaging, 2021, 40(12): 3698-3710.