3113
Parallel non-Cartesian Spatial-Temporal Dictionary Learning Neural Networks (stDLNN) for Accelerating Dynamic MRI1School of Biomedical Engineering, Shanghai Jiao Tong University, Shanghai, China
Synopsis
Keywords: Image Reconstruction, Machine Learning/Artificial Intelligence
Dynamic MRI shows promising clinical values and several applications have been investigated such as cardiac, pulmonary, and hepatic imaging. However, a successful application of dynamic MRI is hampered by its time-consuming acquisition. To improve the performance and interpretability for the accelerating reconstruction methods, we proposed the parallel non-Cartesian Spatial-Temporal Dictionary Learning Neural Networks (stDLNN), which combines the traditional spatial-temporal dictionary learning methods with the deep neural networks for accelerating dynamic MRI. It has favorable interpretability and provides better image quality than the state-of-the-art CS methods (L+S, BCS) and deep learning methods (DCCNN, PNCRNN), especially at high acceleration rate at R=25.Introduction
Dynamic MRI has shown promising clinical values1–3, and the non-Cartesian sampling trajectories are widely used because its benefits of motion correction4. However, the acquisition time is prohibitively long5,6, which makes accelerating dynamic MRI an active area of research. Dictionary learning is a kind of advanced compressed sensing (CS) methods to accelerate MRI, which introduces the adaptive dictionaries sparse coding7,8. Although dictionary learning has shown promising performance with sound interpretability, its performance is still limited at high acceleration rates and the reconstruction can be time-consuming9. With the booming of deep learning, it has demonstrated powerful ability to efficiently reconstruct MRI9–12, while the interpretability of deep learning is still an issue. To improve the interpretability and the reconstruction performance, we proposed the parallel non-Cartesian Spatial-Temporal Dictionary Learning Neural Networks (stDLNN), which combines the traditional spatial-temporal dictionary learning methods with the deep neural networks for accelerating dynamic MRI.Theory
Dictionary learning methods continuously optimize the dictionary of sparse transformation during the solving process7,13. Denote $$${\tilde{\mathbf{R}}}_i$$$ as the operator that extracts the i-th patch with the size of $$${P_s=P_x\times}{P_y\times}{P_t\times2}$$$ from the real and imaginary parts of image $$$\pmb{x}_f\in\mathbb{C}^{N_s}$$$. The structure of patches can be represented by the form $$$[P_x,P_y,P_t,2]$$$, and the total number of patches is $$$N_p$$$. $$$\tilde{\pmb{D}}\in\mathbb{R}^{P_s\times{N_d}}$$$ is the learnable dictionary with $$$N_d$$$ atoms. Then, dictionary learning can be expressed as follows:$$\min_{\pmb{x}_{f},\left\{\pmb{\gamma}_{i}\right\},\tilde{\pmb{D}}}\mu\left\|\mathbf{F}_{u}\pmb{x}_{f}-\pmb{X}_{u} \right\|_{2}^{2}+\sum_{i}^{N_{p}}(\left\|\pmb{\gamma}_{i}\right\|_{0}),\\ s.t.\left\|\tilde{\bf{R}}_{i}\pmb{x}_{f}-\tilde{\pmb{D}}\pmb{\gamma}_{i}\right\|_{2}^{2}<\varepsilon,\forall{i},$$
where $$$\mathbf{F}_\mathbf{u}$$$ denote the undersampling non-Cartesian Fourier transform, $$$\mu$$$ is the regularization parameter, $$$\pmb{\gamma}_i$$$ is the sparse representation vector. To solve the problem, the stDLNN is implemented by unrolling the iterative solving steps of the dictionary learning algorithms. The structure of the stDLNN is shown in Figure 1, which is composed of $$$M_I$$$ iterations of de-aliasing network (DN) blocks and parallel non-Cartesian data consistency (DC) blocks. The DN block plays the role of sparse coding step and image updating step in the traditional dictionary learning algorithm, where the dictionary is set as the parameter of stDLNN. The DC block achieves the multi-coil data fidelity using Toeplitz approach12,14. In the m-th DN block, patches $$${\tilde{\mathbf{R}}}_i\pmb{x}_f^{\left(m-1\right)}$$$ are extracted from the input images $$$\pmb{x}_f^{\left(m-1\right)}$$$, processed by the patch de-aliasing module (PDM), and weighted averaged into the reconstructed images $$$\pmb{z}_f^{\left(m\right)}$$$. In the PDM, the optimal sparse code $$${\hat{\pmb{\gamma}}}_i^{\left(m\right)}$$$ is calculated from the trained dictionary $$${\tilde{\pmb{D}}}_m$$$ and $$${\tilde{\mathbf{R}}}_i\pmb{x}_f^{\left(m-1\right)}$$$ using iterative soft thresholding algorithm15 (ISTA), the regularization coefficient $$$\lambda_i^{(m)}$$$ is determined by the coefficient estimation module (CEM) which is an artificial neural network containing several fully-connected layers and the de-aliased patch $$$\pmb{\psi}_i^{\left(m\right)}$$$ is reconstructed using $$${\tilde{\pmb{D}}}_m$$$ and $$${\hat{\pmb{\gamma}}}_i^{\left(m\right)}$$$.
Methods
The datasets were collected from 8 subjects (males, age 25.1±0.6) using a 3T MRI scanner (uMR790, United Imaging Healthcare, Shanghai, China). Each subject signed a consent form before the scan. The dynamic acquisition of the abdomen used the 3D golden angle stack-of-stars radial GRE sequence. The scan parameters for a 40-slice axial slab were FOV=330mm×330mm, TR=3.1ms, TE=1.49ms, flip angle=10°, and slice thickness=5mm. Each slice contained 1600 spokes with 512 sampling points in each spoke. The total scanning time was 198 seconds. The ground truth images were reconstructed by the XD-GRASP16 along with motion augmentation12. The input of algorithms was the retrospective undersampling data with the size of 256×256×30 (width-height-bin). The proposed method was compared to several state-of-the-art methods (BCS8, DLTG7, DCCNN9 and PNCRNN12) using Leave-One-Out-Cross-Validation (LOOCV).Results and Discussion
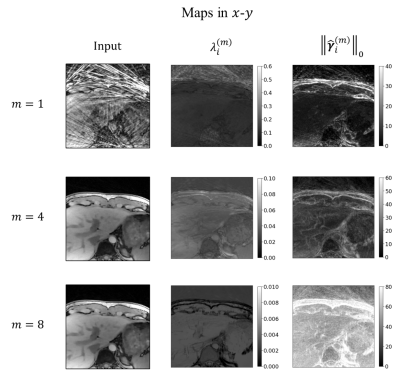
We first investigated the stDLNN with patch shape [4,4,4,2]. The reconstruction metrics across 8 subjects are summarized in Figure 2, which shows that stDLNN improves the reconstruction quality in most cases. As the acceleration rate increasing, the improvement of stDLNN is more obvious compared with other algorithms. Figure 3 presents the difference between the reconstructions and the references with the Bland-Altman plots in the ROI of all methods at R=25 in one subject. The spatial structures and the temporal profiles are improved by stDLNN, meanwhile the Bland-Altman analyses indicate that stDLNN has better control of deviation. To extend the CS methods using multidimensional full-temporal-length dictionaries, we further investigated the performance of stDLNN with patch shape [2,2,30,2] at R=25, and find that the results are very close to that with patch shape [4,4,4,2]. Its reconstruction time of 30 frames is only 0.16s, which is much less than the time of traditional dictionary learning algorithms. Figure 4 visualizes the trained dictionaries $$${\tilde{\pmb{D}}}_m$$$ in the intermediate steps ($$$m=1,4,8$$$ ) of above stDLNN. It seems to successfully learn the static and dynamic features of entire temporal dimension in the dynamic MRI data, which behaves like the multidimensional extension of the temporal bases in the BCS method. Figure 5 visualizes the maps for the regularization coefficients $$$\lambda_i^{\left(m\right)}$$$ and the $$$L_0$$$ norm of the sparse codes $$$\left\|\hat{\pmb\gamma}_{i}^{(m)}\right\|_{0}$$$, which shows the differential de-aliasing strategies learned by the network along the intermediate iterations.Conclusion
In this study, we propose a stDLNN framework to accelerate parallel non-Cartesian dynamic MRI. It combines the spatial-temporal dictionary learning with deep learning and provides improved image quality compared with the results of state-of-the-art CS methods (L+S, BCS) and deep learning methods (DCCNN, PNCRNN), especially at high acceleration rate R=25. The proposed framework has potential applications including free-breathing dynamic MRI and real-time imaging in view of its superior reconstruction quality and high computational efficiency.Acknowledgements
This research is supported in part by the National Natural Science Foundation of China under Grant 81627901 and in part by the National Key Research and Development Program under Grant 2016YFC0103905 and in part by the Natural Science Foundation of Shanghai under Grant 22TS1400300 and in partly by the Shanghai Jiao Tong University Scientific and Technological Innovation Funds under Grant YG2022QN060.References
1. Küstner T, Schwartz M, Martirosian P, et al. MR-based respiratory and cardiac motion correction for PET imaging. Medical Image Analysis. 2017;42:129-144. doi:10.1016/j.media.2017.08.002
2. Lindt TN van de, Fast MF, Wollenberg W van den, et al. Validation of a 4D-MRI guided liver stereotactic body radiation therapy strategy for implementation on the MR-linac. Phys Med Biol. 2021;66(10):105010. doi:10.1088/1361-6560/abfada
3. Ding Z, Cheng Z, She H, Liu B, Yin Y, Du YP. Dynamic pulmonary MRI using motion-state weighted motion-compensation (MostMoCo) reconstruction with ultrashort TE: A structural and functional study. Magnetic Resonance in Medicine. 2022;88(1):224-238. doi:10.1002/mrm.29204
4. Wright KL, Hamilton JI, Griswold MA, Gulani V, Seiberlich N. Non-Cartesian parallel imaging reconstruction. J Magn Reson Imaging. 2014;40(5):1022-1040. doi:10.1002/jmri.24521
5. Paulson ES, Ahunbay E, Chen X, et al. 4D-MRI driven MR-guided online adaptive radiotherapy for abdominal stereotactic body radiation therapy on a high field MR-Linac: Implementation and initial clinical experience. Clinical and Translational Radiation Oncology. 2020;23:72-79. doi:10.1016/j.ctro.2020.05.002
6. Trzasko JD, Haider CR, Borisch EA, et al. Sparse-CAPR: Highly accelerated 4D CE-MRA with parallel imaging and nonconvex compressive sensing. Magnetic Resonance in Medicine. 2011;66(4):1019-1032. doi:10.1002/mrm.22892
7. Caballero J, Price AN, Rueckert D, Hajnal JV. Dictionary Learning and Time Sparsity for Dynamic MR Data Reconstruction. IEEE Transactions on Medical Imaging. 2014;33(4):979-994. doi:10.1109/TMI.2014.2301271
8. Lingala SG, Jacob M. Blind Compressive Sensing Dynamic MRI. IEEE Transactions on Medical Imaging. 2013;32(6):1132-1145. doi:10.1109/TMI.2013.2255133
9. Schlemper J, Caballero J, Hajnal JV, Price AN, Rueckert D. A deep cascade of convolutional neural networks for dynamic MR image reconstruction. IEEE Transactions on Medical Imaging. 2018;37(2):491-503. doi:10.1109/TMI.2017.2760978
10. Wang S, Su Z, Ying L, et al. Accelerating magnetic resonance imaging via deep learning. In: 2016 IEEE 13th International Symposium on Biomedical Imaging (ISBI). ; 2016:514-517. doi:10.1109/ISBI.2016.7493320
11. Yang Y, Sun J, Li H, Xu Z. ADMM-CSNet: A deep learning approach for image compressive sensing. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2020;42(3):521-538. doi:10.1109/TPAMI.2018.2883941
12. Zhang Y, She H, Du YP. Dynamic MRI of the abdomen using parallel non-Cartesian convolutional recurrent neural networks. Magnetic Resonance in Medicine. 2021;86(2):964-973. doi:10.1002/mrm.28774
13. Ravishankar S, Bresler Y. MR Image Reconstruction From Highly Undersampled k-Space Data by Dictionary Learning. IEEE Transactions on Medical Imaging. 2011;30(5):1028-1041. doi:10.1109/TMI.2010.2090538
14. Muckley MJ, Stern R, Murrell T, Knoll F. TorchKbNufft: A High-Level, Hardware-Agnostic Non-Uniform Fast Fourier Transform. In: ISMRM Workshop on Data Sampling & Image Reconstruction. ; 2020.
15. Beck A, Teboulle M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J Imaging Sci. 2009;2(1):183-202. doi:10.1137/080716542
16. Feng L, Axel L, Chandarana H, Block KT, Sodickson DK, Otazo R. XD-GRASP: Golden-angle radial MRI with reconstruction of extra motion-state dimensions using compressed sensing. Magnetic Resonance in Medicine. 2016;75(2):775-788. doi:10.1002/mrm.25665
Figures
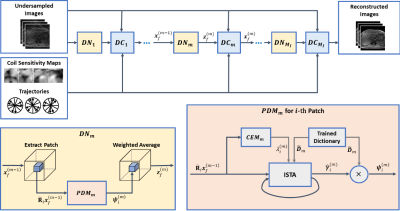

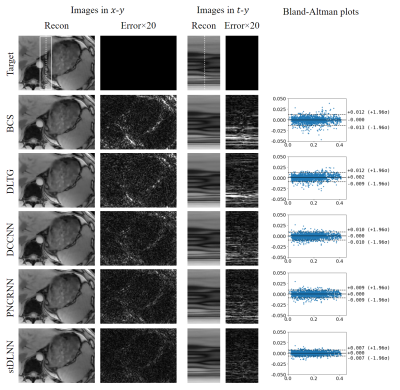
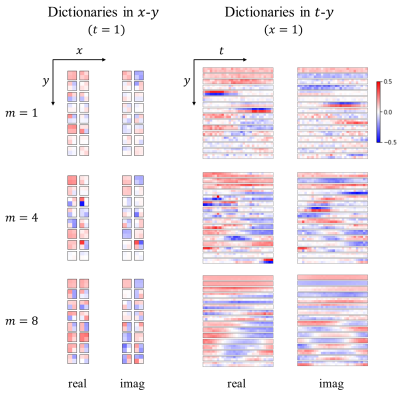
Figure 3: Visualization of the learned dictionary $$${\tilde{\pmb{D}}}_m$$$ in the intermediate steps ($$$m=1,4,8$$$) of stDLNNat R=25. The patch shape of stDLNN is [2,2,30,2], and $$$M_I=8$$$, $$$N_d=160$$$. The 4D dictionaries are displayed in spatial (x-y) and spatial-temporal (t-y) dimensions while the real and imaginary parts are shown side by side. Note that only 16 out of 160 atoms are shown for every step, and each dictionary atom is composed of both the real and imaginary parts.