Synopsis

Keywords: Image Reconstruction, Machine Learning/Artificial Intelligence

Diffusion tensor imaging (DTI) needs a large number of diffusion-weighted images (DWIs) to reliably reconstruct the diffusion measurements of the brain white matter, making the data acquisition time-consuming. Deep learning has emerged as a powerful technique to reduce the number of acquired DWIs. While most existing deep learning methods are supervised and need high-quality ground truth data as the training labels. Here, we proposed an unsupervised and subject-specific DTI reconstruction method called DTI-Net to significantly reduce the required number of DWIs, while also can simultaneously conduct the super-resolution reconstruction of the tensors.

Introduction

Diffusion Tensor Imaging (DTI)¹ is a powerful technique to map tissue microstructure using a second-order tensor model. Although the tensor model theoretically requires only six diffusion-weighted images (DWIs) and one non-diffusion encoded image for tensor reconstruction, a large number of DWIs are always required in practice because the tensor model is sensitive to noise contamination. It would significantly increase the scan time and thus increase the patients’ discomfort and is vulnerable to motion.
Deep learning has emerged as a promising technique to reduce the number of required DWIs due to its strong learning capacity. However, traditional convolutional neural network (CNN)-based reconstruction methods, such as DeepDTI² and SuperDTI³, require the corresponding high-quality ground truth data and have generalization issues when testing on the data acquired with different acquisition parameters. Implicit neural representation (INR)⁴ is a recently developed technique that parameterizes the signal as a continuous function and learns this continuous representation by regressing the spatial coordinate to the objective volume intensity using multi-layer perception (MLP). It is unsupervised and training databases free. Inspired by INR, we proposed an unsupervised and subject-specific DTI reconstruction method, DTI-Net, to simultaneously reconstruct DTI and perform super-resolution reconstruction with a significantly reduced number of DWIs.

Methods

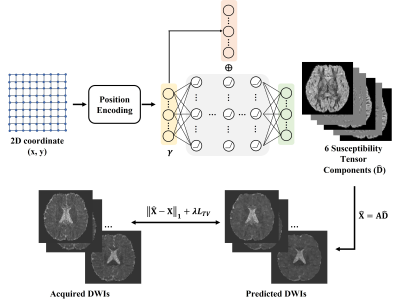
DTI-Net Pipeline
The overview structure of the proposed DTI-Net is displayed in figure 1. DTI-Net uses MLP to map the 2D coordinates $$$(x,y)$$$ to the corresponding tensor field, with MLP weights adjusted for each reconstructed sample. Before the first layer of MLP, 2D spatial coordinate was projected to a higher dimension using position encoding⁵ to better represent high-frequency signals. The MLP contains 9 fully connected (FC) layers and there is a residual connection between the first layer and the fourth layer, with each layer followed by ReLU activation except the last layer. The output layer predicted 6 tensor elements ($$$\mathbf{D} = {\left[ {{D_{xx}},{D_{xy}},{D_{xz}},{D_{yy}},{D_{yz}},{D_{zz}}} \right]^T}$$$) by 6 channels, separately. Then the predicted tensor was used to calculate as equation (1) that is derived from DTI model.
$$ \mathbf{X} = - {{ln({S_i}/{S_0})} \over b} = \mathbf{g_i}^TD\mathbf{g_i} = \mathbf{AD}\tag{1}$$
$$$\mathbf{g_i} = {[{g_{ix}},{g_{iy}},{g_{iz}}]^T}$$$ is the unit vector of diffusion-encoding direction. $$${{S_i}}$$$ is the DWI signal and $$${{S_0}}$$$ is the non-diffusion image, $$$b$$$ is the b-value. $$$\mathbf{A} = [\mathbf{a_1},\mathbf{a_2},...,\mathbf{a_n}]$$$ is the diffusion tensor transformation matrix that depends on the diffusion-encoding directions with $$$\mathbf{a_i} = [g_{ix}^2,2{g_{ix}}{g_{iy}},2{g_{ix}}{g_{iz}},g_{iy}^2,2{g_{iy}}{g_{iz}},g_{iz}^2]$$$ and $$$n$$$ is the number of DWIs. Finally, the loss function is defined as equation (2).
$$L = {\left\| {\mathbf{A\widehat D} - \mathbf{AD}} \right\|_1} + \lambda {\left\| {\nabla \mathbf{\widehat D}} \right\|_1}\tag{2}$$
$$$\lambda $$$ is the weight of total variation (TV) loss which we set as 0.5 in this study.
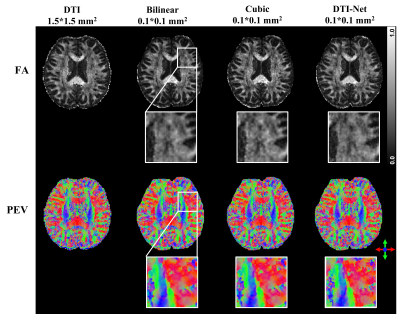
We compared the proposed DTI-Net to the conventional DTI reconstruction method using 6, 9 and 12 DWIs. In addition, we also tested the DTI-Net and traditional bilinear and cubic interpolation methods for super-resolution reconstruction with 15-fold upsampling.

Data Acquisition
DTI data were acquired using a spin-echo echo planar imaging (SE-EPI) sequence: FOV = 210×210×156 mm³, matrix size = 140×140×104, flip angle = 90°, TR = 4500 ms, TE = 72 ms, spatial resolution = 1.5×1.5×1.5 mm³. The DTI data sets were acquired with 5 b0 images and 1 b-values of 1000 s/mm² with 64 diffusion encoding directions. For experiments, we used only one slice for 2D reconstruction.

Results

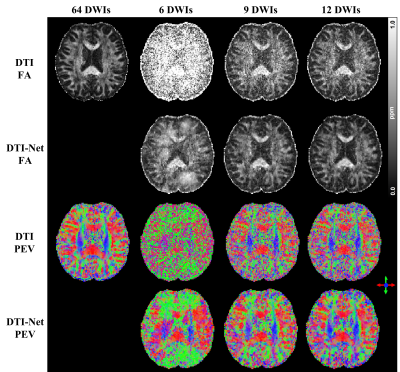
Figure 2 shows the reconstruction results using 6, 9, and 12 DWIs when using the DTI results derived from 64 DWIs for reference. DTI-Net could effectively reduce noise contamination when the number of DWI was reduced to 9 or 12. The FA and PEV results from DTI-Net using 12 DWIs are very similar to the reference results. For super-resolution reconstruction, as shown in figure 3, there exist many high-intensity points in FA images upsampled by bilinear and cubic interpolation methods, while DTI-Net’s FA shows more continuous anatomical structures. For upsampled PEV, DTI-Net shows a more reasonable color change in white matter fibers.

Discussion

In this study, we proposed a deep learning-based method for DTI reconstruction using implicit neural representation, DTI-Net, to reduce the number of DWIs for DTI reconstruction. DTI-Net is subject-specific and training databases free. The proposed DTI-Net shows the powerful capacity for reconstructing high-quality DTI results using fewer DWIs, which effectively reduces the acquisition time. Additionally, DTI-Net learns continuous representation from discrete measurements, leading to better super-resolution reconstruction results than traditional interpolation methods.

Conclusion

In conclusion, our preliminary results indicated that the proposed DTI-Net has the potential to effectively reduce the number of acquired DWIs for high-quality DTI reconstruction and is able to simultaneously upsample the DTI results to arbitrary resolution.

Acknowledgements

No acknowledgement found.