Synopsis

Keywords: Image Reconstruction, MR Fingerprinting, Tensor Low-rank, CP Decomposition, Bloch Response Manifold, non-Cartesian

We propose a deep unrolled network for non-Cartesian MRF reconstruction by unrolling the MRF reconstruction model regularized by the tensor low-rank and the Bloch resonance manifold priors. To avoid computationally burdensome singular value decomposition, we propose a learned CP decomposition module to exploit the tensor low-rank priors of MRF data. Inspired by the MRF imaging mechanism, we also propose a Bloch response manifold module to learn the mapping between reconstructed MRF data and the multiple parameter maps. Numerical experiments show that the proposed network can improve the reconstruction quality of MRF data and multi-parameter maps within significantly reduced computational time.

Introduction

MRF is a quantitative MRI framework proposed by Ma et al.^[1], which can rapidly perform simultaneous imaging of multiple tissue parameters such as spin-lattice relaxation time ($$${\rm T}_1$$$), and spin-spin relaxation time ($$${\rm T}_2$$$). MRF uses pesudo-randomized pulse sequences to acquire data, resulting in unique signal evolution from different tissues, known as tissue fingerprints. The quantization parameters are then obtained by mapping tissue fingerprints to a dictionary containing all tissue theoretical fingerprints. Rapid acquisition schemes are widely used in MRF, which accelerate data acquisition but also inevitably introduce aliasing artifacts in the recovered tissue fingerprints^[2].

To improve the accuracy of the estimated parameter maps, many reconstruction methods have been proposed to overcome undersampling artifacts. Davis et al.^[3] proposed to apply Bloch response manifold projection in a compressed sensing framework to improve MRF reconstruction. Mazor et al.^[4] developed a subspace-constrained low-rank projection method (FLOR), based on the fact that the MRF signal can be sparsely represented in the generated dictionary domain. Traditional regularized reconstruction methods are usually burdened with high computational complexity, especially in non-Cartesian scenarios. Recently, deep learning-based methods have been introduced in MRF to improve the speed and accuracy of parameter map estimation. Fang et al.^[5] proposed a two-step deep learning model (SCQ) to learn the mapping from the signals to the tissue parameters, enabling accurate parametric reconstructions under quadruple accelerated acquisition. Chen et al.^[6] reconstructed data and parameter maps from non-Cartesian samples based on the deep unrolling network. Deep unrolling-based methods^[7][8] have the interpretability of model-based iterative methods while being able to exploit the powerful learning capabilities of neural networks. However, most of the existing approaches are less interpretable due to directly reconstructing parameter maps with specific networks. In addition, most deep learning-based methods cannot directly reconstruct MRF data from non-Cartesian undersampled measurements.

Methods

Based on the assumption that the resonance $$${\cal X}_{i,j,:}$$$ of each voxel can be projected onto the Bloch response manifold $$${\cal B}$$$, we can formulate the MRF reconstruction problem as the following convex optimization problem:
$$\min_{{\cal X} \in {\cal B}} \lVert {\cal A}{\cal X}-{\mathbf{b}} \rVert_2^2+\lambda{\cal J}({\cal X})$$
where $$${\cal J}({\cal X})$$$ is the tensor low-rank regularization term. The general steps for solving above problem by the incremental proximal method are as follows:
$${\mathbf Z}_k = {\cal X}_k+\mu {\cal A}^H({\cal A}{\cal X}_k-{\mathbf{b}})$$
$$\hat{\mathbf{Z}}_k = {\cal P_B}(\mathbf{Z}_k)$$
$${\cal X}_{k+1} = \arg\min_{\cal X} \lambda{\cal J}({\cal X})+\frac{1}{2\mu}\lVert {\cal X}-\hat{\mathbf{Z}}_k \rVert_2^2$$
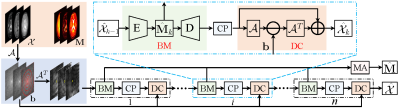
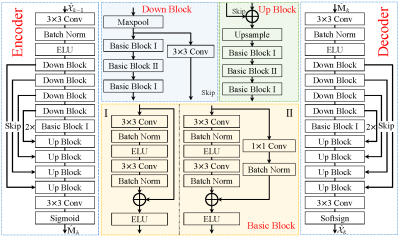
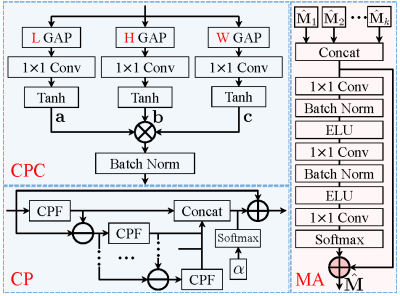
where $$${\cal P_B}(\cdot)$$$ denotes projection onto the Bloch response manifold $$${\cal B}$$$, and $$$\mu$$$ is a positive step size. The above iterative procedures take a relatively long computational time to obtain a high-quality reconstruction. Besides, the selection of the regularization parameter is time-consuming and tedious. To address these problems, we unroll the above iterations into a deep neural network, as shown in Fig.1. The three procedures correspond to the three modules in the proposed TLR-BM-Net, which are named the data consistency module (DC), the learned Bloch response manifold module (BM), and the learned CP decomposition module (CP). The proposed BM module is introduced through an encoder-decoder network to learn the mapping between reconstructed MRF data and the Bloch response manifold, as shown in Fig.2. To avoid computationally burdensome singular value decomposition, a learned CP decomposition module (as shown in Fig.3), which represents a tensor as the sum of a finite number of rank-one tensors^[9], is proposed to exploit the tensor low-rank priors of MRF data. We add a parameter map aggregation module (MA) at the end of the network to aggregate all the parameter maps ($$$\hat{\mathbf{M}}_k, k=1,\cdots,n$$$) estimated by BM modules into the final parameter map $$$\hat{\mathbf M}$$$, as shown in Fig.3.

Results and discussion

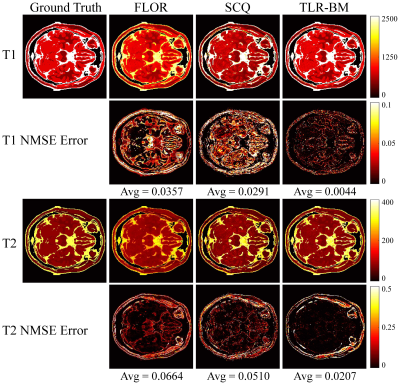
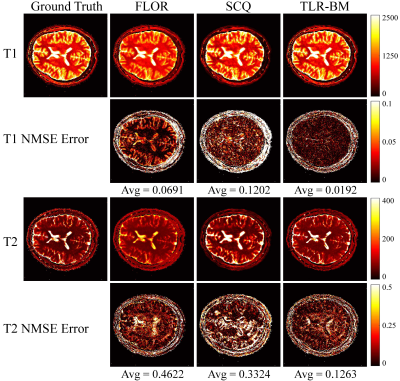
The datasets used in this study consist of two parts: simulation data and in vivo data. The simulation data was generated by using the parametric map taken from Brainweb. The in vivo data were acquired on a 3T Siemens Prisma scanner from 8 healthy volunteers across 10 slices each. All the acquired data were reconstructed using the SL-SP^[10] method to obtain the parametric map as the ground truth. We used 36 spiral trajectories (see Fig.4) to acquire 2880 samples in each frame, resulting in an undersampling ratio of ~ 6%. ~10% of the dataset is used for testing and the rest for training. We performed experiments at a sequence length of 500.

We compare the performance of the proposed TLR-BM method with FLOR (low-rank constrained)[5] and SCQ (end-to-end network)[7]. Fig.5 and Fig.6 show the parameter maps reconstructed by different methods from one set of simulated data and in vivo data in the test dataset, respectively. Table.1 shows quantitative comparison results of different methods on the test dataset. Experimental results show that our proposed method has a comparable reconstruction speed to end-to-end networks while having the best reconstruction performance among all methods.

Conclusion

In this paper, we proposed a deep unrolled network for non-Cartesian MRF reconstruction by unrolling the MRF reconstruction model regularized by the tensor low-rank and the Bloch resonance manifold priors. We proposed a learned CP decomposition module to explore the tensor low-rank priors and a learned Bloch response manifold module to project between the reconstructed MRF data and the Bloch response manifold.

Acknowledgements

This work is supported by China NSFC 61871159 and Natural Science Foundation of Heilongjiang YQ2021F005.