3106

Motion-mitigated reconstruction of accelerated MRI by using an unfolded variational network

Zijian Zhou^1,2, Haikun Qi^1,2, and Peng Hu^1,2
¹School of Biomedical Engineering, ShanghaiTech University, Shanghai, China, ²Shanghai Clinical Research and Trial Center, Shanghai, China

Synopsis

Keywords: Image Reconstruction, Motion Correction

Motion-mitigated reconstruction of highly undersampled MRI was achieved by adding a motion estimation module to the data consistency part of the model-based unfolded variation network. The motion estimation module consisted of a pair of convolutional blocks with residual inputs and added only limited number of trainable parameters to the network. The network was trained and tested on synthesized motion-corrupted images from a publicly available knee dataset. The reconstructed images with the proposed motion estimation module were sharper, and details were better recovered, with the structural similarity and peak signal-to-noise ratio significantly improved.

Introduction

Compressed sensing MRI has been broadly used for various clinical imaging tasks. The diagnostic-quality images can be reconstructed from the highly undersampled k-spaces using iterative reconstruction algorithms^1,2. However, the reconstruction typically takes tens of minutes. The long reconstruction time could limit its applications and cause delay in clinical workflows. On the other hand, although fast MR imaging is less sensitive to motion, respiratory and other involuntary motion of the patient may still degrade the image quality. Navigator- and surrogate signal-based methods achieved good results for motion compensation^3,4, however, they may be limited to rigid motion and increase scan complexity.

Recently, a model-based deep learning reconstruction method was proposed to reconstruct highly undersampled images and showed promising results^5,6. In this approach, the network is unfolded to several stages, mimicking iterations of the conventional reconstruction method. In each stage, the regularization (or denoising) term is replaced by a learnable module, and the data consistency term is updated using one or multiple steps of conjugate gradient optimization. Studies have integrated modules into the network for joint reconstruction and motion estimation (ME) between frames of cardiac cine imaging^7,8; however, most of the studies did not consider object motion during acquisition. In this study, we aim to integrate ME into the data consistency part of the network to achieve motion-mitigated reconstruction for accelerated MRI.

Theory

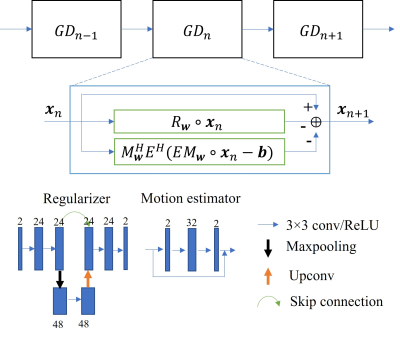
The reconstruction process can be formulated as seeking the optimal solution to an inverse problem:$$x=\arg\min_{x}||A\cdot x-b||_2^{2}+λR(x)\tag{1}$$where $$$x$$$ is the image to be reconstructed. For the data consistency term, $$$A$$$ is the encoding operator including coil sensitivity map multiplication, Fourier transform, and undersampling, and $$$b$$$ is the acquired k-space data. Variational network uses iterative optimization to solve Equation (1). Based on gradient descent, the network iteratively optimizes the image following:$$x_{n+1}=x_n-R_w(x_n)-A^H(A\cdot x_n-b)\tag{2}$$where $$$R_w$$$ is now a learnable subnetwork with parameters $$$w$$$. For each iteration, the parameters can be shared or independent.

To compensate for the object motion during acquisition, the motion operator needs to be considered in $$$A$$$. Here, we propose using two separate subnetworks for the motion ($$$M$$$) and its Hermitian operator ($$$M^H$$$), respectively. The motion-mitigated reconstruction now is:$$x_{n+1}=x_n-R_w(x_n)-M_w^HE^H(EM_w\cdot x_n-b)\tag{3}$$where the two motion operators are both learnable with their respective parameter sets $$$w$$$ and $$$E$$$ includes other encoding operators. Based on the end-to-end training and gradient descent, we hypothesize that the ME operators can also be learned from the supervised training.

Methods

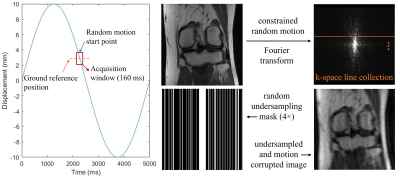
The study was performed using a publicly available dataset of the FastMRI challenge (https://fastmri.org). We currently simulated random translational motion for the 2D knee magnitude images. The random motion was constrained to be continuous in each direction during the acquisition window. The matrix size of the ground reference image was 320×320. For the simulation purpose, we assumed an acquisition window of 160 ms for each image, considering 25% undersampling using a balanced steady-state free precession sequence9 with a TR of 2 ms (Figure 1). To save computation power, we used emulated single coil data for the study.

Our model-based network had two sections. For the regularization section, we used a U-Net to learn the aliasing artifacts, which permits convolutions on feature maps of different scales. For the data consistency section, we added two different sets of networks to estimate motion ($$$M_w$$$, $$$M_w^H$$$). The ME modules were stacked convolutional layers with residual connections (Figure 2). The number of optimization stages was 10 without weight sharing, and the total number of parameters was 0.73 million. The network was optimized using L1 loss between the reconstructed and reference images. Using 500 slices of 25 patients, the network was trained 600 epochs with a learning rate of 0.001. It was then tested on the same number of slices of another 25 patients. To investigate the efficacy of the ME module, we also trained a network without such module for comparison.

Results

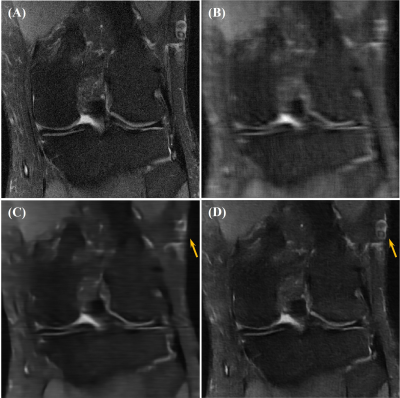
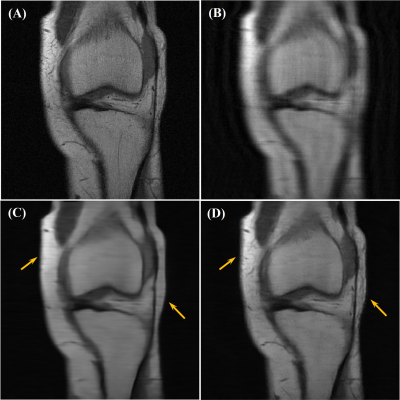
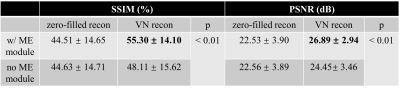
Our network achieved good results in reconstructing the undersampled and motion-corrupted images. For testing, the reconstruction time was around 0.14 s/slice. Compared to the zero-filled reconstruction, the structural similarity (SSIM) was improved by 11%, and the peak signal-to-noise ratio (PSNR) was improved by 4.4 dB. Without using the ME module, the reconstruction SSIM was improved by 3.5%, and the PSNR was improved by 1.9 dB (Figures 3, 4 and Table 1).

Discussion

By training an unfolded variational network with the ME module, we were able to reconstruct highly undersampled and motion-corrupted knee MR images. With the relatively small number of parameters, variational network permits robust training with limited number of patients and achieves fast reconstruction. Combining with other fast MRI techniques, they can potentially be used for real-time motion-mitigated imaging. However, our network is currently limited to magnitude images. Future work includes extending the motion-mitigated reconstruction to complex-valued images, which may be achieved by modifying the ME module or use a complex-valued network. We will also integrate conjugate gradient methods to the network to further improve its performance.

Conclusion

In conclusion, by adding ME modules to the unfolded variation network, motion-mitigated reconstruction of highly accelerated MRI can be achieved.

Acknowledgements

No acknowledgement found.

References

[1] Lustig M, Donoho D, & Pauly JM. Sparse MRI: the application of compressed sensing for rapid MR imaging. Magn Reson Med. 2007;58:1182-1195.

[2] Knoll F, Bredies K, Pock T, et al. Second order total generalized variation (TGV) for MRI. Magn Reson Med. 2011;65:480-491.

[3] Ehman RL & Felmlee JP. Adaptive technique for high-defination MR imaging of moving structures. Radiology. 1989;173(1):255-263.

[4] Li X, Lee YH, Mikaiel S, et al. Respiratory motion prediction using fusion-based multi-rate Kalman Filtering and real-time golden-angle radial MRI. IEEE Trans Biomed Eng. 2020;67(6):1727-1738.

[5] Hammernik K, Klatzer T, Kobler E, et al. Learning a variational network for reconstruction of accelerated MRI data. Magn Reson Med. 2018;79:3055-3071.

[6] Aggarwal HK, Mani MP, & Jacob M. MoDL: model-based deep learning architecture for inverse problems. IEEE Trans Med Imaging. 2019;38(2):394-405.

[7] Qi H, Hajhosseiny R, Cruz G, et al. End-to-end deep learning nonrigid motion-corrected reconstruction for highly accelerated free-breathing coronary MRA. Magn Reson Med. 2021;86:1983-1996.

[8] Pan J, Rueckert D, Küstner T, et al. Learning-based and unrolled motion-compensated reconstruction for cardiac MR cine imaging. In: Wang L, Dou Q, Fletcher PT, Speidel S, Li S (eds) Medical Image Computing and Computer Assisted Intervention – MICCAI 2022. MICCAI 2022. Lecture Notes in Computer Science, vol 13436. Springer, Cham.

[9] Scheffler K & Lehnhardt S. Principles and applications of balanced SSFP techniques. Eur Radiol. 2003;13:2409-2418.

Figures

Figure 1. Motion simulation and synthesis of the corrupted image. We assumed sinusoidal translation in each dimension and the motion starting point was randomly picked along the curve. The acquisition window was 160 ms considering a balanced steady-state free precession pulse sequence with a TR of 2 ms. Each TR the image was moved by the corresponding distance and Fourier transformed. The corresponding k-space line was acquired according to a random 4× undersampling mask, where the center was fully sampled. The bottom right is the synthesized undersampled and motion-corrupted image.

Figure 2. The unfolded variation network used for reconstruction. Each GD stage stands for one step of gradient descent optimization. The regularizer was a U-Net of two scales, and the motion estimator was a pair of three stacked convolutional layers with residual connections.

Figure 3. Reconstruction of the fat-suppressed coronal knee image. (A) The fully sampled reference image. (B) The 4× accelerated motion-corrupted image from zero-filled reconstruction. (C) Reconstruction using the variational network with no motion estimation module. The structural similarity (SSIM) was 39.30%, and the peak signal-to-noise ratio (PSNR) was 25.15 dB. (D) Reconstruction using the variational network with the motion estimation module. The SSIM was 49.43%, and the PSNR was 26.00 dB. The reconstructed image was sharper, and more details were recovered (arrows).

Figure 4. Reconstruction of the no fat-suppressed image. (A) The fully sampled reference image. (B) The 4× accelerated motion-corrupted image by zero-filled reconstruction. (C) Reconstruction using the variational network with no motion estimation module. The structural similarity (SSIM) was 68.12%, and the peak signal-to-noise ratio (PSNR) was 28.00 dB. (D) Reconstruction using the variational network with the motion estimation module. The SSIM was 69.53% and the PSNR was 27.98 dB. Similarly, the reconstructed image was sharper, and more details were recovered (arrows).

Table 1. Comparison of the reconstructed 500 slices of the testing set by structural similarity (SSIM) and peak signal-to-noise ratio (PSNR). The variational network with the motion estimation module achieved the best reconstruction results and was significantly better than those without using the motion estimation module. ME: motion estimation; VN: variational network.

Proc. Intl. Soc. Mag. Reson. Med. 31 (2023)

3106

DOI: https://doi.org/10.58530/2023/3106