Synopsis

Keywords: Image Reconstruction, Brain

Fast spin echo diffusion magnetic resonance imaging (FSE-DWI) is often referred to as a standard for MRI diagnosis of Cholesteatoma. However, the acquired data require multiple steps during image reconstruction which turn out high residual artifacts. In this work, we develop rapid reconstruction for propeller FSE-DWI to improve its signal-to-noise ratio (SNR) through unrolled deep learning (DL) framework. Results show that the proposed unrolled DL reconstruction enables increasing bout 2x SNR compared to SNR obtained by online reconstructed images. Moreover, its speed is about 200x faster than conventional locally low rank constraint reconstruction.

INTRODUCTION

Propeller fast spin echo diffusion magnetic resonance imaging (FSE-DWI)^1,2 is often referred to as a standard for MRI diagnosis of Cholesteatoma. However, the acquired data require multiple steps during image reconstruction which turn out high residual artifacts. In this work, we develop rapid reconstruction for propeller FSE-DWI to improve its signal-to-noise ratio (SNR) through unrolled deep learning framework.

MATERIALS and METHOD

Discreate single-blade signal model: A single-blade signal measured during readout $$$m\in[1\ M]$$$ of phase encoding line $$$n\in[1\ N]$$$ can be modeled as:
$$g_{c,α} [m,n]=∑_{p=1}^P∑_{q=1}^Qs_c [p,q]u[p,q] e^{(-j(k_{x.α} [m]p+k_{y,α} [n]q))}+ε_{c,α} [m,n] \quad (1)$$
where $$$p\in[1\ P]$$$ and $$$q\in[1\ Q]$$$ are pixel indices. $$$u$$$ is the complex-valued target image, $$$k_{x.α}$$$ and $$$k_{y.α}$$$ are the k-space coordinates in the readout and phase-encoding dimensions associated with blade angle $$$α\in[1\ N_α]$$$. $$$s_c$$$is the sensitivity profile for coil $$$c\in[1\ C]$$$, and $$$ε$$$ is white Gaussian noise. Defining $$$S=[diag\{S_1\}⋯diag\{S_C\}]^T\in C^{PQ×C}$$$, Eq. (1) abstracts to:
$$G_α=(I⨂F_α )Su_α+Ɛ_α=A_α u_α+Ɛ_α\quad(2)$$
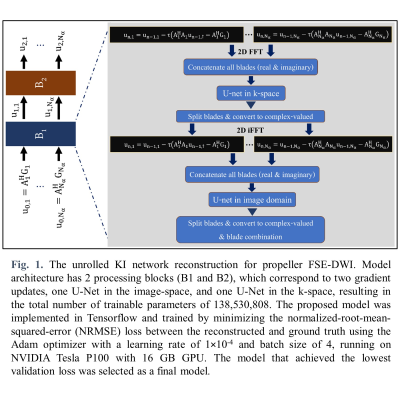
Reconstruction with Unrolled Network: To reconstruct set of underlying images from set of acquired k-space data, we solve the following optimization problem:
$$\min_{\{u_1,…,u_{N_α} ∈ C\}}\{R(u_1,…,u_{N_α})+\sum_{α=1}^{N_α}\parallel A_αu_α-G_α\parallel_2^2\} \quad (3)$$
where $$$R(·)$$$ is a regularization term that is modeled using multiple U-Nets³. Extending the KI-Net method in the RUN-UP⁴ to the propeller FSE-DWI, a reconstruction algorithm has two main components as described in Fig. 1. Note that 2X-oversampled type-II NUFFT in data consistency term was implemented through TFKBNUFFT⁵ with a width J=5 Kaiser-Bessel kernel.
Data Acquisition and Processing: In-vivo experiments were performed on 1.5T MRI (Ingenia; Philips, Best, the Netherlands) equipped with 12-channel receiver head coil. Twenty-one healthy volunteers and one patient with Cholesteatoma were scanned after informed consent according to institutional review board-approved (IRB) protocol. A vendor provided Propeller/Multivane FSE-DWI (b-value 0, and 3 directions of 1000 mm.2/sec.) was employed with following parameters: TR/TE = 2500/102 msec., FOV = 220x220 mm.2, readout samples 128, slice thickness 5 mm., 25 slices, 8 echo train lengths, 7 blades, SENSE-factor of 4, and scan time 2.10 minutes. In addition, coil sensitivity maps were estimated form single-shot FSE data using the ESPIRiT⁶. The ground-truth data were prepared using locally low rank (LLR)⁷ constraint reconstruction, performed on Matlab2015b with 30 iterations of FISTA with manually optimized β (β=0.03), block-size 7⨯7, 2X-oversampled type-II NUFFT with a width J=5 Kaiser-Bessel kernel. 1600 and 320 slices whole brain coverage from twenty healthy subjects and eight Cholesteatoma patients were used to train and validate the network, respectively. Data from one healthy subject and one patient were used for testing.

RESULTS

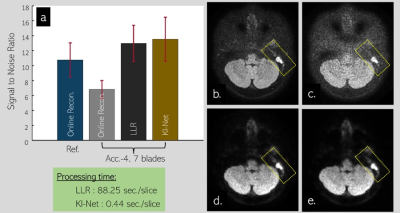
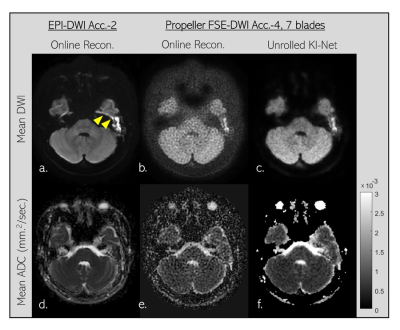
Fig. 2a shows mean±SD of SNR values of mean DWI images. SNR was calculated as ratio of mean to SD of image intensity inside the same ROI. 32 ROIs (100 pixels each) at white matter areas of one subject were manually selected and used for SNR calculation. The online reconstructed images corresponding to 2x under-sample with14 blades propeller FSE-DWI data is referred to as reference which has SNR values of 10.76±2.27. For 4x under-sample with 7 blades data, online reconstruction likely failed since images are highly corrupted by noise, thereby missing some small structures (yellow dashed box in image 2c). Not surprisingly, offline LLR can effectively suppress the noises, gaining about 2x SNR values higher than those values calculated from online reconstructed images (12.97±2.41 vs. 6.82±1.19). Likewise, offline LLR and unrolled KI-Net have mostly identical performance (12.97±2.41 vs. 13.52±2.94). SNR value of the unrolled KI-Net is slightly higher which may be due to smoothing effect that commonly occur on deep learning-based approach. This small effect is likely not a major concern since small structures inside inner ear are still well defined as shown in yellow dashed box of image 2e. In term of speed, the unrolled KI-Net is about 200 times faster than LLR method.
Fig. 3 demonstrates the advantage of propeller FSE-DWI over single shot EPI-DWI in patient with Cholesteatoma. Strong geometric distortion and signal pile-up at highly susceptible area can create an erroneous signa that looks like restricted-diffusion abnormality as pointed by yellow headed arrows (3a). Although propeller FSE-DWI can avoid such erroneous issue, online reconstructed image is likely not sufficient in quality due to high noise level. Luckily, unrolled KI-Net reconstruction enables to suppress the noise efficiently, improving the quality of mean DWI and mean appearance diffusion coefficient (ADC) as shown in 3c and 3f, respectively.

DISCUSSION

In this study, we developed a new reconstruction pipeline to improve image SNR and reconstruction speed for highly accelerated propeller FSE-DWI data. Non-uniform sampled forward model and its adjoint were implemented using tfkNUFFT that were unrolled through artificial neural network. Although the unrolled KI-Net is about 200 times faster than LLR method, some open questions should be investigated further. Firstly, rigid body motion caused by head movement should be included. Note that when motion parameters are given either retrospective or prospective fashions, the motion correction can be simply incorporated by updating k-space trajectories in the data consistency part without compromising the processing time. Secondly, other k-space based low rank approaches such as LORAKS⁸ and MUSSEL⁹ can be other potential techniques for the ground truth preparation. Lastly, the network can be further improved with large number of training data on both healthy volunteers and patients.

Acknowledgements

This study was financially supported by Chiang Mai University. We also thank Philips Healthcare Thailand to provide diffusion MRI sequence and other technical supports.