Introduction

Quantitative Susceptibility Mapping (QSM) quantifies the magnetic susceptibility distribution from the measured MRI phase information, but the ill-posed inversion process from phase to susceptibility limited its application. Recently, a few deep learning (DL) methods have been adopted for this problem with great performance, including end-to-end strategy^{1, 2} and model-based strategy^{3, 4}. However, current implementations of them are all based on a supervised learning scheme and the lack of the perfect golden standard for single-orientation in-vivo QSM hampers the tissue quantification accuracy.

In this work, we proposed a method, Self-Supervised Model-based QSM (SSMo-QSM), by combining the self-supervised strategy with model-based DL QSM reconstruction to reconstruct QSM by using the data itself without external data or multi-orientation data. By randomly separating data of the well-defined region in the frequency domain into data consistency part and loss part respectively, SSMo-QSM showed comparative performance and better generalization against supervised methods in synthetic datasets.

Methods

Pipeline
The linear field-to-susceptibility relationship in k-space can be formulated as:
$$\phi_k=D_k\mathcal{X}_k,\tag{1}$$ where $$$D_k$$$, $$$\phi_k$$$ and $$$\mathcal{X}_k$$$ represent the dipole kernel, normalized phase and susceptibility in k-space respectively.

In truncated k-space division (TKD)⁵, the dipole kernel is truncated by a threshold $$$\delta$$$ to prevent large incorrect values in direct division result $$$\widetilde{\mathcal{X}_k}=D_k^{-1}\phi_k$$$ and the remaining data at untruncated areas $$$M_k=(\left\lvert D_k\right\rvert>\delta)$$$ are kept as well-posed measured data $$$y=M_k\widetilde{\mathcal{X}_k}$$$. Thus, the ill-posed reconstruction problem can be transferred into an optimization problem with Fourier undersampling $$$\phi=M_k\mathcal{F}$$$:
$$\mathop{\arg\min}\limits_{\mathcal{X}}{\Vert\phi \mathcal{X}-y\Vert_2^2+\mathcal{R}(\mathcal{X})},\tag{2}$$ where $$$\mathcal{R}(\mathcal{X})$$$ represents the regularizer on susceptibility $$$\mathcal{X}$$$.

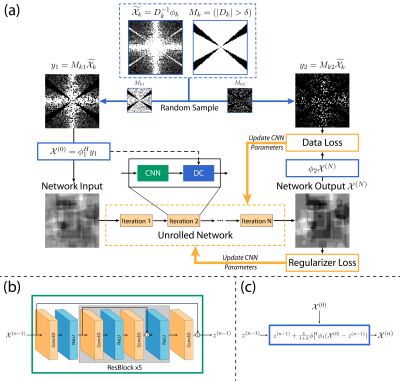
One solution of Eq. 2 is to alternate the optimization of $$$\mathcal{X}$$$ and the auxiliary variable $$$z$$$ iteratively, which is usually substituted by an unrolled network containing fixed numbers of CNN (Eq. 3) and DC (Eq. 4) blocks⁶:
$$z^{(n-1)}=f_{CNN}(\mathcal{X}^{(n-1)}),\tag{3}$$ $$\mathcal{X}^{(n)}=z^{(n-1)}+\frac{1}{1+\lambda}\phi^H\phi(\mathcal{X}^{(0)}-z^{(n-1)}).\tag{4}$$
For the supervised situation, a data loss function of MSE is calculated between network output $$$\mathcal{X}^{(N)}$$$ and the ground truth in k-space. The regularizer losses are also adopted for faster convergence, including a TV loss and a background loss based on the image domain background mask $$$m$$$. The total loss is written as:
$$L=\Vert\mathcal{F}\mathcal{X}^{(N)}-\mathcal{F}\mathcal{X}_{ref}\Vert_2^2+\mu_1TV(\mathcal{X}^{(N)})+\mu_2\Vert m\mathcal{X}^{(N)}\Vert_1\tag{5}$$ for CNN weights update.

Based on the pipeline mentioned above, SSMo-QSM is illustrated in Figure 1 with two randomly separated data sets without overlap with each other⁶. The set located by $$$M_{k1}$$$ is used for network input initiation and data consistency:
$$ \mathcal{X}^{(n)} = z^{(n-1)} + \frac{1}{1+\lambda} \phi_1^H \phi_1 (\mathcal{X}^{(0)} - z^{(n-1)}), \tag{6} $$ while the set located by $$$M_{k2}$$$ is used for loss calculation:
$$ L = \Vert \phi_2 \mathcal{X}^{(N)} - y_2 \Vert_2^2 + \mu_1 TV(\mathcal{X}^{(N)}) + \mu_2 \Vert m \mathcal{X}^{(N)} \Vert_1. \tag{7} $$
Implementation
The mask $$$M_{k1}$$$ used in the proposed self-supervised method is generated with uniform random selection within the 3d frequency domain, and $$$M_{k2} = M_{k} - M_{k1}$$$. The threshold $$$\delta$$$ for $$$M_k$$$ is 0.1, and the ratio of mask size $$$sum(M_{k1})/sum(M_{k})$$$ is set to 0.8.

The CNN adopted in the proposed pipeline is based on a ResNet-like structure, including 12 3D convolution layers with a kernel size of 3 and 32 channels. The iteration number N is 3.

Results

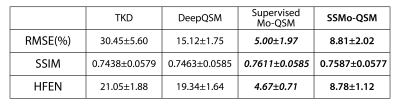
10000 64*64*64 3D synthetic susceptibility patches were simulated with randomly added cubes and spheres. The corresponding phase patches were generated according to Eq. 1 and the detailed configuration followed the description in DeepQSM². 9500 patches are used for training and the rest 500 patches are used for testing.

The proposed SSMo-QSM is compared with TKD and DeepQSM. To better analyze the influence of the self-supervised strategy, the supervised pipeline (captioned as Supervised Mo-QSM) described in Methods part is also compared.

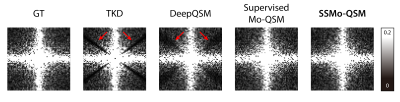
Figure 2 shows one example of the predicted susceptibility map with different reconstruction methods in the plane parallel to $$$B_0$$$ and perpendicular to $$$B_0$$$. Figure 3 shows the quantitative performance metrics compared between different reconstruction methods. The results suggested that the Supervised Mo-QSM shows the best reconstruction performance on susceptibility mapping and artifact reduction, while SSMo-QSM exhibits comparable performance to the supervised Mo-QSM. In comparison, DeepQSM suffered severe susceptibility underestimation and TKD results are polluted by background bias and streaking artifacts.

Figure 4 shows the frequency domain of the reconstructed susceptibilities by different methods. Compared with the ground truth, both Supervised Mo-QSM and SSMo-QSM show similar results, while the TKD and DeepQSM suffer obvious data loss at the truncated areas.

Figure 5 gives the generalization test results with a different resolution from the training data. Visually, SSMo-QSM shows less streaking artifact than the results reconstructed using the Supervised Mo-QSM, DeepQSM and TKD.

Discussion

The results on synthetic data showed that the proposed SSMo-QSM achieved a comparable result with the Supervised MoQSM, while outperforming the conventional TKD and the end-to-end learning method DeepQSM. The k-pace comparison results and generalization test further confirmed the effectiveness of the model-based network architecture in recovering the loss information at the truncated areas of TKD, and also the effectiveness of the self-supervised strategy for QSM reconstruction with better generalization.

Conclusion

In conclusion, the proposed learning-based SSMo-QSM shows great potential for accurate QSM reconstruction without ground truth. Further studies are needed to validate the self-supervised strategy in realistic in-vivo QSM reconstruction.

Acknowledgements

No acknowledgement found.