3090
4D Cardiac MR Image Reconstruction by Deep Learning with Wavelet Transform1Laboratory of Biomedical Imaging and Signal Processing, the University of Hong Kong, HongKong, China, 2Department of Electrical and Electronic Engineering, the University of Hong Kong, HongKong, China, 3Department of Electrical and Electronic Engineering, Southern University of Science and Technology, Shenzhen, China
Synopsis
Keywords: Data Analysis, Cardiovascular, cardiac reconstruction,deep learning
We present a CNN-based deep learning model to reconstruct the cardiac cine images from undersampled single-channel 4D MR data. The wavelet transform and spatial-temporal attention mechanisms are introduced in the model. The proposed model could reconstruct the cardiac images and recover the cardiac wall motion more robustly than the low-rank plus sparsity (i.e., L+S) reconstruction method. This approach presents one promising solution for accelerated cardiac dynamic imaging with one single channel through deep learning from the sparsity in spatial and temporal domains.Introduction
Dynamic MRI plays a critical part in clinical applications due to the capability of simultaneously revealing the spatial structures and their dynamic changes with time. However, the competition between spatial and temporal resolution exists in practice for a fixed scan time. Thus it is imperative to accelerate dynamic imaging through undersampling k-space and t-space. Sparsity underlying the data (e.g., cardiac cine data) is explored1,2 but the selection of the sparse transform and the relevant regularization parameters either locally or globally still requires careful tunings. Here, we present one 2D spatial plus 1D time (2D+1D) deep learning model with an attention mechanism to explore the spatial sparsity with the wavelet transform3 embedded in the model and the temporal sparsity with the 1D convolution operations. The model is trained using fully sampled multi-slice multi-phase single-channel cardiac data.Methods
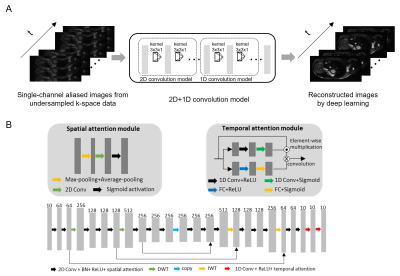
Figure 1A shows the proposed deep learning model with the input as the 2D+1D aliased images reconstructed from undersampled k-space data and output as the unaliased 2D+1D target images. Specifically, a CNN-based deep learning 2D+1D model is designed to explore spatial sparsity by integrating wavelet transform into the 2D convolution and to sequentially explore temporal sparsity by 1D convolution (Figure 1B). The attention mechanism is used in the model for exploiting the correlation in both spatial and temporal domains4,5.The training and testing data were from the publicly available OCMR public database6. They were 28-channel multi-slice multi-phase fully sampled 1.5T cardiac data from 8 subjects acquired using SSFP sequence with matrix size 320x120, slice number 12, 10 cardiac phases, and TR/TE=28.5/1.4ms. Coil compression was used to compress the multi-channel data to a single channel7. Data were retrospectively undersampled (uniformly in in-plane phase encoding direction) with undersampling patterns linearly interleaving between adjacent cardiac phases for training (7 subjects) and testing 1 (1 subject). Note that a single model was trained and applied to all individual 2D slices.
Adam optimizer8 was carried out for training with β1 = 0.9, β2 = 0.999, and initial learning rate = 0.0001. The training was conducted on a Geforce RTX 3090 GPU using PyTorch 1.8.1 package9 with a batch size of 5 and 150 epochs. The total training time was approximately 17.5 hrs. For evaluation, we compared the deep learning results with reconstructed images from the low-rank plus sparsity (i.e., L+S) reconstruction method2 qualitatively and quantitatively using PSNR10 and NRMSE11.
Results
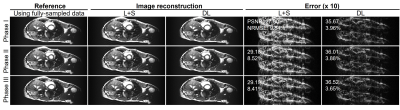
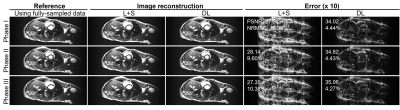
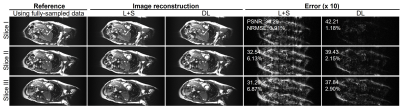
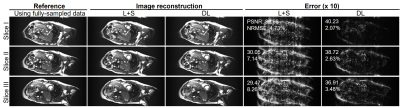
Figure 2 shows the typical reconstructed images at the same location but three different cardiac phases at acceleration factor R = 2 from one subject. Quantitatively, the reconstructed images using the proposed deep learning have higher PSNR and lower NRMSE values than those using the existing L+S method. Figure 3 presents the reconstructed images at R = 3 from the same dataset as used in Figure 2. The reconstruction performance using the deep learning model was observed to be consistently better than that using the L+S method. These results indicate that our deep learning model could well reconstruct the cardiac cine images. Figure 4 shows the reconstructed images at the same phase but in different locations at R = 2 from the same subject. The deep learning model could reconstruct the images better than the L+S method and simultaneously recover the cardiac wall motion well. Figure 5 shows the results corresponding to Figure 4 but at R = 3. The reconstruction performance of the deep learning model was seen to consistently outperform that of the L+S method. These results demonstrated that our method could robustly reconstruct the cardiac cine images from uniformly undersampled single-channel data= and well recover the cardiac wall motion.Discussion and Conclusions
The proposed deep learning model enables robust end-to-end single-channel cardiac cine image reconstruction by exploring the inherent data sparsity in the spatial and temporal domains. Sometimes low-cost or/and low-field MR scanners can only have one receiving coil (i.e., single-channel), thus it is imperative to advance imaging acceleration under the hardware limitation of one coil. In this study, we propose a 2D+1D model that is relatively simple but robust. It separately deals with temporal and spatial sparsity, which alleviates the model complexity and facilitates its training when compared with a truly 3D model that simultaneously focuses on both temporal and spatial sparsity. With the temporal attention module, our proposed model utilizes the information from the same slice but different cardiac phases. Meanwhile, the wavelet transform and spatial attention module efficiently take advantage of the data sparsity in the spatial domain.Acknowledgements
This work was supported in part by Hong Kong Research Grant Council (R7003-19F, HKU17112120, HKU17127121 and HKU17127022 to E.X.W., and HKU17103819, HKU17104020 and HKU17127021 to A.T.L.L.), Lam Woo Foundation, and Guangdong Key Technologies for AD Diagnostic and Treatment of Brain (2018B030336001) to E.X.W..References
[1] Huang W, Ke Z, Cui Z-X, Cheng J, Qiu Z, Jia S, Ying L, Zhu Y, Liang D. Deep low-rank plus sparse network for dynamic MR imaging. Medical Image Analysis 2021;73:102190.
[2] Otazo R, Candes E, Sodickson DK. Low‐rank plus sparse matrix decomposition for accelerated dynamic MRI with separation of background and dynamic components. Magnetic Resonance in Medicine 2015;73(3):1125-1136.
[3] Mallat S. A wavelet tour of signal processing: Elsevier; 1999.
[4] Liu Z, Wang L, Wu W, Qian C, Lu T. Tam: Temporal adaptive module for video recognition. In: Proceedings of the IEEE/CVF International Conference on Computer Vision, 2021, p 13708-13718. [5] Woo S, Park J, Lee J-Y, Kweon IS. Cbam: Convolutional block attention module. In: Proceedings of the European conference on computer vision (ECCV), 2018, p 3-19.
[6] Chen C, Liu Y, Schniter P, Tong M, Zareba K, Simonetti O, Potter L, Ahmad R. OCMR (v1. 0)--Open-Access Multi-Coil k-Space Dataset for Cardiovascular Magnetic Resonance Imaging. arXiv preprint arXiv:200803410 2020.
[7] Zhang T, Pauly JM, Vasanawala SS, Lustig M. Coil compression for accelerated imaging with Cartesian sampling. Magnetic Resonance in Medicine 2013;69(2):571-582.
[8] Kingma DP, Ba J. Adam: A method for stochastic optimization. arXiv preprint arXiv:14126980 2014.
[9] Paszke A, Gross S, Massa F, Lerer A, Bradbury J, Chanan G, Killeen T, Lin Z, Gimelshein N, Antiga L. Pytorch: An imperative style, high-performance deep learning library. Advances in neural information processing systems 2019;32.
[10] Hore A, Ziou D. Image quality metrics: PSNR vs. SSIM. In: 2010 20th international conference on pattern recognition, 2010, IEEE, p 2366-2369.
[11] da Costa-Luis CO, Reader AJ. Micro-networks for robust MR-guided low count PET imaging. IEEE transactions on radiation and plasma medical sciences 2020;5(2):202-212.
Figures