3081
Unsupervised denoising of prostate DWI
Laura Pfaff1,2, Fabian Wagner1, Julian Hossbach1,2, Elisabeth Preuhs1, Fasil Gadjimuradov1,2, Thomas Benkert2, Dominik Nickel2, Tobias Wuerfl2, and Andreas Maier1
1Pattern Recognition Lab, Friedrich-Alexander-Universität Erlangen-Nürnberg, Erlangen, Germany, 2Magnetic Resonance, Siemens Healthcare GmbH, Erlangen, Germany
1Pattern Recognition Lab, Friedrich-Alexander-Universität Erlangen-Nürnberg, Erlangen, Germany, 2Magnetic Resonance, Siemens Healthcare GmbH, Erlangen, Germany
Synopsis
Keywords: Image Reconstruction, Diffusion/other diffusion imaging techniques
The diagnostic value of diffusion-weighted MR images is often degraded by their inherently low signal-to-noise ratio (SNR), especially for high b-values. In this context, the application of learning-based denoising methods is difficult since most methods require noise-free target images for training. We show how to denoise and evaluate diffusion-weighted MR images in a self-supervised manner by exploiting an adapted version of Stein’s unbiased risk estimator and specific properties of the data. Both quantitative and qualitative evaluations indicate increased performance over state-of-the-art unsupervised denoising methods.Introduction
Diffusion-weighted imaging (DWI) is an important tool for detecting and characterizing lesions. However, one major drawback of DWI is that the images, especially those acquired with higher b-values, suffer from inherently low signal-to-noise ratio (SNR) due to the diffusion weighting and long echo times necessary to accommodate the additional gradient pulses1. As a result, in some body regions such as the prostate, individual repetitions are hardly usable for diagnosis. The state-of-the-art practice is to acquire repeated acquisitions and compute an average over these repetitions to improve SNR. However, acquiring many repetitions is time-consuming and the averaged result is prone to motion artifacts. Therefore, the number of repetitions and thus the improvement of the SNR is limited. In this work, we show how to leverage the redundancy in repeated acquisitions for self-supervised denoising using deep learning and an extended version of Stein's unbiased risk estimator (SURE)2.Methods
SURE was first proposed by Charles Stein in 1981 and provides a statistical method to estimate the mean squared error (MSE) between the unknown mean $$$\boldsymbol{x}$$$ of a Gaussian distributed signal $$$\boldsymbol{y}$$$ and its estimate $$$\hat{\boldsymbol{x}}=\boldsymbol{f}(\boldsymbol{y})$$$. This can be adapted to an image denoising problem as shown by Metzler et al.3. Here, the goal is to reconstruct an unknown noise-free image $$$\boldsymbol{x}$$$ corrupted by Gaussian noise $$$\boldsymbol{\eta}$$$ from a noisy image $$$\boldsymbol{y}=\boldsymbol{x}+\boldsymbol{\eta}$$$. Since the noise is additive and has zero mean, the unknown noise-free image $$$\boldsymbol{x}$$$ can be considered as the mean vector of the noisy image $$$\boldsymbol{y}$$$.The original SURE expression assumed the presence of spatially invariant Gaussian noise. To properly address the spatially variant noise enhancement in reconstructed MR images, we use an adapted SURE approach that incorporates a noise map $$$\boldsymbol{\sigma}$$$ indicating the standard deviation of the noise for every pixel as proposed in4.
Consequently, SURE can be used as a loss function to train a neural network $$$\boldsymbol{f}(\boldsymbol{y})$$$ that receives noisy measurements $$$\boldsymbol{y}$$$ as input and predicts an estimate of $$$\boldsymbol{x}$$$ as output by minimizing SURE, i.e., the estimated MSE as follows:
$$\frac{1}{D}\parallel\boldsymbol{f}(\boldsymbol{y})-\boldsymbol{x}\parallel^{2}=\frac{1}{D}\parallel \boldsymbol{f}(\boldsymbol{y})-\boldsymbol{y}\parallel^{2}-\frac{1}{D}\sum\nolimits_{d=1}^D\sigma_d^2+\frac{2}{D}\sum\nolimits_{d=1}^D\sigma_d^2\frac{\partial f_d (\boldsymbol{y})}{\partial y_d} ,$$
where D is the number of pixels.
Considering that SURE cannot be applied to magnitude averages due to their non-Gaussian noise distribution, we performed a phase correction as described on the individual repetitions5. This allows us to compute averages over the complex-valued images without signal loss while also preserving the zero-centered Gaussian noise distribution. Representative results are illustrated in Figure 1.
Since multiple repetitions are acquired for each slice and diffusion direction, the required spatially resolved noise map $$$\boldsymbol{\sigma}$$$ incorporated in the SURE loss can simply be generated by calculating the standard deviation between the repetitions for each pixel, as shown in Figure 2.
A total of 319 prostate image volumes with a b-value of 800 and four diffusion directions with ten repetitions each were acquired from volunteers using various 1.5 and 3 T scanners (MAGNETOM, Siemens Healthcare, Erlangen, Germany) and standard acquisition protocols.
The DnCNN-based architecture6 in Figure 3 was implemented in PyTorch and trained with images from 4,073 slices using SURE as an unsupervised loss function. Images of the four different diffusion directions were denoised separately before calculating the trace image via geometric mean. We compare our method with two state-of-the-art unsupervised denoising methods: the deep-learning-based approach Noise2Noise7, as well as the non-learning-based approach BM3D8.
To be able to quantitatively compare the results of the different methods, we calculated estimates of the MSE and peak signal-to-noise-ratio (PSNR) between the denoised images and the original images for 1,349 test slices without access to noise-free ground-truth images using SURE as a substitute for the MSE.
Results and Discussion
The SURE-based quantitative evaluation results are presented in Table 1. Representative result images of the different methods are shown in Figure 4. Based on the quantitative results, our method performs considerably better than the state-of-the-art unsupervised denoising methods Noise2Noise and BM3D. It is important to note that due to the lack of ground truth, the presented results are SURE-based estimates of the actual metrics. However, in cases where the noise model can be determined precisely this estimate is very accurate. The quantitative findings are further supported by the representative result images. While Noise2Noise and BM3D tend to produce over-smoothed images, the results obtained with SURE appear less blurred and retain structures that may be anticipated from the noisy input.Conclusion
We demonstrated how to perform learning-based fully self-supervised denoising in prostate DWI, outperforming established denoising methods like BM3D. However, the proposed approach is not limited to prostate DWI but can also be applied to other body regions. Our method can be used to either improve the image quality by increasing the SNR with the same number of repetitions or to reach equivalent image quality with fewer repetitions, resulting in reduced scan time.Acknowledgements
No acknowledgement found.References
- Kitajima K, Kaji Y, Kuroda K et al. High b-value diffusion-weighted imaging in normal and malignant peripheral zone tissue of the prostate: effect of signal-to-noise ratio. Magn Reason Med Sci 2008; 7(2):93-99.
- Stein C. Estimation of the mean of a multivariate normal distribution. The Annals of Statistics 1981; 9(6):1135–1151.
- Metzler C, Mousavi A, Heckel R et al. Unsupervised learning with Stein’s unbiased risk estimator. arXiv preprint arXiv:1805.10531, 2018.
- Pfaff L, Hossbach J, Preuhs E et al. Training a tunable, spatially adaptive denoiser without clean targets. In Proceedings of the joint annual meeting ISMRM-ESMRMB, 2022.
- Prah DE, Paulson ES, Nencka AS et al. A simple method for rectified noise floor suppression: Phase-corrected real data reconstruction with application to diffusion-weighted imaging. Magn Reson Med 2010; 64(2):418-29.
- Zhang K, Zuo W, Chen Y et al. Beyond a Gaussian denoiser: residual learning of deep CNN for image denoising. IEEE Transactions on Image Processing 2017; 26(7):3142-3155.
- Lehtinen J, Munkberg J, Hasselgren J et al. Noise2noise: Learning image restoration without clean data. arXiv preprint arXiv:1803.04189, 2018.
- Song B, Duan Z, Gao Y et al. Adaptive BM3D algorithm for image denoising using coefficient of variation. In 2019 22nd International Conference on Information Fusion (FUSION) 2019; 1–8.
Figures
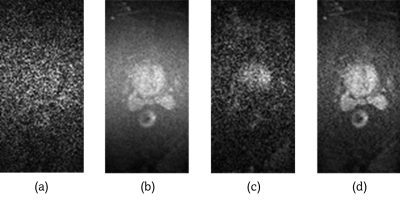
Figure 1: Image (a) shows an individual repetition of a
diffusion-weighted prostate scan with a b-value of b=800. Image (b) shows the
result after performing magnitude averaging over the 10 repetitions for each of
the 4 diffusion directions, (c) is the result after complex averaging without
phase correction, and (d) illustrates the improved result of complex averaging
with phase correction.
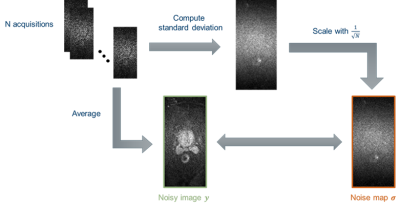
Figure 2: The noise map is calculated by computing the
standard deviation between the N repetitions. It is then divided by the square
root of the number of repetitions to account for the averaging operation.
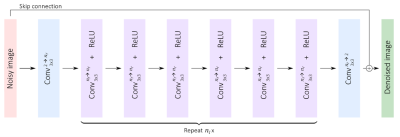
Figure 3: The used network architecture resembles a
DnCNN, consisting of repetitions of convolutional layers paired with ReLU
activations as well as a global skip connection.
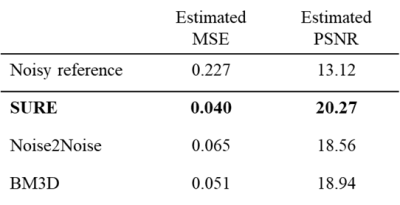
Table 1: Quantitative results for the different
methods have been estimated using SURE. As can be seen, SURE outperforms both
Noise2Noise and BM3D in terms of MSE and PSNR. Noisy reference refers to the
reference calculation between the noisy input images and the ground truth.
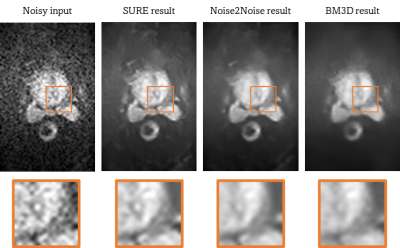
Figure 4: Result
images of the different methods with magnified ROIs. The first image shows the
noisy input image, while the second image is the denoised result using the
proposed SURE-based method. The results of the reference methods Noise2Noid and
BM3D are illustrated in the third and fourth images.
DOI: https://doi.org/10.58530/2023/3081