3076
CNN-based Estimation of Spatio-Temporal Regularization Parameter-Maps for TV-Reconstruction in Dynamic Cardiac MRI1Physikalisch-Technische Bundesanstalt (PTB), Braunschweig and Berlin, Germany, 2Weierstraß-Institut für Angewandte Analysis und Stochastik, Berlin, Germany, 3King’s College London, London, United Kingdom, 4Technische Universität Berlin, Berlin, Germany, 5Humboldt Universität zu Berlin, Berlin, Germany, 6Science and Technology Facilities Council (STFC), Oxford, United Kingdom, 7Finden Ltd, Oxford, United Kingdom, 8Queen Mary University of London, London, United Kingdom
Synopsis
Keywords: Image Reconstruction, Machine Learning/Artificial Intelligence, Interpretable Machine Learning, Algorithmic Unrolling, Iterative Neural Networks
We propose a method for estimating spatio-temporal regularization parameter-maps to be used for dynamic cardiac MR image reconstruction using total variation (TV)-minimization. Based on recent developments in algorithmic unrolling using Neural Networks (NNs), our approach uses two sub-networks. The first one predicts a spatio-temporal regularization parameter-map from an input image. Then, a second sub-network approximately solves a TV-reconstruction problem which is formulated with the estimated regularization parameter-map. We show that the proposed method can be used to further improve the TV-reconstructions compared to using only one single scalar regularization parameter or two regularization parameters for space and time.
Introduction
Nowadays, methods based on deep unrolled Neural Networks (NNs)1 define the state-of-the-art in image reconstruction2,3,4. These NNs are constructed to resemble iterative schemes of finite length in which the parameters of the regularizers can be trained in a supervised manner. However, the black-box character of the regularizers when given as deep NNs poses a challenge for their clinical application, especially since some studies have shown NNs to be possibly unstable compared to classical methods5.In contrast, reconstruction methods based on hand-crafted regularization techniques such as Wavelets6 or total variation (TV)7 come with well-understood mathematical theory, convergence guarantees and interpretability. Thereby, the choice of the regularization parameter which balances between the data-fidelity and the regularization plays a crucial role.
Having only one scalar regularization parameter $$$\lambda>0$$$ which globally imposes the regularization can be sub-optimal. For dynamic cardiac MRI applications, for example, the temporal dimension is the one which offers the greatest potential to exploit the sparsity ofthe image in its gradient domain. However, a careful choice is required in order to maintain the diagnostic image-content, i.e. the cardiac motion.
Moreover, it might be desirable to choose the strength of the regularization based on the local image content depending on the specific clinical application. Methods for choosing voxel-dependent regularization parameter-maps based on the solution of bi-level optimzation problems have beenproposed in the literature8,9,10 but are typically too time-consuming for the clinical application.
In this work, we propose to employ NNs for the fast estimation of task-specific and patient-dependent regularization parameter-maps which can be used for TV-based reconstruction in dynamic cardiac MRI.
Methods
The data-acquisition is given by$$\mathbf{y} = \mathbf{A}\mathbf{x} + \mathbf{e}, \hspace{3cm} (1)$$
where $$$\mathbf{A}$$$ denotes the MRI-operator, $$$\mathbf{x} \in \mathbb{C}^N, N=N_x \cdot N_y \cdot N_t,$$$ a complex-valued cine MR-image, $$$\mathbf{y} \in \mathbb{C}^{N_c \cdot M}, M<N,$$$ the undersampled, noisy multi-coil dynamic $$$k$$$-space data and $$$\mathbf{e}$$$ Gaussian noise with standard deviation $$$\sigma>0$$$ .
Using a single scalar $$$\lambda>0$$$ or two distinct scalars $$$\lambda_{xy}, \lambda_t>0$$$ for space and time, the TV-minimization problems are given by
$$\underset{\mathbf{x}}{\min} \frac{1}{2} \| \mathbf{A}\mathbf{x} - \mathbf{y}\|_2^2 + \lambda \| \nabla \mathbf{x}\|_1 \hspace{3cm} (2)$$
and
$$\underset{\mathbf{x}}{\min} \frac{1}{2} \| \mathbf{A}\mathbf{x} - \mathbf{y}\|_2^2 + \lambda_{xy} \| \nabla_{xy} \mathbf{x}\|_1 + \lambda_{t} \| \nabla_{t} \mathbf{x}\|_1 \hspace{3cm} (3)$$
respectively, where $$$\nabla:=[\nabla_x, \nabla_y, \nabla_t]^{\scriptstyle \boldsymbol{\mathsf{T}}}$$$ and $$$\nabla_{xy}:=[\nabla_x, \nabla_y]^{\scriptstyle \boldsymbol{\mathsf{T}}}$$$.
Imposing a spatio-temporal and voxel-dependent regularization can be achieved by formulating the problem as
$$\underset{\mathbf{x}}{\min} \frac{1}{2} \| \mathbf{A}\mathbf{x} - \mathbf{y}\|_2^2 + \| \boldsymbol{\Lambda} \nabla \mathbf{x}\|_1 \hspace{3cm} (4)$$
where is $$$\boldsymbol{\Lambda}$$$ is a diagonal operator with strictly positive entries which weights the $$$\ell_1$$$-norm. Problems (2), (3) and (4) can be solved with well-known methods from the literature, e.g. the primal dual hybrid gradient (PDHG) algorithm11.
Our proposed method (NN-PDHG) consists of an unrolled NN with two distinct sub-networks. The first sub-network - a simple 3D U-Net12 - estimates a regularization parameter-map from an input image. The second sub-network unrolls $$$T$$$ steps of PDHG to obtain an (approximate) solution of problem (4). All parameters of the entire network can be otbained by supervised end-to-end training on a set of input-target image-pairs. The regularization parameter-map is constrained to be component-wise in the interval $$$(0,C)$$$ with $$$C>0$$$. Figure 1 shows a schematic illustration of the proposed method.
We applied and evaluated the method on a dynamic cardiac MRI reconstruction problem. The dataset consisted of 216 cine MR images13 of shape $$$160\times 160 \times 30$$$ which we split into portions of 144/36/36 images for training, validation and testing.
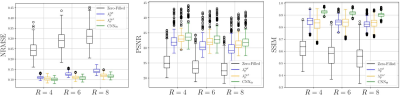
We trained the networks for 200 epochs using the mean squared-error (MSE) as a loss-function using the ADAM optimizer with an initial learning rate of $$$10^{-4}$$$. We compared the proposed NN-PDHG method to the reconstructions which can be obtained by PDHG by solving (2) and (3) for three different acceleration factors $$$R=4,6,8$$$, noise-level $$$\sigma=0.3$$$ and $$$N_c=12$$$ coils. All methods were compared in terms of PSNR, NRMSE and SSIM13.
Results
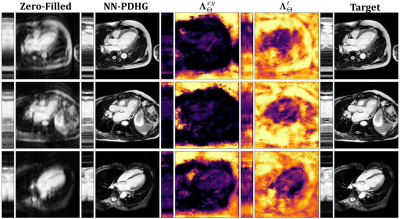
Figure 2 shows results obtained with NN-PDHG using the regularization parameter-map obtained with the proposed CNN for $$$R=4,6,8$$$ . In all cases, the proposed method improved the results, especially in terms of SSIM, which is best visible from the box-plots in Figure 3. Figure 4 shows examples of the regularization parameter-maps for $$$R=6$$$.Discussion
With the proposed approach, it is possible to further improve the well-known TV-minimization based reconstruction. In Figure 4, we clearly see that the network naturally attributes different meanings to the spatial and the temporal directions. The temporal component of $$$\boldsymbol{\Lambda}_{\Theta}$$$ tends to have higher values compared to the spatial one, especially in regions where no cardiac motion is visible. Further, by assigning smaller values in regions covering the heart, the network seems to prefer to maintain a higher data-fidelity.Note that, although the choice of the regularization parameter-map is data-driven and based on NNs (hence a black-box), the reconstruction is entirely interpretable and inherits all convergence properties from the respective PDHG-algorithm.
Conclusion
In this work, we have proposed a method which combines NNs and model-based image reconstruction. The approach is simple and efficient and can be used to estimate patient-adaptive regularization parameter-maps. Although presented for a dynamic cardiac MRI reconstruction problem, the method is flexible and we expect it to be applicable to different regularization methods and imaging problems.Acknowledgements
The authors acknowledge the support of the Berlin Mathematics Research Center MATH+ (EXC-2046/1, project ID: 390685689) as this work was initiated during the Hackathon event “Maths Meets Image”, Berlin, March 2022, which was part of the MATH+ Thematic Einstein Semester on “Mathematics of Imaging in Real-World Challenges".
This work was funded by the UK EPSRC grants "Computational Collaborative Project in Synergistic PET/MR Reconstruction" (CCP PETMR) EP/M022587/1 and its associated Software Flagship project EP/P022200/1; the "Computational Collaborative Project in Synergistic Reconstruction for Biomedical Imaging" (CCP SyneRBI) EP/T026693/1; "A Reconstruction Toolkit for Multichannel CT" EP/P02226X/1 and "Collaborative Computational Project in tomographic imaging’' (CCPi) EP/M022498/1 and EP/T026677/1. This work made use of computational support by CoSeC, the Computational Science Centre for Research Communities, through CCP SyneRBI and CCPi.
This work is part of the Metrology for Artificial Intelligence for Medicine (M4AIM) project that is funded by the Federal Ministery for Economic Affairs and Energy (BMWi) in the frame of the QI-Digital initiative.
References
1. Monga, V., Li, Y., & Eldar, Y. C. (2021). Algorithm unrolling: Interpretable, efficient deep learning for signal and image processing. IEEE Signal Processing Magazine, 38(2), 18-44.
2. Schlemper, J., Caballero, J., Hajnal, J. V., Price, A., & Rueckert, D. (2017, June). A deep cascade of convolutional neural networks for MR image reconstruction. In International conference on information processing in medical imaging (pp. 647-658). Springer, Cham.
3. Hammernik, K., Klatzer, T., Kobler, E., Recht, M. P., Sodickson, D. K., Pock, T., & Knoll, F. (2018). Learning a variational network for reconstruction of accelerated MRI data. Magnetic resonance in medicine, 79(6), 3055-3071.
4. Aggarwal, H. K., Mani, M. P., & Jacob, M. (2018). MoDL: Model-based deep learning architecture for inverse problems. IEEE transactions on medical imaging, 38(2), 394-405.
5. Antun, V., Renna, F., Poon, C., Adcock, B., & Hansen, A. C. (2020). On instabilities of deep learning in image reconstruction and the potential costs of AI. Proceedings of the National Academy of Sciences, 117(48), 30088-30095.
6. Chaâri, L., Pesquet, J. C., Benazza-Benyahia, A., & Ciuciu, P. (2011). A wavelet-based regularized reconstruction algorithm for SENSE parallel MRI with applications to neuroimaging. Medical image analysis, 15(2), 185-201.
7. Block, K. T., Uecker, M., & Frahm, J. (2007). Undersampled radial MRI with multiple coils. Iterative image reconstruction using a total variation constraint. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine, 57(6), 1086-1098.
8. Hintermüller, M., & Papafitsoros, K. (2019). Generating structured nonsmooth priors and associated primal-dual methods. In Handbook of numerical analysis (Vol. 20, pp. 437-502). Elsevier.
9. Calatroni, L., Cao, C., De Los Reyes, J. C., Schönlieb, C. B., & Valkonen, T. (2017). Bilevel approaches for learning of variational imaging models. Variational Methods: In Imaging and Geometric Control, 18(252), 2.
10. De los Reyes, J. C., & Villacís, D. (2022). Bilevel Optimization Methods in Imaging. In Handbook of Mathematical Models and Algorithms in Computer Vision and Imaging: Mathematical Imaging and Vision (pp. 1-34). Cham: Springer International Publishing.
11. Chambolle, A., & Pock, T. (2011). A first-order primal-dual algorithm for convex problems with applications to imaging. Journal of mathematical imaging and vision, 40(1), 120-145.
12. Hauptmann, A., Arridge, S., Lucka, F., Muthurangu, V., & Steeden, J. A. (2019). Real‐time cardiovascular MR with spatio‐temporal artifact suppression using deep learning–proof of concept in congenital heart disease. Magnetic resonance in medicine, 81(2), 1143-1156.
13. Kolbitsch, C., Prieto, C., &
Schaeffter, T. (2014). Cardiac functional assessment without
electrocardiogram using physiological self‐navigation. Magnetic resonance in medicine, 71(3), 942-954.
Figures

Figure 1: The proposed NN-PDHG approach. The first sub-network estimates a spatio-temporal regularization parameter-map $$$\boldsymbol{\Lambda}_{\Theta} = (\boldsymbol{\Lambda}_{\Theta}^{xy}, \boldsymbol{\Lambda}_{\Theta}^{xy}, \boldsymbol{\Lambda}_{\Theta}^{t})$$$ which is used within the second sub-network which unrolls $$$T$$$ iterations of PDHG for (approximately) solving the TV-minimization problem (4).
The first sub-network's parameters are trained such that the outputs of the second sub-network are close to the target images.
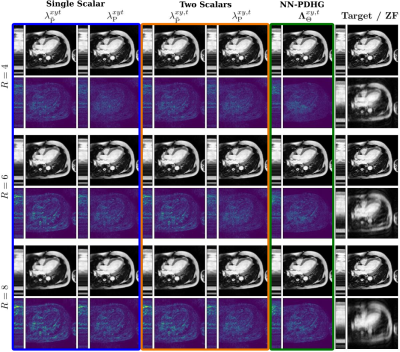
Figure 2: An example of images reconstructed for $$$R=4,6,8$$$ with different choices of regularization parameters. From left to right for each row: Single scalar $$$\lambda_{\tilde{P}}^{xyt}>0$$$ and $$$\lambda_{P}^{xyt}>0$$$, two scalars $$$\lambda_{\tilde{P}}^{xy,t}>0$$$ and $$$\lambda_{P}^{xy,t}>0$$$ for space and time and the proposed parameter-map $$$\boldsymbol{\Lambda}_{\Theta}$$$. Thereby, $$$\tilde{P}$$$ and $$$P$$$ denote "best over a training set" or "best for the respective image" (obtained by grid search), respectively.