Synopsis

Keywords: Data Processing, Permeability

Filter exchange imaging (FEXI) is a promising technique for measuring water exchange across the blood-brain barrier (BBB). However, the application of FEXI for the rodent brain requires thinner slices and therefore higher crusher gradients which lead to a progressive underestimation of the apparent exchange rate (AXR). Here, we implement a crusher-compensated exchange rate (CCXR) model which reduces the bias induced by the crusher gradients and allows more accurate estimates of BBB water exchange in the rat brain.

INTRODUCTION

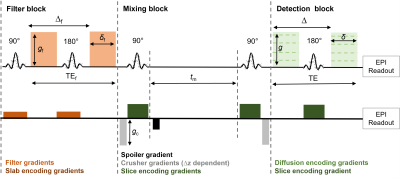
Filter exchange imaging (FEXI) is a promising technique to measure water exchange across the blood-brain barrier (BBB; termed BBB-FEXI) in the human brain [1, 2]. The implementation of BBB-FEXI in the rodent brain would permit controlled studies of disease using transgenic models. However, the markedly smaller rodent brain requires thinner imaging slices. The minimum required magnitude of the crusher gradients in the FEXI sequence increases for thinner slices (Figure 1). Previously, Lasič et al. demonstrated that high crusher gradient magnitudes cause an underestimation of the apparent exchange rate (AXR) [3]. These effects are exacerbated when using low filter b-values and biases are greater for low BBB exchange rates. Therefore, there is a need to explore extended signal models which are able to compensate for the effects of the crusher gradients, facilitating the use of thinner imaging slices needed for accurate BBB water exchange estimates in the rodent brain.

METHODS

Simulations
To investigate the impact of crusher gradients on ADC'(t_m) and ADC^eq(t_m) at three slice thicknesses ∆z = 2.5, 4.0 and 10.0 mm, synthetic signals incorporating the effects of crusher gradients were generated in Matlab R2021a using a two-compartment model [3]. Input parameters: water exchange rate, k_in = 2.38 s^-1, k = k_in + k_out = AXR = 2.5 s^-1 [4], intravascular volume fraction f_i = 0.05, intravascular and extravascular diffusivities, D_i = 6.5 x 10^-3 mm²/s and D_e = 0.65 x 10^-3 mm²/s respectively [5]. Signals were simulated with the filter block switched on and switched off (b_f = 250 and 0 s/mm² respectively) at mixing times, t_m = 0.025, 0.05, 0.1, 0.2 and 0.3 s. The detection block was simulated with eight readout b-values, b = 0, 25, 54, 116, 250, 539, 1160, 2500 s/mm².

In vivo acquisition & analysis
To confirm simulated effects ­in vivo at ∆z = 2.5 mm and 4.0 mm, male F334 rats (n = 5) were scanned with a Bruker Avance III console interfaced with an Agilent 7T 16-cm bore magnet using the BBB-FEXI sequence. Imaging parameters were matched to simulations for b_f, t_m and b = 0, 250 s/mm²; TR = 5000 s; matrix size = 64 x 64; FOV = 32 x 32 mm²; single slice; repetitions = 10, with a spin-echo EPI readout. The signals were evaluated in Matlab R2021a using the standard AXR model [6, 7] and the full signal model [3], which accounts for effects of the crusher gradients, here coined the crusher-compensated exchange rate (CCXR) model: S = S'(t_m) exp(-((q_d²D + K)t_d)) x exp(-((q_m²D + K)t_m)) x exp(-((q_f²D + K)t_f)) f,
where q_f, q_m and q_d are the dephasing parameters associated with the filter block (f), mixing block (m) which incorporates the effect crusher gradients and detection block (d) (see Figure 1), D, K and f are matrices with intra-/extravascular diffusivities, forward/ backward exchange rates (k_in / k_out) and intra-/extra signal fraction respectively.
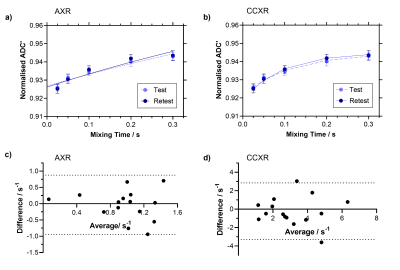
The intrasession repeatability was evaluated in F334 rats (n = 15) for both AXR and CCXR models at ∆z = 4 mm. The first five repetitions were used for test and the second five repetitions for retest. The coefficient of variation (CoV) is given by s_w/ µ x 100%.

RESULTS

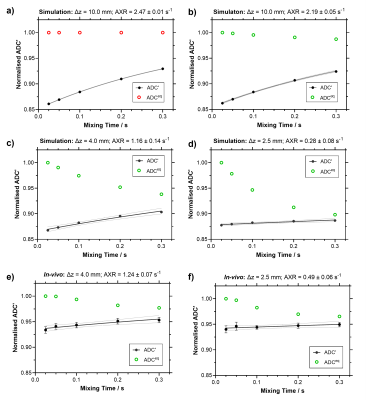
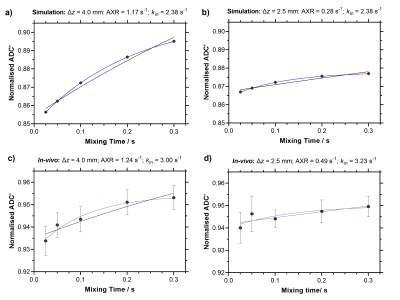
The simulations show that as slice thickness decreases, recovery of ADC’(t_m) becomes progressively attenuated leading to underestimation of AXR (2.19 s^-1, 1.16 s^-1 to 0.28 s^-1 for ∆z = 10.0 mm, 4.0 mm to 2.5 mm respectively), which is also reflected in the in vivo data where AXR = 1.24 ± 0.07 s^-1 and 0.49 ± 0.06 s^-1 at ∆z = 4.0 mm and 2.5 mm respectively (Figure 2). The CCXR model was able to recover the ground truth k_in value of 2.38 s^-1 for the signals simulated at both slice thicknesses at 4.0 mm and 2.5 mm, as expected (Figure 3a-b). In the in vivo protocol, the CCXR model gave mean k_in values of 3.00 s^-1 and 3.23 s^-1 for ∆z = 4.0 mm and 2.5 mm respectively (Figure 3c-d). The mean water exchange values (± standard deviation) for the repeatability study were AXR = 0.97 ± 0.32 s^-1 and k_in = 3.11 ± 1.08 s^-1 (Figure 4). Both models demonstrated reasonable repeatability with CoV of 33% and 35% for the AXR and CCXR models respectively.

DISCUSSION & CONCLUSION

Simulated and in vivo data show progressive underestimation of BBB water exchange measurements with decreasing slice thickness when using the AXR model. The CCXR model removes the biases induced by the crusher gradients, and provides measurements of water exchange in the rodent brain that are more consistent with the literature estimates (~2.5 s^-1 [4]). The CCXR model enables thinner slices in both the human and the rodent brain, which could be valuable for probing specific small brain regions particularly affected in diseases, such as the hippocampus in Alzheimer’s disease.

Acknowledgements

This work is funded by the EPSRC: grant code EP/S031510/1. SL has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No 804746).