3031

Free-water corrected Diffusion Kurtosis Imaging exhibits modified age-related trajectories of the measures in the brain white matter
Tomasz Pieciak1, Guillem París1, Dani Beck2,3,4, Ivan I. Maximov3,5, Antonio Tristán-Vega1, Rodrigo de Luis-García1, Lars T. Westlye2,3,6, and Santiago Aja-Fernández1
1ETSI Telecomunicación, Universidad de Valladolid, Valladolid, Spain, 2Department of Psychology, University of Oslo, Oslo, Norway, 3NORMENT, Division of Mental Health and Addiction, Oslo University Hospital & Institute of Clinical Medicine, University of Oslo, Oslo, Norway, 4Department of Psychiatric Research, Diakonhjemmet Hospital, Oslo, Norway, 5Department of Health and Functioning, Western Norway University of Applied Sciences, Bergen, Norway, 6KG Jebsen Centre for Neurodevelopmental Disorders, University of Oslo, Oslo, Norway

Synopsis

Keywords: White Matter, Diffusion/other diffusion imaging techniques

Diffusion kurtosis imaging (DKI) allows quantifying Gaussian and non-Gaussian effects in diffusion MRI signal and has already proved its relevance, including assessing age-related brain alterations. Hitherto, the standard DKI follows a single-component signal representation with no explicitly defined free-water factor that might lead to a reduced specificity of tensor-based measures. This work demonstrates the free-water corrections to the DKI and revisits the variations in the metrics across the adult lifespan. Our study shows a significant reduction in variability and dynamics of the kurtosis fractional anisotropy and the preservation of the status quo in the mean kurtosis tensor with age.

Introduction

The higher-order cumulant expansion of the diffusion MRI signal allows depicting of non-Gaussian effects of the signal1,2 intrinsically concealed within the standard Diffusion Tensor Imaging (DTI). Diffusion kurtosis imaging (DKI) is the common approach used to reveal such deviations from Gaussian diffusion2-5 with diverse clinical applications in the characterization of neural tissues6,7,8 and the evaluation of lifespan variations of the brain white matter (WM)9-12. However, the DKI signal representation is vulnerable to the partial volume effect caused by the free-water component13-15 that reflects the signal contribution from the cerebrospinal fluid and interstitial fluid in the extracellular space of the WM13. This work demonstrates the endeavours to correct the DKI-related measures for the free-water volume fraction (FWVF) and revisits the variations in kurtosis tensor-based measures across the adult lifespan.

Materials and methods

Sample population and data acquisition: The sample population included $$$ N = 287$$$ healthy subjects (178F/109M) aged 25-94 with no alcohol or drug addictions. The participants were scanned using a 3T General Electric Discovery MR750 scanner (GE, Waukesha, WI) using an EPI sequence with the parameters: TR=8150 ms, TE=83.1 ms, voxel size $$$2\times 2\times 2 \ \text{mm}^3$$$, $$$b\in\{1000,2000\} \ \text{s}/\text{mm}^2$$$ with $$$\{60,30\}$$$ uniformly distributed diffusion gradients respectively and 17 non-diffusion-weighted scans.

Data preprocessing: The diffusion MRI (dMRI) data underwent a standardized preprocessing pipeline16: noise removal17, Gibbs artifacts correction18, susceptibility-induced and eddy current distortions correction with the FSL topup tool (Analysis Group, FMRIB, Oxford, UK), followed by a quality assessment procedure19.

FWVF and DKI estimation: The FWVF parameter, $$$f$$$, was estimated from two-shell dMRI data using the spherical means approach14 and orientationally-averaged signals via the spherical harmonics decomposition at the order of $$$L=6$$$ and Laplace-Beltrami20 regularization with $$$\lambda=0.001$$$.

The FW-corrected DKI was modeled with the following two-component signal representation:$$ \frac{S(b,\mathbf{g})}{S(0)}=(1-f)\exp\left(-b \sum_{i,j=1}^3g_ig_jD_{ij}+\frac{b^2}{6}\left( \frac{1}{3}\sum_{i=1}^3 D_{ii}\right)^2\sum_{i,j,k,l=1}^3g_ig_jg_kg_lW_{ijkl}\right)+f\exp(-bD_f), $$
where $$$\mathbf{g}=[g_1,g_2,g_3]$$$ is the gradient direction, $$$D_{ij} $$$ are the second-order tensor entries, $$$W_{ijkl}$$$ are the fourth-order tensor (symmetric diffusion kurtosis tensor) elements, $$$D_f=3.0\times 10^{-3} \ \text{mm}^2/\text{s}$$$ is the apparent diffusion coefficient (a fixed value) of FW under a temperature of 37$$$^\circ$$$, and $$$f\in [0,1]$$$ is the pre-estimated FWVF.

The tensors were estimated via the weighted least squares (WLS) approach4 under two variants, namely a standard DKI with no FW assumption (i.e. $$$f=0$$$; hereafter referred to as the “Standard DKI”) and under a FW-corrected scenario with the observation vector $$ \mathbf{S} = \left[\frac{S(b,\mathbf{g}_1)-f\exp(-b_1 D_f)}{1-f}, \ldots, \frac{S(b,\mathbf{g}_n)-f\exp(-b_n D_f)}{1-f}\right]^T,$$
where $$$b_k$$$ is the b-value coupled with $$$\mathbf{g}_k$$$. We calculated two kurtosis tensor-based measures: kurtosis fractional anisotropy (KFA) and mean kurtosis tensor (MKT).

Data registration and regions of interest retrieval (ROIs): The DTI-based fractional anisotropy estimated at $$$b=1000 \ \text{s}/\text{mm}^2 $$$ via the WLS was non-linearly registered to the FSL template FMRIB58_FA. The ROIs were retrieved for each subject by inversely warping the labels from the JHU WM atlas21 to the subject’s native spaces.

Statistical analysis: The lifespan variations in DKI parameters are modeled using the quantile regression (QR) framework22,23 via the second-order polynomial as the function of the explanatory variable $$$Age$$$
$$Q(\tau|Age)=\beta_0+\beta_1Age+\beta_1Age^2 \ \ \ \text{with} \ \ \ \beta_l \in \mathbb{R}, $$ while the alterations in the DKI measures as a function of the FWVF $$$f$$$ are patterned with the first-order model$$ Q(\tau|f) = \beta_0 + \beta_1 f \ \ \ \text{with} \ \ \ \beta_l \in \mathbb{R} $$with $$$Q(\tau|\cdot)$$$ being the quantile function estimated under a fixed quantile $$$\tau$$$.

Results

  • Fig.1 visually inspects the FWVF and kurtosis tensor measures estimated under standard and FW-corrected variants. We observe a notable increase in the KFA under a FW-corrected scenario compared to the standard DKI.
  • Fig.2 presents the adult lifespan variations in the KFA/MKT. We recognize 1) increased (decreased) FW-corrected KFA (MKT) values, 2) reduced dynamics of the FW-corrected KFA compared to the standard equivalent, and 3) the preservation of the status quo in the MKT trend.
  • Fig.3 illustrates population density plots over seven age intervals, each contrasting the dynamics of standard versus FW-corrected KFA/MKT.
  • Fig.4 shows the measures as a function of the FWVF. We observe 1) the correlations between the FW-corrected KFA and the FWVF are weaker, 2) the slopes for the FW-corrected KFA under $$$\tau=0.5$$$ become non-significant in most cases.
  • Fig.5 shows the histograms of two kurtosis tensor components.

Discussion and conclusions

This paper studies the effect of the FW correction on the kurtosis tensor-based measures and its implications on the variations of the measures across the adult lifespan, leading to the following conclusions:
  1. The inclusion of the FWVF in the DKI estimation procedure reduced age-related variations reflected in decreased $$$R^1$$$ and inter-subject variabilities of the KFA (Fig.2), and population density plots (Fig.3). The dependency of the FW-corrected KFA on the FWVF has been significantly diminished, leading to non-significant correlations in the regions considered in the study (Fig.4). This suggests that the FWVF might be one of the factors causing the lifespan alterations in the KFA.
  2. The KFA exhibits a reduced heteroskedastic effect (i.e. the functional dependence of the variance with age; Fig.2). This effect is adequately modeled in the QR framework22,23, which does not assume the underlying statistical data properties.
  3. The MKT results suggest that the FWVF shifts the kurtosis tensor's trace negatively (Fig.4, Fig.5).

Acknowledgements

Tomasz Pieciak, Guillem París, Antonio Tristán-Vega, Rodrigo de Luis-García and Santiago Aja-Fernández acknowledge Ministerio de Ciencia e Innovación Gobierno de España with research grants PID2021-124407NB-I00 and TED2021-130758B-I00. Tomasz Pieciak acknowledges the Polish National Agency for Academic Exchange for grant PPN/BEK/2019/1/00421 under the Bekker programme and the Ministry of Science and Higher Education (Poland) under the scholarship for outstanding young scientists (692/STYP/13/2018). Guillem París was funded by the Consejería de Educación de Castilla y León and the European Social Fund through the “Ayudas para financiar la contratación predoctoral de personal investigador - Orden EDU/1100/2017 12/12” program. The study is supported by the Research Council of Norway (223273, 249795, 298646, 300767), the South-Eastern Norway Regional Health Authority (2014097, 2019101), the Norwegian ExtraFoundation for Health and Rehabilitation (2015/FO5146), KG Jebsen Stiftelsen, and the European Research Council under the European Union's Horizon 2020 research and Innovation program (ERC 802998).

References

  1. Afzali, M., Pieciak, T., Jones, D. K., Schneider, J. E., Ozarslan, E. (2022). Cumulant Expansion with Localization: A new representation of the diffusion MRI signal. Frontiers in Neuroimaging. https://doi.org/10.3389/fnimg.2022.958680
  2. Poot, D. H., Arnold, J., Achten, E., Verhoye, M., Sijbers, J. (2010). Optimal experimental design for diffusion kurtosis imaging. IEEE transactions on medical imaging, 29(3), 819-829.
  3. Jensen, J. H., Helpern, J. A., Ramani, A., Lu, H., Kaczynski, K. (2005). Diffusional kurtosis imaging: the quantification of non‐gaussian water diffusion by means of magnetic resonance imaging. Magnetic Resonance in Medicine, 53(6), 1432-1440.
  4. Veraart, J., Poot, D. H., Van Hecke, W., Blockx, I., Van der Linden, A., Verhoye, M., Sijbers, J. (2011). More accurate estimation of diffusion tensor parameters using diffusion kurtosis imaging. Magnetic resonance in medicine, 65(1), 138-145.
  5. Henriques, R. N., Correia, M. M., Nunes, R. G., Ferreira, H. A. (2015). Exploring the 3D geometry of the diffusion kurtosis tensor—Impact on the development of robust tractography procedures and novel biomarkers. Neuroimage, 111, 85-99.
  6. Wu, E. X., Cheung, M. M. (2010). MR diffusion kurtosis imaging for neural tissue characterization. NMR in Biomedicine, 23(7), 836-848.
  7. Van Cauter, S., Veraart, J., Sijbers, J., Peeters, R. R., Himmelreich, U., De Keyzer, F., Van Gool, S. W., Van Calenbergh, F., Van Hecke, W., Sunaert, S. (2012). Gliomas: diffusion kurtosis MR imaging in grading. Radiology, 263(2), 492-501.
  8. Wang, J. J., Lin, W. Y., Lu, C. S., Weng, Y. H., Ng, S. H., Wang, C. H., Liu, H. L., Hsieh, R. H., Wan, Y.L., Wai, Y. Y. (2011). Parkinson disease: diagnostic utility of diffusion kurtosis imaging. Radiology, 261(1), 210-217.
  9. Beck, D., de Lange, A. M. G., Maximov, I. I., Richard, G., Andreassen, O. A., Nordvik, J. E., Westlye, L. T. (2021). White matter microstructure across the adult lifespan: A mixed longitudinal and cross-sectional study using advanced diffusion models and brain-age prediction. NeuroImage, 224, 117441.
  10. Coutu, J. P., Chen, J. J., Rosas, H. D., Salat, D. H. (2014). Non-Gaussian water diffusion in aging white matter. Neurobiology of aging, 35(6), 1412-1421.
  11. Benitez, A., Jensen, J. H., Falangola, M. F., Nietert, P. J., Helpern, J. A. (2018). Modeling white matter tract integrity in aging with diffusional kurtosis imaging. Neurobiology of aging, 70, 265-275.
  12. Taha, H. T., Chad, J. A., Chen, J. J. (2022). DKI enhances the sensitivity and interpretability of age-related DTI patterns in the white matter of UK biobank participants. Neurobiology of Aging, 115, 39-49.
  13. Pasternak, O., Sochen, N., Gur, Y., Intrator, N., Assaf, Y. (2009). Free water elimination and mapping from diffusion MRI. Magnetic Resonance in Medicine, 62(3), 717-730.
  14. Tristán‐Vega, A., París, G., de Luis‐García, R., Aja‐Fernández, S. (2022). Accurate free‐water estimation in white matter from fast diffusion MRI acquisitions using the spherical means technique. Magnetic Resonance in Medicine, 87(2), 1028-1035.
  15. Pieciak, T., París, G., Beck, D., Maximov, I., Tristán-Vega, A., de Luis-García, R., Westlye, L.T., Aja-Fernández, S. (2022). Free-water volume fraction increases non-linearly with age in the white matter of the healthy human brain. https://www.biorxiv.org/content/10.1101/2022.10.06.510800v1.abstract
  16. Maximov, I. I., Alnæs, D., Westlye, L. T. (2019). Towards an optimised processing pipeline for diffusion magnetic resonance imaging data: Effects of artefact corrections on diffusion metrics and their age associations in UK Biobank. Human Brain Mapping, 40(14), 4146-4162.
  17. Veraart, J., Novikov, D. S., Christiaens, D., Ades-Aron, B., Sijbers, J., Fieremans, E. (2016). Denoising of diffusion MRI using random matrix theory. Neuroimage, 142, 394-406.
  18. Kellner, E., Dhital, B., Kiselev, V. G., Reisert, M. (2016). Gibbs‐ringing artifact removal based on local subvoxel‐shifts. Magnetic resonance in medicine, 76(5), 1574-1581.
  19. Roalf, D. R., Quarmley, M., Elliott, M. A., Satterthwaite, T. D., Vandekar, S. N., Ruparel, K., et al. (2016). The impact of quality assurance assessment on diffusion tensor imaging outcomes in a large-scale population-based cohort. Neuroimage, 125, 903-919.
  20. Descoteaux, M., Angelino, E., Fitzgibbons, S., Deriche, R. (2007). Regularized, fast, and robust analytical Q‐ball imaging. Magnetic Resonance in Medicine, 58(3), 497-510.
  21. Mori, S., Wakana, S., Van Zijl, P. C., Nagae-Poetscher, L. M. (2005). MRI atlas of human white matter. Elsevier.
  22. Koenker, R., Hallock, K. F. (2001). Quantile regression. Journal of economic perspectives, 15(4), 143-156.
  23. Koenker, R., Machado, J. A. (1999). Goodness of fit and related inference processes for quantile regression. Journal of the american statistical association, 94(448), 1296-1310.
  24. Doane, D. P. (1976). Aesthetic frequency classifications. The American Statistician, 30(4), 181-183.

Figures

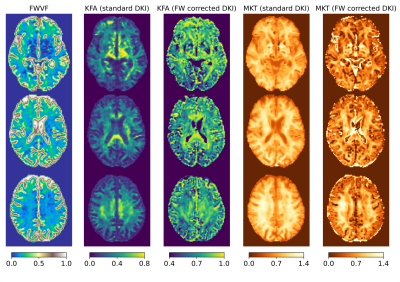
Figure 1. Visual inspection of the measures for a single subject aged 69 presented in three axial slices. From the left: free-water volume fraction (FWVF) and two DKI measures: kurtosis fractional anisotropy (KFA) and mean kurtosis tensor (MKT). The DKI measures were estimated under two variants: a standard single-component DKI representation and a FW-corrected DKI (i.e., two-component representation). Notice that the FW-corrected KFA measure is shown under a different dynamic range than the standard DKI counterpart.

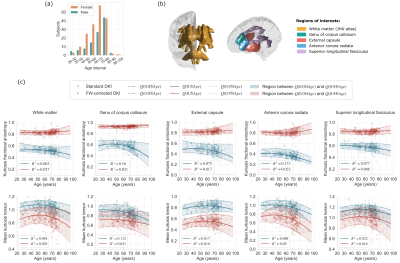
Figure 2. (a) Population sample, (b) regions of interest (ROIs), and (c) the trajectories of kurtosis tensor parameters across the adult lifespan. Each marker presents a median value of the measure over the ROI in the subject's native space. The solid lines show the quantile function $$$Q(0.5|Age)$$$ (median), the lower dotted lines indicate $$$Q(0.05|Age)$$$ (5th percentile), and the upper dashed lines present $$$Q(0.95|Age)$$$ (95th percentile), all three computed from median values over the ROI. The parameter $$$R^1(\tau=0.5)$$$ refers to the goodness-of-fit of the model.

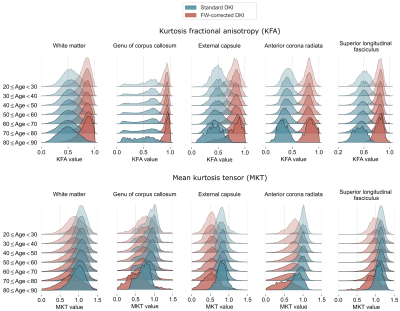
Figure 3. Population distributions of the DKI measures were estimated under the single-component representation (i.e. standard DKI) and an FW-corrected scenario. An individual ROI is illustrated by density plots computed over seven age intervals, aggregating the values from the native subjects' spaces. Doane's method24 was employed to estimate the optimal bins per density plot.

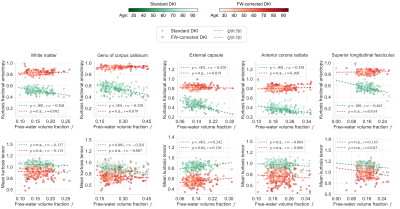
Figure 4. The DKI measures under both variants (i.e., standard representation and FW-corrected) are plotted as a function of FWVF, $$$ f $$$. The subject's age has been encoded with the brightness of the marker and follows the notation included in the colorbars. Dashed lines present the quantile function $$$Q(0.5|f)$$$, $$$p$$$-values refer to the significance of the slopes with the abbreviation “n.s.” specifying not statistically significant slopes at the alpha level of 0.05 and $$$r$$$ denotes the Pearson's correlation coefficient of the model fitted under $$$ \tau = 0.5$$$.


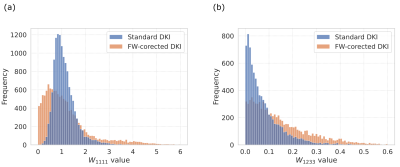
Figure 5. Histograms presenting the kurtosis tensor elements of the subject from Fig. 1: (a) $$$W_{1111}$$$ (kurtosis tensor trace element; used to calculate the MKT) and (b) $$$W_{1233}$$$. Each histogram aggregates the elements of the kurtosis tensor estimated under a standard DKI and FW-corrected DKI.

Proc. Intl. Soc. Mag. Reson. Med. 31 (2023)
3031
DOI: https://doi.org/10.58530/2023/3031