2991

In silico optimization of iopamidol CEST MRI for renal pH mapping at 3 Tesla

Julia Stabinska^1,2, Moritz Zaiss^3,4, Adnan Bibic¹, Farzad Sedaghat², Cristina L Sadowsky^5,6, Peter CM van Zijl^1,2, and Michael T McMahon^1,2
¹F.M. Kirby Research Center for Functional Brain Imaging, Kennedy Krieger Institute, Baltimore, MD, United States, ²The Russell H. Morgan Department of Radiology and Radiological Science, The Johns Hopkins University School of Medicine, Baltimore, MD, United States, ³High-field Magnetic Resonance Center, Max Planck Institute for Biological Cybernetics, Tuebingen, Germany, ⁴Institute of Neuroradiology, Friedrich-Alexander University Erlangen-Nürnberg (FAU), Erlangen, Germany, ⁵International Center for Spinal Cord Injury, Kennedy Krieger Institute, Baltimore, MD, United States, ⁶Physical Medicine and Rehabilitation, The Johns Hopkins University School of Medicine, Baltimore, MD, United States

Synopsis

Keywords: CEST & MT, CEST & MT

In vivo optimization of CEST iopamidol contrast in human subjects is complicated and requires multiple examinations and injections of the agent. To address this challenge, we propose application of a numerical approach that utilizes exchange rates determined under physiological conditions at 17.6T to perform kidney-like multi-pool Bloch-McConnell simulations for in silico optimization of saturation parameters for 3T applications. Our results suggest that the iopamidol-based CEST MRI is sensitive to pH in the range between 6 and 7.2 with the optimal results when short CEST saturation pulses (3x100 ms), low B1 strength (B₁~0.8 µT) and short recovery time (T_rec~T_1w) are applied.

Introduction

As the kidneys play a predominant role in maintaining internal acid-base homeostasis, pH may be a useful biomarker of renal function. With its high sensitivity to pH, iopamidol-enhanced chemical exchange saturation transfer (CEST) MRI is potentially an attractive tool for the in vivo detection of kidney disease. Despite encouraging results from several preclinical studies^1–3, the feasibility of CEST-based renal pH mapping at clinical field strengths has not been fully determined. A main reason is the complexity of CEST contrast optimization in human subjects, which typically requires multiple MRI scanning sessions and injections of contrast agent. The objective of this study was to address this limitation by applying a recently proposed numerical approach⁴. First, exchange rates of iopamidol protons at physiological conditions were quantified and used to create a kidney-like system with realistic water relaxation rates at 3T and a semi-solid magnetization transfer (ssMT) component. In the next step, this numerical multi-pool model was employed in Bloch-McConnell simulations to investigate changes in CEST signal and saturation transfer ratio depending on the presaturation parameters allowing to find the optimal parameters for renal pH mapping on 3T scanners.

Methods

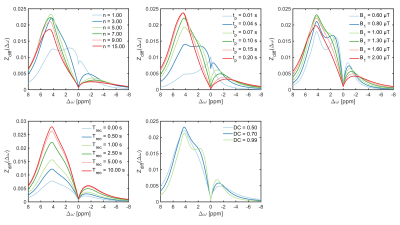
Six solutions of 25 mM iopamidol dissolved in phosphate-buffered saline at different pH values between 5.8 and 7.4 were prepared and examined on a 17.6 T spectrometer. The temperature of the samples was kept constant at 37°C. For CEST measurements, a rectangular pulse of 7.2 s at five different saturation field strengths (B1) between 2.4 and 4.8 µT was used. Z-spectra were sampled at 201 frequency offsets between ±10 ppm.
Data analysis, simulations und Bloch-McConnell fitting were performed in Matlab⁵. The simulation files are available on github (https://github.com/cest‐sources/BM_sim_fit). All 30 Z-spectra were fitted simultaneously using a multi-pH-multi-B₁ method by extending the Bloch equations to use pH as a parameter, and assuming that the change in exchange rate can be expressed as a sum of changes in base- and water-catalyzed exchange (k_x=k_x1·10^pH-7+k_x0), as the buffer contribution remains constant. Subsequently, using the estimated exchange rates and kidney tissue properties at 3T^6,7, a kidney-like model including a water pool, ssMT pool and four iopamidol proton pools (see Figure 1 for assignment) was created to optimize the saturation parameters. Iopamidol contrast (Z_diff) was calculated by subtracting the Z-spectra with (Z_post:6 pool) from those without (Z_pre:2 pool) the iopamidol pools activated. In the next step, the saturation transfer ratio ST_ratio=Z_diff (4.3 ppm)/Z_diff (5.5 ppm) was determined for different combinations of B₁ and number of saturation pulses (n) of length (tp) of 0.1 s (i.e varying the total saturation time).

Results

The results of the multi-pH-multi-B₁ fitting at 17.6 T are displayed in Figure 1, which reveals that the exchange rates of amide protons at 5.5 and 4.3 ppm increased from 106±9 s^-1 to 3796±83 s^-1 and 34±4 s^-1 to 1199±37 s^-1, respectively, in the pH range from 5.8 to 7.4.
Figure 2 shows exemplary results of the CEST parameter optimization process with respect to iopamidol contrast at an average pH of 6.7⁸. At this pH value, the optimal parameters yielding ~2.5% CEST effect at 4.3 ppm and ~1.5% at 5.5 ppm were: n=3, t_p=0.1 s, B₁=1.0 µT, T_rec=2.5 s and DC=0.5.
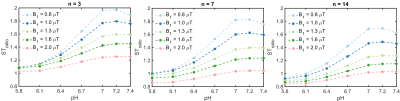
The ratiometric CEST signals calculated for different combinations of n and B₁ values are displayed in Figure 3. These results suggest that the ratiometric CEST analysis allows measurements of pH in the range between 6 and 7.0 with the highest sensitivity obtained for n=3 and B₁=0.8 µT.

Discussion

In this study, we determined iopamidol exchange rates under physiological conditions at 17.6T, and used these to create a kidney-like system including realistic water relaxation times and ssMT component at 3T. This model was then employed in Bloch McConnell simulations with different saturation parameters to establish optimal saturation conditions for in vivo renal pH mapping at 3T.
The exchange rates estimated here are slightly higher than those obtained at room temperature in a previous study⁹, which is consistent with faster exchange at higher temperatures. Still, with highest exchange rate of about 4000 s^-1 at pH 7.4 and relatively large chemicals shifts of the amide groups at 4.3 and 5.5 ppm, iopamidol appears to be an attractive CEST agent for clinical applications at 3T. The optimal CEST parameters found in our study suggest that sufficient saturation of both amide groups and high sensitivity to pH in the physiological range can be achieved using short RF pulses (3x100 ms) with low B₁~0.8 µT, and short T_rec=2.5 s. This combination is particularly favorable for contrast-enhanced CEST acquisitions, which are limited by rapid renal clearance of iopamidol that determines temporal resolution.
The numerical approach applied in our study can be used as guidance for in vivo optimization in human subjects without the need for multiple injections of contrast agent during a single examination. Nevertheless, the optimal parameters predicted by our simulations should be verified experimentally.

Conclusion

Using iopamidol exchange rates determined in the physiological pH range and temperature, the sensitivity of pH imaging was found to be optimal when short saturation time and a relatively low B₁ was applied. The numerical approach used here can aid the optimization of iopamidol CEST MRI without the need for injections.

Acknowledgements

This work is supported by NIH grant 5R01DK121847-02 and by a Kennedy Krieger Institute Goldstein Innovation and Collaboration Award.

References

1. Longo DL, Busato A, Lanzardo S, Antico F, Aime S. Imaging the pH evolution of an acute kidney injury model by means of iopamidol, a MRI-CEST pH-responsive contrast agent. Magnetic Resonance in Medicine. 2013;70(3):859-864

2. Longo DL, Cutrin JC, Michelotti F, Irrera P, Aime S. Noninvasive evaluation of renal pH homeostasis after ischemia reperfusion injury by CEST-MRI. NMR in Biomedicine. 2017;30(7):e3720.

3. Stabinska J, Singh A, Haney NM, et al. Noninvasive assessment of renal dynamics and pH in a unilateral ureter obstruction model using DCE MR-CEST urography. Magnetic Resonance in Medicine. n/a(n/a).

4. Zaiss M, Anemone A, Goerke S, et al. Quantification of hydroxyl exchange of D-Glucose at physiological conditions for optimization of glucoCEST MRI at 3, 7 and 9.4 Tesla. NMR in Biomedicine. 2019;32(9):e4113.

5. Zaiss M, Angelovski G, Demetriou E, McMahon MT, Golay X, Scheffler K. QUESP and QUEST revisited – fast and accurate quantitative CEST experiments. Magnetic Resonance in Medicine. 2018;79(3):1708-1721.

6. Stanisz GJ, Odrobina EE, Pun J, et al. T1, T2 relaxation and magnetization transfer in tissue at 3T. Magnetic Resonance in Medicine. 2005;54(3):507-512.

7. Jiang K, Ferguson CM, Grimm RC, Zhu X, Glockner JF, Lerman LO. Reliable Assessment of Swine Renal Fibrosis Using Quantitative Magnetization Transfer Imaging. Investigative Radiology. 2022;57(5):334-342.

8. Brenner BM, Levine, Samuel A. Brenner and Rector’s the Kidney. Vol 2. 8th ed. Saunders Elsevier; 2008.

9. Sun PZ, Longo DL, Hu W, Xiao G, Wu R. Quantification of iopamidol multi-site chemical exchange properties for ratiometric chemical exchange saturation transfer (CEST) imaging of pH. Phys Med Biol. 2014;59(16):4493-4504.

Figures

Figure 1: (A) Z-spectra data points (dark tone) collected in iopamidol model solutions at pH 6.1 and 7.0 at 17.6 T, and corresponding fitted Z-spectra (light tone) obtained by simultaneous multi-pH-multi-B₁ fitting with the exchange rates and relaxation rates of water as free fit parameters. (B) pH-dependent exchange rates of iopamidol protons at 37°C.

Figure 2: In silico optimization of iopamidol contrast (Z_diff) in a kidney tissue-like model with realistic water relaxation times (T₁=2.03 s, T₂=50 ms) and ssMT pool (f_c=0.05, T_2c=10.5 µs) at 3T. Z_diff spectra obtained for different sets of CEST parameters, including varying number of saturation pulses (n), pulse duration (t_p), RF field strength (B₁), recovery time (T_rec) and duty cycle (DC).

Figure 3: In silico optimization of ratiometric CEST signal (ST_ratio) of iopamidol in the physiological pH range. Each subplot shows results obtained at different saturation strength (B₁ = 0.8, 1.0, 1.3, 1.6 and 2.0 µT), and number of saturation pulses (n = 3, 7 and 14). Pulse duration (t_p = 0.1 s), recovery time (T_rec = 2.5 s) and duty cycle (DC = 0.5) were constant.

Proc. Intl. Soc. Mag. Reson. Med. 31 (2023)

2991

DOI: https://doi.org/10.58530/2023/2991