Synopsis

Keywords: Data Processing, Data Processing

We estimated biophysical model parameters using a dictionary of diffusion signals. The dictionary is generated based on the set of biophysical model parameters. We then rotated this dictionary along fascicle direction derived from spherical deconvolution and tried to fit it to the diffusion signal using non-negative linear least square optimization to find the associated dictionary weights. These weights went through a deep learning network to find model parameters. Our approach shows reasonable accuracy and reliability for biophysical model estimation. It is also possible to extend our approach to more complex and general biophysical models to achieve higher specificity.

Introduction

Biophysical modeling of white matter (WM) has been used widely to determine tissue properties due to the specificity of these approaches. Many biophysical models are based on the Standard Model (SM), assuming multiple compartments to model diffusion signals. One drawback of this modeling approach is the degeneracy of the results as various sets of biophysical parameters can result in the same diffusion signal [1]. Some methods address this issue by constraining the solution. However, in some cases, these constraints are not biophysically justified and might introduce bias into the results. In this work, we propose a framework for estimating the properties of WM fascicles using machine learning in combination with a dictionary-based approach. We generate a dictionary of diffusion signals based on the model parameters within the biophysical acceptable range and fit it to the diffusion signal using non-negative linear least square (NNLS) optimization. We then train a neural network to predict the tissue parameters from the estimated weights. Here, we demonstrate the result of our approach on the synthetic and in-vivo data for the NODDI model.

Methods

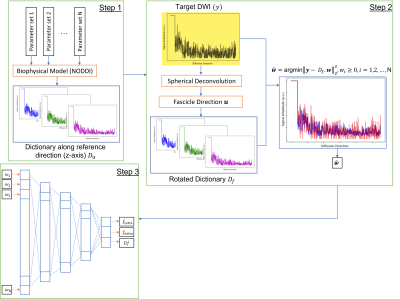
The diffusion signal can be described as the convolution of fiber orientation distribution function (fODF) $$$P({\bf n})$$$ and microstructural model $$$K(b,{\bf g.n})$$$:
$$S(b,{\bf g})=S_0\int_{S_2}P({\bf n}).K(b,{\bf g.n})d{\bf n}$$ Where $$$S(b,{\bf g})$$$ is the diffusion signal along gradient direction $$${\bf g}$$$ and b-value of $$$b$$$, and $$${\bf n}$$$ is fascicle direction. In a three-compartment setting, the kernel, $$$K$$$ can be defined as $$K(b,\xi)=f_{intra}e^{-bD_a \xi^2 }+f_{extra}e^{-bD_e^∥ \xi^2-bD_e^⊥ (1-\xi)^2}+f_{iso}e^{-bD_{iso}}$$ Where $$$\xi={\bf g.n}$$$ and [$$$f_{intra}, f_{extra}, D_a, D_e^∥, D_e^⊥, D_{iso} $$$] are the intra- and extra-axonal volume fraction, intra- and extra-axonal parallel and perpendicular diffusivities, and isotropic diffusivity, respectively. Figure 1 illustrates the basic idea of our approach for estimating the unknown model parameters.
We use these steps to generate diffusion signals based on the NODDI model: $$$f_{intra} \in[0,1]$$$, $$$f_{extra}\in[0,1-f_{intra}]$$$ with a step size of 0.2, $$$f_{iso}=1-f_{intra} -f_{extra} $$$, and $$$D_e^⊥\in[0.2,3] \mu m^2/ms$$$ with a step size of 0.5$$$\mu m^2/ms$$$. In our initial experiments, we assume a Watson distribution for the ODF and fix the fiber dispersion coefficient $$$\kappa$$$ to 20. The reference dictionary consists of N atoms $$$D_0=[{\bf d}_1^0,{\bf d}_2^0,…,{\bf d}_N^0 ]$$$ is generated for a multi-shell acquisition scheme corresponding to the MGH-HCP diffusion dataset with the following acquisition protocol: four shells of b-values of 1000, 3000, 5000, 10000 $$$\mu m^2/ms$$$, 64 directions for first two shells and 128 directions for other shells, TE of 57ms, and $$$\delta/\Delta$$$ (ms) of 12.9/21.8.
For every test data point, we extract the fiber direction using spherical deconvolution[4]. The reference dictionary is then rotated along that direction to create a new orientation-specific dictionary $$$D_f=[{\bf d}_1^f,{\bf d}_2^f,…,{\bf d}_N^f ]$$$. We then solve an NNLS optimization to find a set of dictionary atoms that fits the measured data: $${\bf \hat w}=argmin||{\bf y}-D_f.{\bf w}||_2^2,\space w_i≥0,\space i=1,2,…,N$$ Where $$${\bf w}$$$ is the weights corresponding to the atoms such that $$S=w_1 {\bf d}_1^f+w_2{\bf d}_2^f+⋯+w_N{\bf d}_N^f$$Since we are dealing with noisy data, multiple atoms with different weights would be resulted after solving the NNLS problem. To address this issue, we use DL network to compensate for the effect of noise while finding the biophysical parameters directly from the weights.
We generated one million datapoints with randomly chosen fascicle directions and model parameters and added Gaussian noise to reduce the SNR of data to 30. The data is divided by the ratio of 0.9 to train and test. All layers are fully connected. The NNLS weights are the input to the network and model parameters are the output. Activation function of each neuron is ReLu. Training is performed with batch size of 100 over 100 epochs while using Adam optimizer with learning rate of 1e-4.

Results

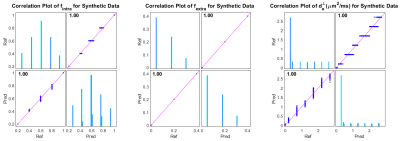
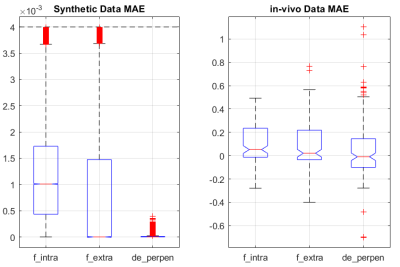
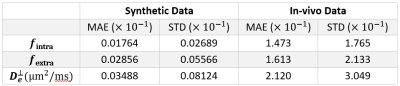
The mean absolute error (MAE) and standard deviation (STD), and boxplot of parameters error for synthetic and in-vivo data can be found in table 1, figure 3, and figure 4, respectively. To assess the performance of the proposed pipeline, we used the dMRI of a healthy female subject (25-29 years old) of the MGH-HCP dataset. 141 voxels within the Corpus Callosum (CC) are selected and fed to the Microstructure Diffusion Toolbox (MDT)[6] and the proposed pipeline. Figure 2 and 4 shows the predicted microstructural parameters and their comparison to the ground truth for synthetic and in-vivo data, respectively.

Discussion and Conclusion

In this work, we present preliminary results from a combined ML and dictionary-based approach for extracting biophysical parameters using standard diffusion MRI experiments. We showed that by employing this method, we can estimate properties of WM tissue in CC with reasonable accuracy. Our work is an extension of [7] which has shown the feasibility of extracting fascicle radii and density in a Monte Carlo setting, to the standard biophysical models. In future work, we can broaden this pipeline to include other biophysical models. Using DL network helps the denoising of data while making the computation of model parameters faster. This effect is more pronounced when we deal with greater number of atoms within the dictionary or more complex formation of fascicles. Overall, if adjusted for an arbitrary biophysical model, we expect our approach to be able to estimate model parameters with reasonable accuracy and reliability.

Acknowledgements

No acknowledgement found.

References

[1] Jelescu, I.O., Veraart, J., Fieremans, E., Novikov, D.S. “Degeneracy in model parameter estimation for multi-compartmental diffusion in neuronal tissue.” NMR Biomed. 29 (2016): 33–47.

[2] Zhang, Hui, et al. "NODDI: practical in vivo neurite orientation dispersion and density imaging of the human brain." Neuroimage 61.4 (2012): 1000-1016.

[3] Ma, D., Gulani, V., Seiberlich, N., Liu, K., Sunshine, J.L., Duerk, J.L. and Griswold, M.A. “Magnetic resonance fingerprinting.” Nature 495(7440) (2013): 187-192.

[4] Tournier, J.D., Calamante, F. and Connelly, A. “Robust determination of the fiber orientation distribution in diffusion MRI: non-negativity constrained super-resolved spherical deconvolution.” Neuroimage, 35(4) (2007): 1459-1472.

[5] Slawski, M. and Hein, M. “Sparse recovery by thresholded non-negative least squares.” In Advances in Neural Information Processing Systems (2011): 1926–1934.

[6] Harms, RL, et al. “Robust and fast nonlinear optimization of diffusion MRI microstructure models.” Neuroimage 155 (2017): 82-96.

[7] Rensonnet, G., Scherrer, B., Girard, G., Jankovski, A., Warfield, S.K., Macq, B., Thiran, J.P. and Taquet, M. “Towards microstructure fingerprinting: estimation of tissue properties from a dictionary of Monte Carlo diffusion MRI simulations.” NeuroImage, 184 (2019): 964-980.