Synopsis

Keywords: Image Reconstruction, Data Processing

Unsupervised deep learning framework that integrates system priors using unrolled optimization and general image priors can reconstruct high quality Magnetic Resonance images comparable to supervised methods from highly undersampled k-space data. We develop an unsupervised deep learning framework that integrates system priors in MR acquisition and image priors to reconstruct high quality MR images from highly undersampled k-space data without using ground truth images.

Purpose

To integrate general image priors in unsupervised deep learning frameworks for accelerated magnetic resonance imaging.

Introduction and Proposed Method

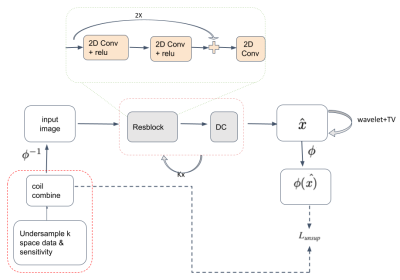
The data acquisition in accelerated Magnetic Resonance Imaging (MRI) [1] could be expressed as:$$y= \phi(x),\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(1)$$ where $$$y \in \mathbb{C}^{1X M}$$$ is the vectorized undersampled k-space measurement, $$$\phi$$$ is forward operator representing partial Fourier operation and coil sensitivities, and vectorization, $$$x \in \mathbb{C}^{1 X N}$$$ is the unobserved, desired image. Since $$$M << N$$$, the system of the equations is ill-posed. To solve this ill-posed problem and reconstruct $$$x$$$ from $$$y$$$, the classical reconstruction frameworks pose it as a constrained optimization problem such that:
$$ x^{*} = arg min_x ||y-\phi(x)||^2+\lambda\mathcal{R} (x), \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(2)$$ where $$$||y-\phi(x)||^2$$$ ensures data consistency with measured data and $$$\mathcal{R}(.)$$$ is a regularization term which enforces image priors. Some classical image priors are smoothness in total variation (TV) [2], sparsity in wavelet representation [3], and low rankness [4]. In a supervised deep learning (DL) framework, the image priors are learned using convolutional neural networks (CNN) [5] such that $$$\mathcal{R} (x) \rightarrow \mathcal{R}_{CNN}(x)$$$ by minimizing some loss function $$$\mathcal{L}(\widehat{x}, x)$$$ for a given a training data set $$$x^u_i, x_i$$$, $$$i = 1, 2, 3, \cdots T$$$ of image pairs; aliased undersampled image $$$x^u$$$ and fully sampled desired images $$$x$$$. Some examples of popular loss function $$$\mathcal{L}(\cdot)$$$ in the supervised framework are $$$l_1$$$ norm, $$$l_2$$$ norm, and mean squared error. For example, the supervised deep learning model approach can be represented as $$arg min_{x,\theta} ||y-\phi(x)||^2 + \lambda ||x-f_{\theta}(x_u|\theta) ||_2^2, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(3)$$
where $$$f_{\theta}$$$ is the forward network parameterized by $$$\theta$$$, which takes an undersampled image and produces an estimation $$$ \widehat(x)$$$ of fully sampled desired image $$$x$$$, such that $$$\widehat{x}$$$ = $$$f_{\theta}(x_u|\theta) $$$. The first term in equation 3 enforces the data consistency and acquisition system priors such as coil sensitivities and acquisition model [6]. Such frameworks are termed the "Unrolled Deep Learning" model [5][7]. However, in many cases, the fully sampled images $$$x$$$ are not available so the second term of equation 3 can not be computed. The parameters $$$\theta$$$ learned by such unsupervised deep learning frameworks are not regularized and the image reconstructed is not efficient. In [8] Generative adversarial models are used for unsupervised MR reconstruction by using data consistency to regulate the parameters of the Generative block. However, such constraints to regulate network parameters are not strong and can lead to the wrong reconstruction. In [9] authors use image priors to regulate deep learning parameters in an unsupervised fashion for image denoising and single-channel accelerated reconstruction. To exploit the benefits of both unrolled optimization that enforces system priors such as multi-coil images, and sensitivity maps, and the benefits of general image priors such as TV, wavelet, and low-rankness, we build a combined Unsupervised DL framework that integrates the unrolled optimization and image priors as shown in Fig. 1. For our unsupervised model, the reference image is not provided, so we formulated the loss in our model as $$ L_{unsup} = ||y-\phi(f_{\theta}(x_u|\theta))||_2^2 + \lambda \mathcal{R} (f_{\theta}(x_u|\theta)).\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(4)$$ We use $$$\mathcal{R}(\cdot)$$$ to be $$$l_1$$$ norm of Wavelet and Total variation transformation of $$$\widehat{x} $$$.

Experiments and Results

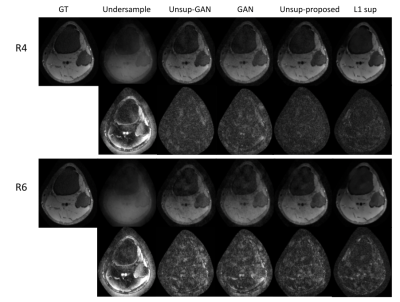
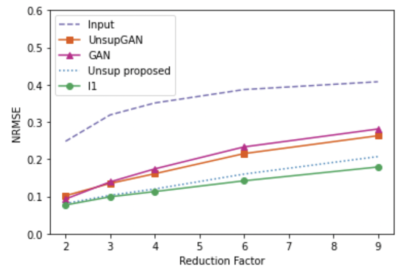
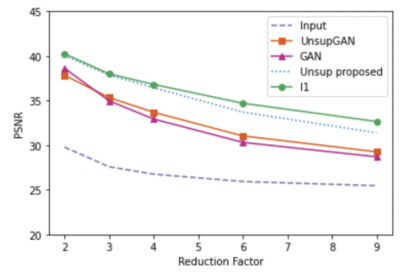
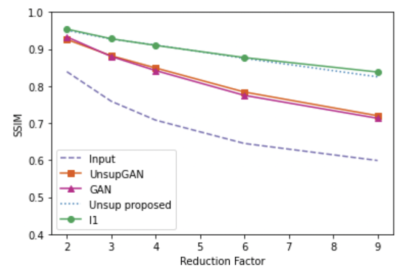
We used fully sampled 3T knee images from [10]. Each subject (data) is a complex-valued volume of size $$$320 X320 X 256 $$$ knee images. The volume images were split into axial slices of size $$$320 X 256 $$$. We use BART [11] to generate pseudo-random Poisson-disc masks to generate undersampled k-space data as input. Coil sensitivity maps are generated using the SENSE [6] method. During training, the training data consisted only of multi-coiled undersampled k-space data at an undersampling rate of 2, 3, 4, 6, 8, and 9. A total of 4800 undersampled data was used during training. No fully sampled images were used in the proposed method and Unsupersied GAN method training. Test data sets with an undersampling factor of 2, 3, 4, 6, 8, and 9 were also created. Each test set consisted of 1100 undersampled k-space data with corresponding undersampling rates. In addition to our method, we have conducted experiments on contemporary methods, such as supervised GAN, Unsupervised GAN [8], and supervised unrolled CNN using l1 loss [7]. Figure 2 shows the representative reconstructed images for reduction factors 4 and 6. From the figure, we can see the proposed unsupervised method has a better performance than all other methods except for the supervised l1 method. The proposed unsupervised method still has comparable results to the supervised l1 method, if not better. Figures 3, 4, and 5 present compare quantitative error and performance metrics NRMSE, PSNR, and SSIM respectively for all test data set and all reduction factor. The quantitative results also show that the proposed unsupervised method performs better than all other contemporary methods and has comparable results to the supervised unrolled l1 method which requires ground truth images for training.

Conclusion

We proposed an unsupervised deep learning framework for accelerated magnetic resonance imaging. Our proposed technique integrates system priors and classical image priors to train DL frameworks for accelerated MRI without the ground truth. The proposed method has better performance than all contemporary supervised models and has comparable results to unrolled supervised model.

Acknowledgements

No acknowledgement found.