2935
Deep Learning-based MRI Reconstruction with Artificial Fourier Transform(AFT)-Net
Yanting Yang1, Andrew F. Laine1, and Jia Guo2,3
1Department of Biomedical Engineering, Columbia University, New York, NY, United States, 2Department of Psychiatry, Columbia University, New York, NY, United States, 3Mortimer B. Zuckerman Mind Brain Behavior Institute, Columbia University, New York, NY, United States
1Department of Biomedical Engineering, Columbia University, New York, NY, United States, 2Department of Psychiatry, Columbia University, New York, NY, United States, 3Mortimer B. Zuckerman Mind Brain Behavior Institute, Columbia University, New York, NY, United States
Synopsis
Keywords: Image Reconstruction, Machine Learning/Artificial Intelligence
Conventional medical image reconstruction methods are less parametric and lack generality due to random error and noise. A novel artificial Fourier transform (AFT) framework is developed which determines the mapping between k-space and i-space like DFT while can be fine-tuned with further training. The flexibility of AFT allows it to be simply incorporated into any existing deep learning network as learnable or static blocks. Reconstruction and denoising tasks are combined into a unified network that simultaneously enhances the image quality. AFT-Net achieves competitive results compared with other methods and proofs to be more robust to additional noise and contrast differences.Introduction
Medical image reconstruction from the sensor domain to the image domain is critical because it lays the foundation for the following image analysis tasks. How we reconstruct and process the raw data acquired from the imaging system sensors directly influences the overall image quality. To solve the problem mentioned above, a unified complex-valued image reconstruction approach is proposed for magnetic resonance images (MRI). The framework described in this study is the artificial Fourier transformation (AFT) which has the full functionality of the state-of-the-art Fourier transform and can be fine-tuned through further training. AFT can be incorporated into any existing deep learning pipeline with fully adjustable parameters. We utilize AFT combined with deep complex-valued networks to design the AFT-Net for MRI reconstruction plus denoising and reconstruction plus accelerated imaging.Material and Methods
2.1 DatasetsThe models are trained on a real-world dataset that contains mouse brain T2w MRI scans over 243 subjects. Each subject is scanned for 4 repetitions, and the size of each slice is $$$201\times402$$$ with resolution $$$0.075mm\times0.075mm$$$. The trained networks are further evaluated on MRI scans with other modalities and different contrast on 10 subjects randomly selected from the testing set. For the dataset with simulated additional Gaussian noise in k-space, we add random Gaussian noise to the real and the imaginary part of k-space data separately. For the dataset with different contrast caused by GBCA, we use the T2-weighted contrast-enhanced MRI scanned from the same 10 subjects.
2.2 Network Architecture
The general workflow and the network structure are shown in Figure 1. We implement complex-valued neural networks and propose AFT with two successive blocks. Each block consists of two complex linear layers followed by a transpose operation. To combine reconstruction with other tasks, we incorporate our AFT with a complex-valued U-Net1 which extracts higher features in the k-space or i-space domain and forces the network to represent sparsely in that domain.
Results
3.1 ReconstructionWe train our AFT on the real-world T2-weighted 4-coils k-space raw data and compare it with the comparative method AUTOMAP2. The residual map between the ground truth and AFT prediction is presented in Figure 2a. It can be seen that no mouse brain structural information is shown in the residual, so the error is mainly caused by precision loss during floating-point calculation in matrix multiplication. The maximum error exists in the eyes and neck region, where motion artifacts are commonly present due to respiration and eye movement, which is inevitable for in-vivo MRI scans.
3.2 Reconstruction plus denoising
The AFT-Net trained on the real-world dataset aims to combine reconstruction and denoising. The models are compared with the numerical method, real-valued neural networks, DFT-based networks, and other methods. Given k-space data containing noise, AFT-Net can learn the mapping between two domains, remove noise and preserve useful structural information as shown in Figure 3. The proposed AFT outperforms AUTOMAP even without implementing non-linear activation functions and CNNs. Comparing AFT with AFT_CUNet, CNNs extract higher features and introduce non-linearity, enhancing overall performance. Comparing DFT_CUNet with AFT_CUNet, the AFT can remove noise artifacts in k-space before feeding into CNNs while keeping the anatomy information needed. Comparing AFT_UNet with AFT_CUNet, the complex-valued network leverages the correlation between the real and imaginary parts and is superior to the real-valued counterpart. The real-valued network performs worse in terms of PSNR and SSIM due to failed elimination of some abnormal values in the image domain.
3.3 Evaluation on the datasets with artifacts
The trained networks are evaluated on the T1w MRI with additional Gaussian noise and T2w MTI with GBCAs. The networks trained on the real-world dataset are used as pre-trained models and retrained on the T1w MRI. The results are shown in Figure 4. Our AFT-Net can keep the structure of vessels while removing noise. The AFT-Net is also more robust to the contrast difference presented in the image domain and shows an overall improvement compared with AUTOMAP. AFT-Net can be easily applied to medical image reconstruction and denoising with other modalities using transfer learning.
3.4 Reconstruction plus accelerated imaging
We also verify that reconstruction can be combined with the accelerated imaging task which can not be easily achieved in i-space. K-space data from the real-world T2w MRI dataset are undersampled in the phase-encoding direction by 2 times3 and the results are shown in Figure 5. Our AFT-Net achieves significant improvement and increases the input PSNR by 10dB, which indicates the generality and wide potential application of AFT-Net.
Discussion and Conclusion
Figure 2, 3, 4, and 5 demonstrate that AFT-Net achieves competitive results compared with other methods and proofs to be more robust to additional noise and contrast differences. An extensive study on the transfer learning on the dataset with different contrast caused by different scan modalities demonstrates the strength and generality of our approach.One remaining limitation is that we only implement a complex-valued network with linear layers and CNNs, which are less effective than some advanced architectures. In our future work, we will aim to replace multi-layer perceptron and CNNs with transformer-based and diffusion-based models while extending the concept of AFT to more medical imaging tasks from 2D imaging processing to 1D spectroscopy analysis.
Acknowledgements
This study was performed at the Zuckerman Mind Brain Behavior Institute at Columbia University and Columbia MR Research Center site.References
1. X Wu, D Sikka, N Igra, S Gjerwold-Sellec, C Gao, and JGuo. Cu-net: A completely complex u-net for mr k-space signal processing. In Proceedings of International Society of Magnetic Resonance in Medicine, 2021.
2. Bo Zhu, Jeremiah Z Liu, Stephen F Cauley, Bruce R Rosen, and Matthew S Rosen. Image reconstruction by domain-transform manifold learning. Nature, 555(7697):487–492,201.
3. Anagha Deshmane, Vikas Gulani, Mark A Griswold, andNicole Seiberlich. Parallel mr imaging. Journal of MagneticResonance Imaging, 36(1):55–72, 20
Figures
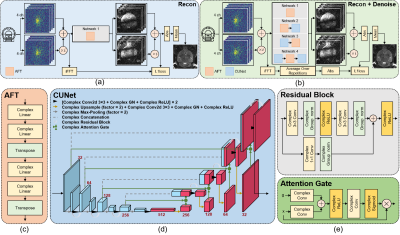
Figure 1: Overview of the AFT-Net framework. (a) Workflow for reconstruction task. In the reconstruction task, the target is derived by taking iFFT over the raw k-space data and only AFT is evaluated in this task. (b) Workflow for reconstruction plus denoising task. In the reconstruction plus denoising task, the target is derived by taking the average over repetitions after iFFT. (c) Structural of AFT. (d) Structural of CUNet. (e) Structural of residual block and attention gate block.
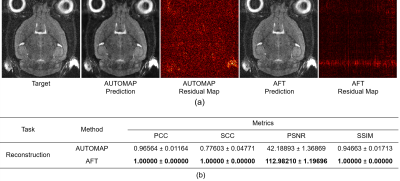
Figure 2: Qualitative comparison and quantitative comparison of different reconstruction methods. (a) Reconstruction results and residual maps on the real-world T2w MRI dataset. (b) Table of metrics for different reconstruction methods in terms of PCC, SCC, PSNR, and SSIM.
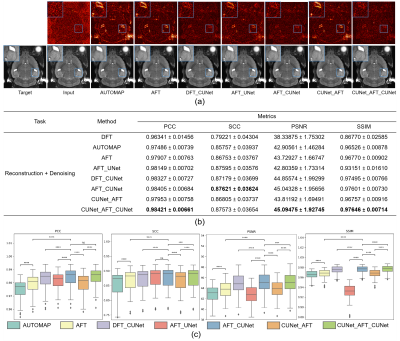
Figure 3: Qualitative comparison and quantitative comparison of different reconstruction plus denoising methods. (a) Reconstruction plus denoising results and residual maps on the real-world T2w dataset. (b) Table of metrics for different reconstruction plus denoising methods. We compare real-valued networks with complex-valued networks, AFT-based networks with DFT-based networks, and AFT-Net with non-AFT methods in terms of PCC, SCC, PSNR, and SSIM. (c) Boxplots of reconstruction plus denoising task in terms of PCC, SCC, PSNR, and SSIM with statistical paired t-test.

Figure 4: Qualitative and quantitative comparison of different reconstruction plus denoising methods evaluated on the dataset with simulated Gaussian noise, the dataset with different contrast caused by GBCAs, and the dataset with different contrast caused by different modalities. (a) Visual comparison of different reconstruction plus denoising methods. (b) Table of the performance metrics for different reconstruction plus denoising methods in terms of PCC, SCC, PSNR, and SSIM.
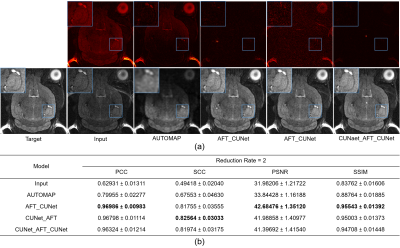
Figure 5: Qualitative and quantitative comparison of different reconstruction plus accelerated imaging methods evaluated on the real-world T2w MRI dataset with k-space data undersampled. (a) Visual comparison of different reconstruction plus accelerated imaging methods. (b) Table of the metrics for different reconstruction plus accelerated imaging methods in terms of PCC, SCC, PSNR, and SSIM.
DOI: https://doi.org/10.58530/2023/2935