Synopsis

Keywords: Image Reconstruction, Machine Learning/Artificial Intelligence, Unpaired unsupervised training, Transformer

In this abstract, we propose a novel deep-learning reconstruction method that enables training with only unpaired undersampled k-space data without the ground truth. The network utilizes a statistical model for the undersampling artifacts to enable unsupervised learning, and the generative adversarial network to enable unpaired training. In addition, the physics model is incorporated into the transformer network by unrolling the underlying optimization problem. Experiment results based on the fastMRI knee dataset exhibit marked improvements over the existing state-of-the-art reconstructions.

Introduction

Many studies have successfully applied deep learning in MR reconstruction from undersampled data^1-6. Most of them require a large number of labeled pairs for training a robust reconstruction network, which may be impractical for some MRI applications. In this work, we propose a novel unsupervised method for MRI reconstruction using only unpaired undersampled training data. Our network utilizes GAN^7-10 and a statistic model¹¹ to enable unpaired training without the ground truth data. Symmetric encoder-decoder architecture is used as the generator network in GAN, which is implemented by a vision transformer (ViT)¹² instead of the convolution neural network (CNN) to capture long-range dependencies. We also integrate such unpaired unsupervised training with Regularization by Denoising (RED)¹³ to incorporate the physics model into the network. The proposed method shows promising performance compared to the state-of-the-art methods.

Method

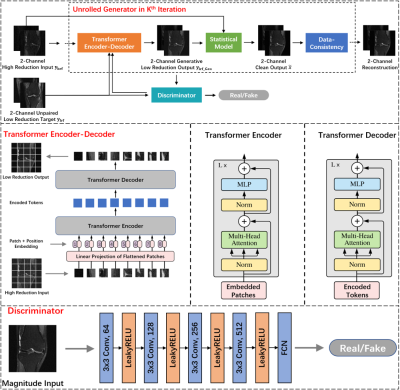
Our proposed method has an adversarial architecture⁷ with two parts as shown in Figure 1, the unrolled generator (G), and the discriminator (D). The network takes the 2-channel (real & imaginary) complex image with a high reduction factor as input and generates desired reconstructed image in the output. During the training, only undersampled images from high reduction and low reduction are needed without the need for fully sampled ground truth images (i.e., unsupervised), and they don’t have to be paired, meaning none of the training images need to be from the same object. The capability of unsupervised learning is achieved by a statistical model. Suppose we have two different acquisitions from an object. One is undersampled with low reduction, and the zero-filled image is defined as $$$y_{lrf} \equiv x+\mathcal{M} $$$, where x is the true image and $$$\mathcal{M}$$$ the noise-like artifacts. The other is further undersampled with an even higher reduction whose zero-filled image is represented as $$$y_{hrf} \equiv x+\mathcal{M} +\mathcal{N} $$$, where $$$\mathcal{M}$$$ and $$$\mathcal{N}$$$ are both noise-like artifacts independently drawn from a known sampling distribution $$$\mathcal{A}$$$. From a statistical point of view, the expectation of $$$y_{lrf}$$$ given $$$y_{hrf}$$$ can be described as $$\begin{equation}\mathbb{E}\left[ y_{lrf}\left.\right|y_{hrf}\right]=\mathbb{E}\left[ x\left.\right|y_{hrf}\right]+\mathbb{E}\left[ \mathcal{M}\left.\right|y_{hrf}\right]\tag{1}\end{equation}$$ We design the high and low reduction sampling masks such that artifacts $$$\mathcal{M}$$$ and $$$\mathcal{N}$$$ are independently and identically distributed, so they have the same expectation given $$$y_{hrf}$$$, $$$\mathbb{E}\left[ \mathcal{M}\left.\right|y_{hrf}\right]=\mathbb{E}\left[ \mathcal{N}\left.\right|y_{hrf}\right]$$$. Eq. (1) becomes $$\begin{equation}\begin{aligned}2\mathbb{E}\left[ y_{lrf}\left.\right|y_{hrf}\right]&= \mathbb{E}\left[ x\left.\right|y_{hrf}\right]+\left (\mathbb{E}\left[ x\left.\right|y_{hrf}\right]+ \mathbb{E}\left[ \mathcal{M}\left.\right|y_{hrf}\right] + \mathbb{E}\left[ \mathcal{N}\left.\right|y_{hrf}\right] \right )\\&=\mathbb{E}\left[ x\left.\right|y_{hrf}\right]+\mathbb{E}\left[ x+\mathcal{M}+\mathcal{N}\left.\right|y_{hrf}\right]\\&=\mathbb{E}\left[ x\left.\right|y_{hrf}\right]+y_{hrf}\end{aligned} \end{equation}\tag{2}$$ Therefore, the truth image x can be estimated by doubling the statistically estimated low-reduction image (from the high-reduction one) and subtracting the high-reduction image. The statistical estimation is implemented by a transformer encoder-decoder.
The above explains the paired case. To achieve unpaired training, GAN architecture is used to generate and discriminate the low-reduction image from a high-reduction input based on the statistical information obtained from the set of low-reduction images that are unrelated to the set of high-reduction inputs. Figure 1 illustrates the architecture of the proposed method where the kth iterations are unrolled to one training epoch. The unrolled generator consists of 3 modules: (1) Transformer encoder-decoder module implemented with a ViT architecture. (2) Statistical module which reconstructs the MR image by doubling the transformer’s low reduction output and subtracting its high reduction input. (3) Data-consistency module that incorporates the Fourier transform relationship in the network. Specifically, derived from the RED, the reconstruction is further updated as follows:$$\begin{equation} x=\left ( A^{H}A+\beta I \right ) ^{-1} \left (A^{H}y_{hrf}+\beta \tilde{x} )\right )\tag{3}\end{equation} $$ where $$$\tilde{x}$$$ is the output of the statistical module, A is the measurement matrix that contains the undersampling process and Fourier transform, and $$$\beta$$$ is a regulation factor. The loss for the generator is $$\begin{equation}\min_{\theta_{g}} \mathbb{E}\left [ \left \| y_{hrf} - G\left ( y_{hrf};\theta_{g} \right )\right \| _{2} -\lambda _{1}\mathbb{E}\left [ D\left ( G\left ( y_{hrf} \right ) ; \theta_{d} \right ) \right ] + \lambda _{2} \mathbb{E}\left [ \left \| y_{hrf} - x_{rec} \right \| _{2} \right ] \right ]\tag{4}\end{equation} $$ where G is the transformer encoder-decode with the parameter $$$\theta _{g} $$$, and D is the discriminator with parameter $$$\theta _{d} $$$, $$$x_{rec}$$$ is the final reconstruction after unrolled modules, $$$\lambda _{1}$$$ and $$$\lambda _{2}$$$ are the weights in the loss function. The discriminator loss is $$\begin{equation}\min_{\theta_{g}} \mathbb{E}\left [ D\left ( G\left ( y_{hrf} \right ) ; \theta_{d} \right ) \right ] -\mathbb{E}\left [ D\left ( y_{lrf};\theta _{d} \right ) \right ] +\eta \mathbb{E}\left [ \left ( \left \| \bigtriangledown_{\hat{y}_{hrf}} D\left ( \hat{y}_{hrf};\theta _{d} \right ) \right \| -1 \right ) ^{2} \right ] \tag{5}\end{equation}$$

Results

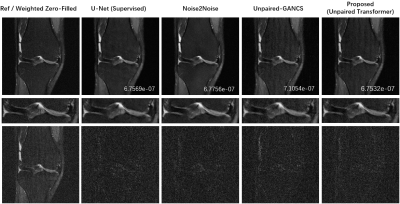
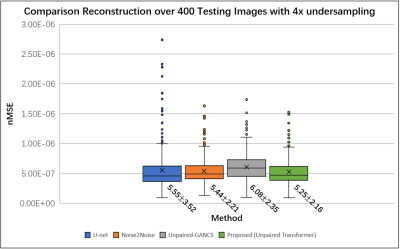
We used the raw single-coil k-space from the knee fastMRI dataset^14-15 that is available publicly at https://fastmri.org/. In particular, we randomly selected 200 sagittal knee MR scans and only 20 central images were selected for each subject that had anatomy, which gave a total of 4000 images for training. We further selected another 20 different subjects in the fastMRI dataset and picked 20 central images for each subject, which gave additional 400 images for testing. The training data and testing data have image size 320x320. All images are complex-valued.
Figure 2 shows reconstructions from 4× undersampled data using supervised U-net, unsupervised Noise2Noise, unpaired supervised GANCS, and proposed method with Transformer GAN. Figure 3 shows the boxplots of the normalized mean squared errors (nMSEs) of reconstructions for 400 testing images. It is seen that the reconstructions of the proposed method agree with ground truth image well.

Acknowledgements

This work was supported in part by the NIH/NIAMS R01 AR077452 and NIH U01 EB023829.