Synopsis

Keywords: Image Reconstruction, Machine Learning/Artificial Intelligence

Recovery with a self-calibrated denoiser (ReSiDe) is an unsupervised learning method based on the plug-and-play (PnP) framework. In ReSiDe, denoiser training and a call to the denoising subroutine are performed in each iteration of PnP. However, ReSiDe is computationally slow, and its performance is sensitive to the noise level selected to train the denoiser. Here, we extend ReSiDe from single-image to multi-image recovery (ReSiDe-M), improving both performance and computation speed. We also propose an auto-tuning method to select the noise level for denoiser training. Using data from fastMRI and MRXCAT perfusion phantom, we compare ReSiDe-M with other unsupervised methods.

Introduction

Most deep learning (DL) methods used for MRI reconstruction are based on supervised learning, requiring fully sampled training data. However, such training data may not be available for many applications. More recently, unsupervised learning methods have been proposed for MRI reconstruction. For example, deep image prior$$$^1$$$ trains a network on an image-specific basis and utilizes the network’s structure as a regularizer. Self-supervised learning via data undersampled (SSDU)$$$^2$$$ is another method that divides the measured data into two subsets, with one used as an input to the network and the other used to compute the loss. The plug-and-play (PnP) methods are inspired by the alternating direction method of multipliers (ADMM) and reconstruct images by iterating between data consistency and denoising. Training the denoiser in PnP requires access to high-quality images or image patches, which may not be available. We recently proposed recovery with a self-calibrated denoiser (ReSiDe)$$$^3$$$, which is an extension of PnP. ReSiDe operates on a single set of undersampled measurements and performs recovery by both training the denoiser and applying it to the image being recovered in each iteration of PnP. Computation time for ReSiDe can be prohibitively long for practical use. Here, we extend ReSiDe to a multi-image setup (called ReSiDe-M) to overcome this shortcoming.

Methods

ReSiDe-M is described in Algorithm 1. In the training phase, we utilize $$$N$$$ undersampled datasets. Recovering $$$N$$$ images entails solving $$$\tilde{A}\tilde{x} = \tilde{y}+\tilde{w}$$$, where $$$\tilde{A}$$$ is the forward operator for all $$$N$$$ images, $$$\tilde{x}$$$ and $$$\tilde{y}$$$ are the concatenation of $$$N$$$ images and measurements, respectively, and $$$\tilde{w}$$$ is complex-valued white Gaussian noise with variance, $$$\tilde{\sigma}^2$$$. During the $$$t^{th}$$$ iteration of the training process, we randomly extract $$$P$$$ patches from intermediate images, $$$\tilde{u}_t$$$, and add complex-valued white Gaussian noise of variance $$$\sigma^2_t$$$. The operator $$$\mathcal{I}_i[\cdot]$$$ describes the extraction of the $$$i^{th}$$$ patch, selected randomly from any of the $$$N$$$ images. Then, we train a convolutional neural network-based denoiser, $$$f(\cdot;\theta_t)$$$, parameterized by $$$\theta_t$$$, to remove the added noise. The network is trained using a supervised L2 loss ($$$\mathcal{L}$$$) between clean and noisy patches. With a known noise level, $$$\tilde{\sigma}^2$$$, e.g., from pre-scan data, we can adapt the added noise level, $$$\sigma^2_t$$$, based on the discrepancy principle. During the training, we save trained networks in each iteration, $$$t$$$. During testing, the series of denoisers can be sequentially applied in any PnP algorithm to recover an image. Note, the tilde-free operators in the test phase of Algorithm 1 operate on a single test image.
We evaluated the performance of ReSiDe-M in two studies. In the first study, we used T1 and T2 brain images from fastMRI$$$^4$$$. Sixteen multi-coil images with retrospective downsampling were used for training and five images were used for testing. The process was repeated for T1 and T2 images and for two different sampling patterns: pseudo-random GRO sampling pattern (S1)$$$^5$$$ and random sampling pattern (S2). Both sampling patterns were augmented with a 32-line wide fully sample region in the middle. The coil sensitivity maps were estimated using the method$$$^6$$$ by Walsh et al. ReSiDe-M was also evaluated in MRXCAT perfusion phantom$$$^7$$$, with 16 undersampled images used for training and five undersampled images used for testing. A spatiotemporal GRO sampling pattern (S3) was used for undersampling. All studies were performed at the acceleration rate of four.
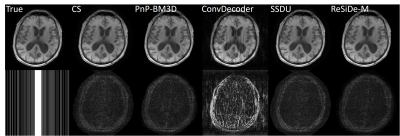
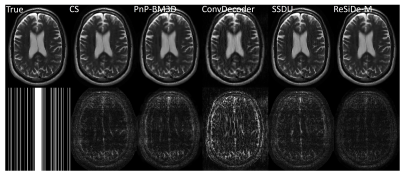
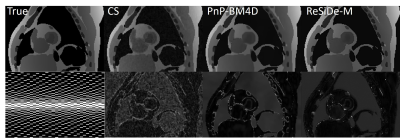
For brain images, $$$\tilde{\sigma}^2$$$ was estimated from the outer parts of k-space. For MRXCAT, the measurement noise variance, $$$\tilde{\sigma}^2$$$, was known. The value of, $$$\tau$$$, is a user-defined parameter that controls the image sharpness and noise tradeoff. We set $$$\tau = 0.7$$$. ReSiDe-M was compared to sparsity-based compressed sensing (CS), PnP with BM3D denoising, SSDU, and ConvDecoder$$$^8$$$ for brain imaging and to CS and PnP with BM4D denoising for MRXCAT.

Results

The reconstruction performance of ReSiDe-M is shown in Table 1. Each row displays the average normalized mean squared error (NMSE) and structural similarity index measure (SSIM) over five test datasets. For the brain dataset, ReSiDe-M outperforms traditional CS methods and unsupervised learning methods in both NMSE and SSIM. For the MRXCAT perfusion phantom study, ReSiDe-M also shows the advantage over CS and PnP-BM4D. During testing, the reconstruction time for ReSiDe-M was 12 s for brain imaging and 25 s for MRXCAT. In comparison, the reconstruction time for PnP-BM3D and PnP-BM4D was 36 minutes and 40 minutes, respectively. Representative images are shown in Figures 1-3.

Discussion and Conclusion

ReSiDe is an unsupervised learning method that reconstructs images by training a denoiser during the recovery process. The proposed extension, ReSiDe-M, utilizes ReSiDe during training to jointly reconstruct a small number of images from undersampled measurements. The denoisers trained during each iteration of training are saved. During the testing stage, the trained denoisers are used in a PnP algorithm for faster image recovery. Our results show that ReSiDe-M outperforms other unsupervised DL methods in terms of NMSE and SSIM. In terms of computation time during testing, ReSiDe-M is comparable to traditional CS methods and approximately two orders of magnitude faster than ReSiDe.

Acknowledgements

This work was funded by NIH projects R01EB029957 and R01HL151697