2930
Model-based neural ODE network for parallel MRI reconstruction1Department of Biomedical Engineering, Hankuk University of Foreign Studies, Yongin, Korea, Republic of
Synopsis
Keywords: Image Reconstruction, Parallel Imaging, Neural ODE
In parallel MRI, DNN-based models have recently outperformed conventional reconstruction techniques and can reconstruct high-quality MRI images, especially at high acceleration factors. We propose a model-based neural ODE network to reconstruct artifact-free MR images from under-sampled k-space data. We replaced the existing U-Net with a modified U-Net framework using neural ODEs with E2E-VarNet as the backbone. Our network solves unrolled iterations of reconstruction optimization with neural ODEs, and each neural ODE uses a gradient update step as a dynamics step. Our approach showed the improved reconstruction performance comparable to the SOTA method with few parameters.Introduction
Magnetic resonance imaging (MRI) is one of the widely-used medical imaging systems. Relatively long acquisition time for MRI is a major hurdle of achieving high spatial and temporal resolutions. Parallel imaging technique1,2, which reduces scan time by under-sampling the k-space data is essential for clinical scan. However, removing aliasing artifacts caused by under-sampling with high acceleration factors is challenging. Deep Neural Networks (DNN)-based models have recently outperformed conventional reconstruction techniques and can reconstruct high-quality MRI images, especially at high acceleration factors. After that, model-based deep learning designed for the inverse problem showed excellent performance by mathematically formulating the parallel MRI reconstruction as a forward model3-9. Among them, End-to-End Variational Network (E2E-VarNet)6 demonstrated the state-of-the-art (SOTA) performance by automating the entire parallel MRI reconstruction process, including deep learning-based sensitivity map estimation. Neural Ordinary Differential Equation (ODE) replaces DNN by a continuous model characterized by ODEs and has advantages over DNN in some tasks in addition to MRI reconstruction10-15.In this study, we propose a model-based neural ODE network to reconstruct artifact-free MR images from under-sampled k-space data. Our proposed approach expands the model-based deep learning architecture by using the ODE-based network. The application of neural ODE reduces the number of parameters and the memory occupied by the neural network while maintaining good performance.
Methods
Parallel MRI acquisition: In multi-coil MR signal acquisition, multi-receiver coils measure the signals affected by frequency domain's sensitivity profiles, called k-space. The MR image can be constructed by applying an inverse Fourier transform (IFT) to the measured k-space data. In parallel MRI, the relationship between the MR image and the measured k-space data can be defined as follows:$$k_{i}=MF(S_{i}x)+\epsilon_{i},\forall i=1,2,...,N,$$
where $$$k_{i}$$$ is the measured under-sampled k-space data in the $$$i$$$-th coil, $$$x$$$ is the MR image, $$$F$$$ is the Fourier transform (FT), $$$S_{i}$$$ is $$$i$$$-th coil sensitivity map, and $$$\epsilon$$$ is noise.
Neural ODE: Neural ODE formulates the forward pass of the DNN as the solution of the ODE. Residual neural networks such as ResNet16 can be modeled as a discretization of a continuous ODEs. The output of the $$$t$$$-th residual layer $$$f$$$ of residual networks with parameter $$$\theta$$$ is calculated as follows:
$$h_{t+1}=h_{t}+f(h_{t},\theta_{t}),$$
where $$$h_{t+1}$$$ and $$$h_{t}$$$ are the input and output of the $$$t$$$-th layer. By stacking infinitely many layers and limiting $$$\Delta t$$$ to 0, Above Eq. is replaced by an ODE defined by a neural network as follows:
$$\frac{\mathrm{d} h(t)}{\mathrm{d} t}=f(h(t),t,\theta).$$
The Euler discretization scheme of this ODE with step-size $$$\tau$$$ is as follows:
$$h_{t+1}=h_{t}+\tau f(h_{t},\theta_{t}),$$
which is nearly equivalent to the forward of the residual layer.
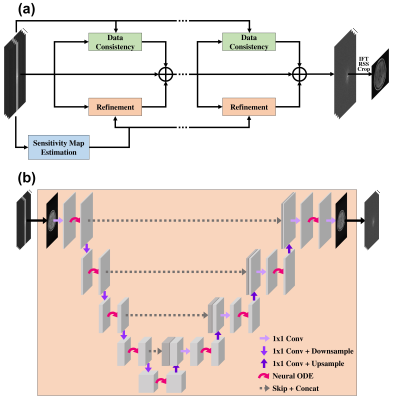
The reconstruction network: The backbone of our network architecture is based on the E2E-VarNet6, a model-based deep learning. The E2E-VarNet formulated an optimization problem about parallel MRI reconstruction and solved it by gradient descent methods. A gradient update step of the intermediate quantities was applied in k-space as follows:
$$k_{t+1}=k_{t}-\eta_{t}M(k_{t}-\tilde{k})+G(k_{t}),$$
G is the refinement module:
$$G(k_{t})=F\circ \mathcal{E}\circ CNN(\mathcal{R}\circ F^{-1}(k_{t})),$$
$$$\mathcal{E}$$$ and $$$\mathcal{R}$$$ are the coil sensitivity $$$expand$$$ and $$$reduce$$$ operators. U-Net17 is used for convolutional neural network (CNN). The final reconstructed image is calculated by a FT and root-sum-squares (RSS) reduction from reconstructed multi-coil k-space data.
The proposed approach: Our approach replaced the existing U-Net with the modified U-Net framework using neural ODEs15, as shown in Fig. 1. Our network solves unrolled iterations of reconstruction optimization with neural ODEs, and each neural ODE uses a gradient update step as a dynamics step. Also, in the E2E-VarNet, the number of trainable parameters increased as the number of iterations increased by using different CNN layers for each iteration. On the other hand, we shared the parameter weights across iterations. The sharing of weights prevents the risk of overfitting, which is particularly important in medical imaging with a limited dataset. We set the number of iteration blocks to 12 and used structural similarity (SSIM)18 loss function.
Experiments: To evaluate our approach, we compared with GRAPPA and E2E-VarNet. We used a subset of the NYU fast MRI brain dataset19. We used 16-coil T1-weighted images for all methods, 2886 slices for training and 910 slices for validation. The multi-coil k-space data were under-sampled using an equispaced sampling mask with the acceleration factors and ACS ratios: (4, 8%) and (8, 4%).
Results
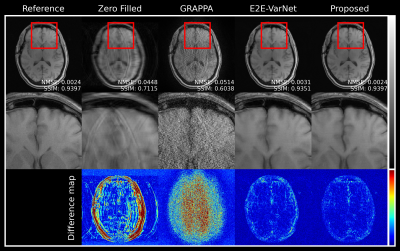
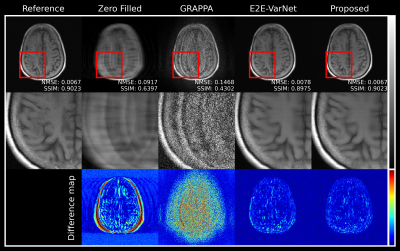
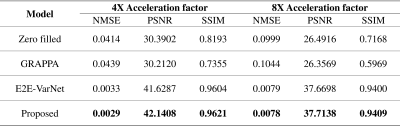
Figures 2 and 3 illustrate reconstructed MR images with acceleration factors 4 and 8, respectively. E2E-VarNet and our proposed approach generate high-quality MR images by reducing artifacts and noise. In addition, the reconstruction performance of the proposed approach are comparable to SOTA E2E-VarNet. The quantitative evaluations of the reconstructed images are summarized in table 1. Our approach has lower normalized mean square error (NMSE) and higher Peak Signal-to-noise Ratios (PSNR) and SSIM compared to other methods.Discussion and Conclusion
In this study, we proposed a model-based neural ODE network with a modified U-Net framework by using neural ODEs. Our approach showed the improved reconstruction performance comparable to the SOTA method with few parameters. However, an ODE-based network may require longer training time than the other deep learning methods. Other neural ODE structures for model-based deep learning may be more beneficial, and we will investigate suitable neural ODE structures in the future work.Acknowledgements
This work was supported by the MSIT (Ministry of Science, ICT), Korea, under the High-Potential Individuals Global Training Program (2021-0-01553), supervised by the IITP (Institute for Information & Communications Technology Planning & Evaluation), and the National Research Foundation of Korea (NRF) grant, funded by the Korean government (MSIT) (NRF-2020R1A2C4001623).References
1. Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: sensitivity encoding for fast MRI. Magn Reson Med. 1999;42(5):952-962.
2. Griswold MA, Jakob PM, Heidemann RM, et al. Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magn Reson Med. 2002;47(6):1202-1210.
3. Schlemper J, Caballero J, Hajnal JV, Price AN, Rueckert D. A deep cascade of convolutional neural networks for dynamic MR image reconstruction. IEEE Trans Med Imaging. 2018;37(2):491-503.
4. Hammernik K, Klatzer T, Kobler E, et al. Learning a variational network for reconstruction of accelerated MRI data: Learning a Variational Network for Reconstruction of Accelerated MRI Data. Magn Reson Med. 2018;79(6):3055-3071.
5. Aggarwal HK, Mani MP, Jacob M. MoDL: Model-based deep learning architecture for inverse problems. IEEE Trans Med Imaging. 2019;38(2):394-405.
6. Sriram A, Zbontar J, Murrell T, et al. End-to-end variational networks for accelerated MRI reconstruction. In: Medical Image Computing and Computer Assisted Intervention – MICCAI 2020. Springer International Publishing; 2020:64-73.
7. Jun Y, Shin H, Eo T, Hwang D. Joint deep model-based MR image and coil sensitivity reconstruction network (joint-ICNet) for fast MRI. In: 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR). IEEE; 2021.
8. Arvinte M, Vishwanath S, Tewfik AH, Tamir JI. Deep J-Sense: Accelerated MRI reconstruction via unrolled alternating optimization. Med Image Comput Comput Assist Interv. 2021;12906:350-360.
9. Lee JH, Kang J, Oh SH, Ye DH. Multi-domain Neumann network with sensitivity maps for parallel MRI reconstruction. Sensors (Basel). 2022;22(10):3943.
10. Chen RTQ, Rubanova Y, Bettencourt J, Duvenaud D. Neural ordinary differential equations. arXiv [csLG]. Published online 2018.
11. Yazdanpanah AP, Afacan O, Warfield SK. ODE-based deep network for MRI reconstruction. arXiv [eessIV]. Published online 2019.
12. Gholaminejad A, Keutzer K, Biros G. ANODE: Unconditionally accurate memory-efficient gradients for neural ODEs. In: Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence. International Joint Conferences on Artificial Intelligence Organization; 2019.
13. Dupont E, Doucet A, Teh YW. Augmented Neural ODEs. arXiv [statML]. Published online 2019.
14. Zhang T, Yao Z, Gholami A, et al. ANODEV2: A coupled neural ODE evolution framework. arXiv [csLG]. Published online 2019.
15. Pinckaers H, Litjens G. Neural Ordinary Differential Equations for semantic segmentation of individual colon glands. arXiv [eessIV]. Published online 2019.
16. He K, Zhang X, Ren S, Sun J. Deep residual learning for image recognition. In: 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). IEEE; 2016.
17. Ronneberger O, Fischer P, Brox T. U-Net: Convolutional Networks for Biomedical Image Segmentation. In: Lecture Notes in Computer Science. Springer International Publishing; 2015:234-241.
18. Wang Z, Bovik AC, Sheikh HR, Simoncelli EP. Image quality assessment: from error visibility to structural similarity. IEEE Trans Image Process. 2004;13(4):600-612.
19. Zbontar J, Knoll F, Sriram A, et al. FastMRI: An open dataset and benchmarks for accelerated MRI. arXiv [csCV]. Published online 2018.
Figures