2928
Posterior Sampling for Accelerated Multicoil MRI Reconstruction using a Conditional Normalizing Flow
Jeffrey Wen1, Rizwan Ahmad2, and Philip Schniter1
1Electrical Engineering, The Ohio State University, Columbus, OH, United States, 2Biomedical Engineering, The Ohio State University, Columbus, OH, United States
1Electrical Engineering, The Ohio State University, Columbus, OH, United States, 2Biomedical Engineering, The Ohio State University, Columbus, OH, United States
Synopsis
Keywords: Image Reconstruction, Machine Learning/Artificial Intelligence
For accelerated MR image reconstruction, machine learning (ML)-based methods outperform traditional sparsity-based methods by exploiting large datasets to learn effective priors. However, most ML methods output only a single image reconstruction when in fact there may be many plausible reconstructions given the measurement and prior. To extract this diagnostically relevant information, we propose to explore the space of plausible images, i.e., to sample the posterior, using ML. Among ML methods, conditional normalizing flows (CNFs) stand out for rapid sample generation and simple likelihood-based training. In this work, we present the first CNF for posterior sample generation in accelerated multicoil MRI.Introduction
Accelerated magnetic resonance imaging (MRI) seeks to reduce acquisition time while preserving diagnostically relevant information1. As an ill-posed inverse problem though, many possible reconstructions are consistent with the measurements and prior. Considering the consequential nature of MRI, generating many posterior samples could be very beneficial. Among methods for posterior sample generation, conditional normalizing flows (CNFs)2 stand out for offering rapid inference with simple likelihood-based training and outperforming other methods in a recent super-resolution contest3. Previous work on CNFs for MRI by Denker et al.4 demonstrated promising initial results but was limited to single-coil magnitude measurements. We develop a CNF that works with complex multicoil MRI measurements and leverages recent CNF advances to demonstrate excellent performance across multiple performance metrics.Methods
DataWe use non-fat-suppressed fastMRI5 knee data, giving 17 286 training and 3 592 validation images. For preprocessing, each measurement stack is compressed to c=2 complex-valued virtual coils6 and cropped to 320 × 320 pixels. Sampling uses a fixed golden ratio offset (GRO)7 Cartesian mask with acceleration 4 and a 13 pixel wide autocalibration signal (ACS) region. Coil-sensitivity maps are estimated using ESPIRiT8. All inputs are normalized by the 95th percentile of the zero-filled (ZF) magnitude image before being used by the networks.
Architecture
Our CNF consists of a conditional invertible neural network (cINN) G and a conditioning network H. H accepts measurement information and converts it into a form that is usable by G. Given the conditioning information, G maps Gaussian random vectors to posterior samples.
For G, we use multi-scale RealNVP9 with l = 3 downsampling layers, m = 15 flow steps per layer, and a transition step at the beginning of each layer to ease the dimensionality change between layers10. For H, we use the UNet from Zbontar et al.5 (with 128 output channels in the first convolution block and 4 pooling layers) and configure it to accept a ZF c-coil image and generate feature maps that are concatenated with the inputs to G’s coupling layers.
We train G to map the non-measured-subspace projections of the c-coil complex ground-truth images to Gaussian random vectors. This allows the cINN to focus on learning the unknown data. During inference, our cINN maps Gaussian random vectors to these “inverse-zero-filled” images, which are then combined with the measured information to yield the final (data-consistent) predictions. Our data-consistency method is reminiscent of “frequency separation” from Song et al.11 but operates in the complex domain. Our architecture is illustrated in Figure 1.
Baseline
We compare to the single-coil CNF from Denker et al.4 To convert our multicoil measurements to a format usable by that method, we coil-combine the ZF multicoil images using the estimated coil maps. We use a similar technique to create single-coil ground-truth training data.
Training
We first train the UNet for 50 epochs to recover the multicoil ground-truth. In particular, we train the UNet to minimize squared-error in the non-measured subspace and replace the measured subspace with the measured data. Next, the UNet and cINN are jointly trained for 100 epochs to minimize the standard negative log-likelihood loss2 with batch size 16. We train Denker et al.4 for 300 epochs.
Metrics
All images are unnormalized and converted to the magnitude domain before metrics are calculated. When computing Fréchet Inception Score (FID)12 and conditional FID (cFID)13, we use VGG-16 embeddings14 and 8 posterior samples per validation image. When computing normalized mean-squared error (NMSE), peak-signal-to-noise ratio (PSNR), and structural-similarity index (SSIM), we use mean images computed from p = 50 posterior samples.
Results/Discussion
Figure 2 shows average performance over the validation set and Figures 3 and 4 show typical image recoveries. Relative to the Denker’s single-coil CNF4, our multicoil CNF shows significant improvements in all metrics and fewer reconstruction artifacts in the generated images. The posterior standard-deviation maps in Figure 4 provide insight into where recovery uncertainty may exist. Figure 5 shows that both CNFs achieve the expected amount of PSNR gain15 as a function of the number of averaged samples, p, which suggests that both methods achieve the proper tradeoff between accuracy and diversity. Future studies will focus on optimizing the architectures of G and H and validating CNF in different MRI applications.Conclusion
We propose the first CNF for posterior sampling in multicoil accelerated MRI. By leveraging recent advances in CNF, we demonstrate improvement over the previous single-coil, magnitude image applications. The generated posterior samples and standard-deviation maps, unavailable with point-estimate methods, provide additional diagnostic and trustworthiness resources for clinicians.Acknowledgements
This work was funded by NIH project R01EB029957.References
- Lustig M, Donoho D, Pauly JM. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn. Reson. Med. 2007;58:1182-1195.
- Papamakarios G, Nalisnick ET, Rezende DJ, Mohamed S, Lakshminarayanan B. Normalizing Flows for Probabilistic Modeling and Inference. J. Mach. Learn. Res. 2021;22:1-64.
- Lugmayr A, Danelljan M, Timofte R, et al. NTIRE 2022 challenge on learning the super-resolution space. In: Proc. IEEE Conf. Comp. Vision Pattern Recog.:786–797 2022.
- Denker A, Schmidt M, Leuschner J, Maass P. Conditional Invertible Neural Networks for Medical Imaging. J. Imaging. 2021;7:243.
- Zbontar J, Knoll F, Sriram A, et al. fastMRI: An Open Dataset and Benchmarks for Accelerated MRI. arXiv:1811.08839. 2018.
- Zhang T, Pauly JM, Vasanawala SS, Lustig M. Coil compression for accelerated imaging with Cartesian sampling. Magn. Reson. Med. 2013;69:571-582.
- Joshi M, Pruitt A, Chen C, Liu Y, Ahmad R. Technical Report (v1.0)–Pseudo-random Cartesian Sampling for Dynamic MRI. arXiv:2206.03630.2022.
- Uecker M, Lai P, Murphy MJ, et al. ESPIRiT–An eigenvalue approach to autocalibrating parallel MRI: Where SENSE meets GRAPPA. Magn. Reson. Med. 2014;71:990–1001.
- Dinh L, Sohl-Dickstein J, Bengio S. Density estimation using Real NVP. In: Proc. Int. Conf. on Learn. Rep. 2017.
- Lugmayr A, Danelljan M, Van Gool L, Timofte R. SRFlow: Learning the Super-Resolution Space with Normalizing Flow. In: Proc. European Conf. Comp. Vision. 2020.
- Song KU, Shim D, Kim Kw, Lee Jy, Kim Y. FS-NCSR: Increasing Diversity of the Super-Resolution Space via Frequency Separation and Noise-Conditioned Normalizing Flow. In: Proc. IEEE Conf. Comp. Vision Pattern Recog. Workshop.:968-977 2022.
- Heusel M, Ramsauer H, Unterthiner T, Nessler B, Hochreiter S. GANs Trained by a Two Time-Scale Update Rule Converge to a Local Nash Equilibrium. In: Proc. Neural Inf. Process. Syst. Conf.;30 2017.
- Soloveitchik M, Diskin T, Morin E, Wiesel A. Conditional Frechet Inception Distance. arXiv:2103.11521. 2021.
- Kastryulin S, Zakirov J, Pezzotti N, Dylov DV. Image Quality Assessment for Magnetic Resonance Imaging. arXiv:2203.07809. 2022.
- Bendel M, Ahmad R, Schniter P. A Regularized Conditional GAN for Posterior Sampling in Inverse Problems. arXiv:2210.13389. 2022.
Figures

Figure 1: The architecture of our CNF. The conditioning network takes in multicoil zero-filled measurements and outputs features used by the cINN. The cINN learns an invertible mapping between Gaussian random samples and images that are the projection of the ground-truth onto the non-measured subspace.

Figure 2: Quantitative results on non-fat-suppressed fastMRI knee data. We report the mean and standard error across all validation volumes. Our multicoil CNF outperforms the single-coil CNF in all metrics.
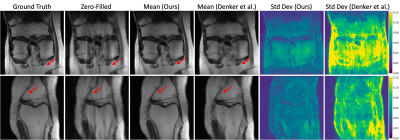
Figure 3: Mean images and pixel-wise standard-deviation maps computed from 50 posterior samples. The standard-deviation maps show which pixels have the greatest reconstruction uncertainty. The mean images from our multicoil CNF show fewer artifacts than those from the single-coil CNF.
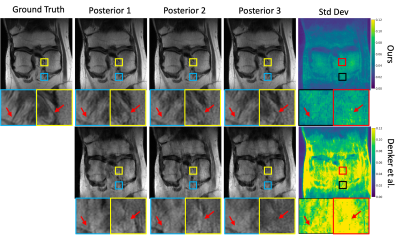
Figure 4: Examples of posterior samples and standard-deviation maps, both with zoomed regions. The standard-deviation map provides extra information about high-variability areas for clinicians.
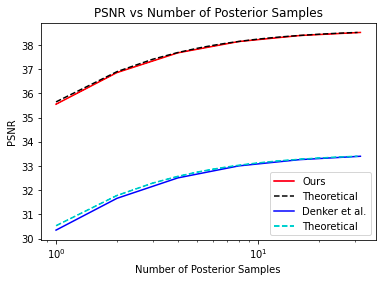
Figure 5: The PSNR of the p-sample mean image versus p. The empirical performance on validation data is shown with solid lines and the theoretical growth curves are shown with dashed lines. Note the expected 3 dB increase as p grows from 1 to infinity.
DOI: https://doi.org/10.58530/2023/2928