Synopsis

Keywords: Image Reconstruction, Machine Learning/Artificial Intelligence

Model-based Deep Unrolled Networks offer high quality reconstructions but the performance degrades if any mismatch occurs in acquisition settings. Different networks for different acquisition settings require extensive training data, in addition to making the clinical deployment difficult. We propose a single unrolled deep-learning algorithm called as Ada-MoDL, whose parameters are conditioned on the acquisition information (metadata) of a dataset, using a Multi-Layer Perceptron (MLP) that maps the metadata to network parameters. Ada-MoDL outperforms models trained for a specific acquisition setting or a single model trained with all the available contrasts, when the training data in each acquisition setting is limited.

Introduction

A typical MRI protocol consists of different sequences, each acquiring data with different settings. The current practice is to highly undersample each of the datasets, followed by recovery using constrained reconstruction algorithms [1-3]. Deep Unrolled (DU) optimization schemes have become state-of-the-art for MRI recovery, producing impressive image quality at high acceleration factors [4-7]. Because the performance of DU algorithms degrade when the acquisition physics is different from the one they are trained with [8], different trained networks are needed for each of the sequences. In this work, we introduce a single unrolled deep-learning (DL) algorithm termed as Ada-MoDL, which adapts to multiple acquisition settings and eliminates the need for acquisition specific models. The proposed architecture consists of a multi-layer perceptron (MLP) that conditions the CNN parameters on acquisition metadata of a dataset including contrast, scanner field-strength, and acceleration. Our preliminary experiments show either improved or at par performance with acquisition specific models. The proposed conditional framework outperformed the traditional unrolled models trained for each acquisition setting.

Theory

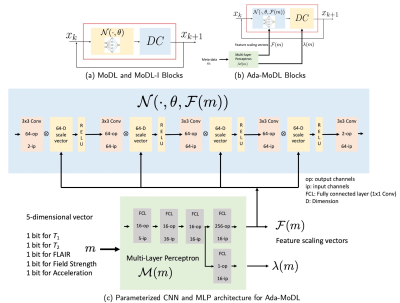
An image $$$\mathbf x \in \mathbb C^N$$$ to be recovered from noisy under-sampled measurements $$$\mathbf b$$$ , obtained through Parallel MRI acquisition as, $$$\mathbf b = \mathcal A(\mathbf x) + \mathbf n$$$ where $$$\mathcal A$$$ is a linear operator embedding coil sensitivities, Fourier transform operator and sampling mask while $$$\mathbf n$$$ is white Gaussian noise. MoDL [4] is a DU framework, solving the inverse problem by alternating between data-consistency (DC) and a CNN in $$\arg \min_{x} \frac{\lambda}{2}\|\mathcal A(\mathbf x) - \mathbf b\|_2^2 + \|\mathcal N(\mathbf x, \theta)\|_2^2$$, where $$$\mathcal N$$$ is a CNN with weights $$$\theta$$$. Such networks show degradation in performance when tested on unseen acquisition settings.
We circumvent the above limitation by proposing a conditional network to solve, $$\arg \min_{x} \frac{\lambda(m)}{2}\|\mathcal A(\mathbf x) - \mathbf b\|_2^2 + \|\mathcal N(\mathbf x, \theta, \mathcal F(m))\|_2^2$$ where $$$\mathcal M(m) = [\mathcal F(m), \lambda(m)]$$$ is an MLP, mapping acquisition information $$$m$$$ to the regularization weighting $$$\lambda(m)$$$ and a vector $$$\mathcal F(m)$$$ (Fig. 1(b)). $$$\mathcal F(m)$$$ contains scaling factors to weigh the features generated by the intermediate convolution layers of $$$\mathcal N(\cdot, \theta, \mathcal F(m))$$$, as shown in Fig. 1(c). Since network parameters and generated features are expected to vary with contrast, field strength, acceleration etc., the MLP ensures regularization strength $$$\lambda(m)$$$ and weights in $$$\mathcal F(m)$$$ vary according to metadata $$$m$$$. The network alternates between $$\mathbf z_k = \mathcal D(\mathbf x_k, \theta, \mathcal F(m))$$, and $$\mathbf x_{k+1} = (\mathcal I + \lambda(m) \mathcal A^H \mathcal A)^{-1}(\lambda(m)\mathcal A^H\mathbf b + \mathbf z_k), hspace{6pt} k=1,2,...,K$$ where $$$\mathcal D(\mathbf x, \theta, \mathcal F(m)) = \mathbf x - \mathcal N(\mathbf x, \theta, \mathcal F(m))$$$ and $$$K$$$ is total number of unrolls. Similar to CNN weights, $$$\lambda(m)$$$ and $$$\mathcal F(m)$$$ are shared across iterations. The CNN and MLP weights are jointly optimized by training the network end-to-end.

Experiments and Results

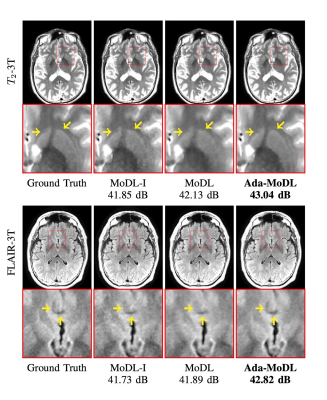
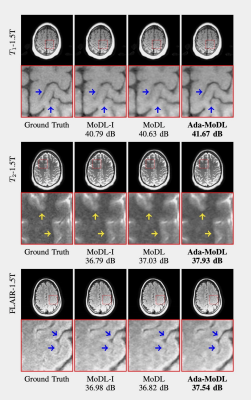
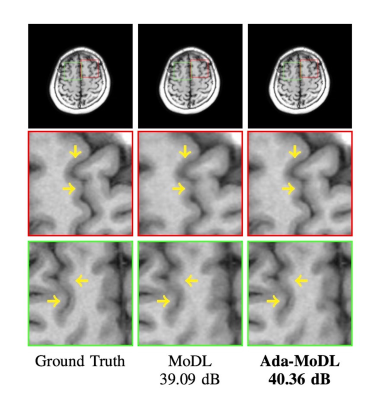
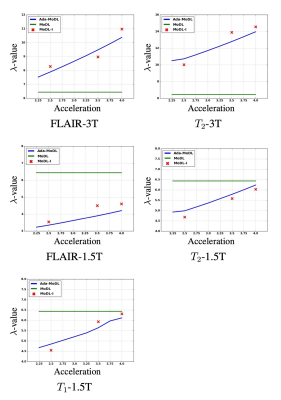
Fully sampled data with contrasts $$$T_1, T_2, FLAIR$$$, were collected on an Orian 1.5T and a Galan 3T MRI using a 16-channel head coil (Canon Medical Systems Corporation, Tochigi, Japan). The acquisition is 2D multi-slice. Training datasets were created with $$$T_1-1.5T, T_2-1.5T, FLAIR-1.5T, T_2-3T, FLAIR-3T$$$ contrasts. $$$T_1-3T$$$ data was used only to test performance. We choose $$$N$$$ as a 5-layer CNN. Ada-MoDL has 5% additional training parameters (from MLP) over MoDL and MoDL-I. During training, each of the datasets was retrospectively under-sampled for four accelerations (1.8x, 2.5x, 3.5x and 4.0x), resulting in 20 acquisition settings. The metadata $$$m$$$ is a 5-dimensional vector with a bit each for $$$T_1, T_2, FLAIR$$$, field strength and acceleration. We trained 3-iteration models of Ada-MoDL, MoDL and MoDL-I (Fig. 1(a)) for comparisons. MoDL is a single network trained with data available from multiple contrasts while MoDL-I is trained for every acquisition setting. The training data consists of one subject per contrast for studying performance with limited data availability.
Results are shown in Fig. 2,3, and 4. Ada-MoDL outperforms MoDL and MoDL-I for every acquisition setting. MoDL-I performs poorly due to lack of data even though it is trained with a specific contrast. The added flexibility in Ada-MoDL ensures optimality in trained parameters with respect to variation in acquisition while MoDL performance degrades due to same parameters for all settings. On unseen $$$T_1-3T$$$ contrast too, Ada-MoDL outperforms MoDL, preserving features better. We study the values mapped by the MLP in Fig. 5. It is observed that follows the trend in MoDL-I, thus proving adaptability in learning optimal for each setting. Overall, Ada-MoDL performs better on multiple acquisition settings even with limited available data from each of them.

Conclusion

We introduced a conditional deep unrolled framework termed as Ada-MoDL for parallel MRI reconstruction of datasets acquired with different acquisition conditions. Unlike traditional DU networks, it learns the network parameters as a function of acquisition information of a dataset. The parameters are modulated by the acquisition information through an MLP to provide optimal recovery for each setting. Ada-MoDL offers improved performance compared to training MoDL for each kind of acquisition. Ada-MoDL can also extrapolate the network to acquisition settings that were not included in the training dataset. The proposed single-network architecture would make more efficient deployment of unrolled networks in clinical setup.

Acknowledgements

This work was supported by Canon Medical Research USA.The authors thank Kensuke Shinoda (Canon Medical Systems Corporation) for sharing a dataset that was used in this work.