Synopsis

Keywords: Image Reconstruction, Machine Learning/Artificial Intelligence

For magnetic resonance (MR) image reconstruction, Fourier-domain measurements are collected at rates far below Nyquist to reduce clinical exam time. Because many plausible reconstructions exist that are consistent with a given measurement, we use machine learning to sample from the posterior distribution rather than generate a single image reconstruction. Many such works leverage score-based generative models (SGMs), which seek to iteratively denoise a random input but require many minutes to generate each sample. We propose a conditional generative adversarial network (GAN) that generates hundreds of posterior samples per minute and outperforms the current state-of-the-art SGM for multi-coil MR posterior sampling.

Introduction

In accelerated magnetic resonance imaging (MRI), measurement data is severely undersampled in order to reduce acquisition time. Due to the ill-posed nature of this inverse problem, there exist many plausible reconstructions for any given set of measurements. Many deep learning-based techniques seek to generate a single "best" estimate (e.g., MAP or MMSE). However, there is a growing interest in sampling from the full posterior distribution. State-of-the-art score-based generative models (SGMs)^1,2 do this but are impractical due to long sampling time (tens of minutes). Alternatively, conditional generative adversarial networks (cGANs) have been proposed to generate posterior samples^3,4. However, cGANs often succumb to mode collapse, causing their samples to lack diversity. We propose a novel cGAN regularization technique that encourages the generated distribution to agree with the correct posterior in mean and trace-covariance. We validate our technique on $$$R=4$$$ acceleration multi-coil MRI reconstruction and show that we outperform competitors in all tested metrics.

Methods

Regularization
When training the generator, we add supervised $$$\ell_1$$$ loss and an appropriately weighted standard-deviation reward. Leveraging the fact that $$$\mathcal{E}_1/\mathcal{E}_P=2P/(P+1)$$$, where $$$\mathcal{E}_P$$$ is the sum-squared error between the $$$P$$$-sample-averaged reconstruction and the ground truth, we adjust the reward weight during training so that this relationship holds on validation data. Figure 1 shows a compact summary of our proposed approach.

Data
For evaluation, we use the first 8 slices from each volume of T2 fastMRI brain data⁵, yielding 12200 training, 784 validation, and 2376 testing images. We compress each set of measurements into 8 complex virtual coils⁶ and crop all images to 384$$$\times$$$384 pixels. All data is then undersampled using a fixed Golden Ratio Offset (GRO)⁷ sampling mask with an acceleration of 4 and 32-line wide autocalibration signal (ACS) region. The multi-coil zero-filled images are used as input to our generator and discriminator. We combine the coils of our samples via ESPIRiT-estimated⁸ coil sensitivity maps (via SigPy⁹) during validation and testing.

Architecture
Our discriminator is a convolutional neural network (CNN), and our generator is a U-Net⁵ with 128 initial channels and 4 pooling layers that outputs complex 8-coil images. We use patch-based discrimination¹⁰ since it gave slightly improved performance. To handle multi-coil data, the input to our generator has 16 image channels. The first 8 channels correspond to the real part of the coil images and the last 8 correspond to the imaginary part. Our generator input also includes 2 noise channels, where we inject zero-mean unit-variance Gaussian noise. For the input to our discriminator, we concatenate the zero-filled coil images with the corresponding ground truth or reconstruction, yielding 32 input channels.

Competitors
We compare to the SGM proposed by Jalal et al.¹ and the regularized cGANs proposed by Adler et al.³ (which uses a 2-sample discriminator) and Ohayon et al.⁴ (which uses supervised $$$\ell_2$$$ generator regularization). For the SGM, we use the authors' original implementation¹¹ except for the sampling mask.The cGAN techniques differ only in generator regularization.

Training
Each cGAN was trained to minimize the WGAN-GP objective¹² (plus any generator regularization) for 100 epochs. The models were trained using 4 NVIDIA A100 GPUs, each with 82GB of memory. Training took roughly 2.5 days for each.

Metrics
We report peak-signal-to-noise ratio (PSNR) and structural-similarity index measure (SSIM) on images that are the average of $$$P=$$$ 32 generated samples. We also compute the Frechet Inception Distance (FID)¹³ and conditional FID (CFID)¹⁴ using VGG-16 embeddings¹⁵ and $$$P=$$$ 32 samples per image. We also report the average pixel-wise standard deviation (APSD) computed using $$$P=$$$ 32 samples per image. To facilitate comparison with the SGM, which is very slow to generate samples, we test using a randomly selected 72-image subset of our test set to compute the aforementioned metrics. For the cGANs, CFID was also evaluated on all 2376 test images, and again on all 14576 training and test images, since using more samples reduces bias¹⁴.

Results & Discussion

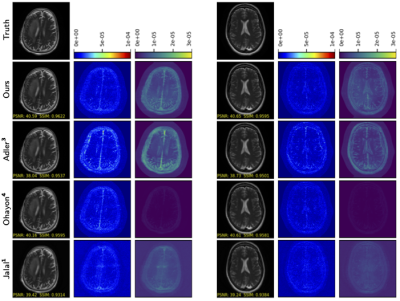
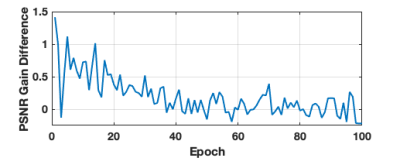
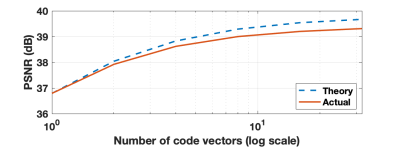
Metrics for the four approaches under test are reported in Table 1. Our approach gave significantly better CFID and FID than the competitors. It also gave the highest PSNR and SSIM, although both were within one standard error of those achieved by Ohayon et al. We don't consider APSD as a performance metric, but we note that Ohayon et al.'s APSD was almost two orders of magnitude lower than those of the other approaches, indicating mode collapse. Additionally, the cGANs generated samples 3800 times faster than Jalal et al.'s SGM. Example reconstructions are shown in Figure 2.

Results for our auto-tuning procedure can be seen in Figures 3 and 4. Figure 3 shows that, as training progresses, the dB difference between the target and measured PSNR gain $$$\mathcal{E}_1/\mathcal{E}_P$$$ tends toward 0. Similarly, Figure 4 shows that our final trained generator produces samples that closely align with the target PSNR-gain curve.

Conclusion

We proposed a novel cGAN regularization technique consisting of supervised $$$\ell_1$$$ loss with an appropriately weighted standard-deviation reward. Experiments on T2 fastMRI brain data show our method outperforming existing cGANs and a state-of-the-art SGM in $$$R=$$$ 4 acceleration multi-coil reconstruction.

Acknowledgements

This work was funded by the National Institutes of Health under grant R01-EB029957.