2925
Deep Unfolding MR reconstruction - weighting the k-space sampling Density in training Loss (wkDeLo)1Washington University in Saint Louis, Saint Louis, MO, United States, 2Engineering - Computer Science and Engineering, Washington University in Saint Louis, Saint Louis, MO, United States, 3Neurology, Washington University in Saint Louis, Saint Louis, MO, United States, 4Radiology - Main - Research - Radiological Sciences, Washington University in Saint Louis, Saint Louis, MO, United States, 5Radiology - Research Imaging Facilities - MR Facility, Washington University in Saint Louis, Saint Louis, MO, United States, 6Radiology - Main - Research - Radiological Sciences - Biomedica, Washington University in Saint Louis, Saint Louis, MO, United States, 7Surgery - Plastics, Washington University in Saint Louis, Saint Louis, MO, United States, 8Engineering - Electrical & Systems Engineering, Washington University in Saint Louis, Saint Louis, MO, United States
Synopsis
Keywords: Image Reconstruction, Image Reconstruction
We develop a self-supervised and physics-guided deep unfolding (DU) network for MR image reconstruction by weighting the k-space sampling Density in network training Loss (wDeLo). We have demonstrated that high-quality MR images at a spatial resolution of 0.6x0.6x0.8 mm3 could be achieved using an acquisition time of 1 minute (x6.25 acceleration) or 45 seconds (8x acceleration). Compared to SSDU and its uniform weighted counterpart (un-wDeLo), the wDeLo method significantly improves PSNR and SSIM. It had fewer artifacts, lower noise, and preserved image sharpness.Introduction
High-resolution 3D MRI acquisition is time-consuming 1-4. Deep-learning MR reconstruction methods can accelerate MR acquisition 5-17. The Model-based reconstruction with Deep Learned Priors (MoDL) method reduces artifacts and noise. MoDL accounts for the physics model of the imaging system (physics-based) through data consistency (DC), and it employs deep learning priors in regularization. Deep unfolding (DU) has been proposed to perform a fixed number of iterations by alternating between DC and regularization in end-to-end training. The Self-Supervised learning via Data Under-sampling (SSDU) 18 method is a DU method trained without ground truth.In accelerated MRI, variable density k-space samplings have been widely utilized. In Cartesian sampling, the low k-space is fully covered as auto-calibrated signal lines, while the outer k-space was sampled more sparsely 19. Radial and spiral sequences inherently sample the k-space center more densely than the outer k-space 20. Existing methods, including SSDU, have not yet accounted for variable sampling density in the MoDL network training.We developed a self-supervised and physics-guided DU network by weighting the k-space sampling Density in network training Loss (wkDeLo) and utilized wkDeLo to accelerate the stack-of-stars MRI for high-resolution 3D cranial bone imaging. We demonstrated high-quality MR images at a spatial resolution of 0.6x0.6x0.8 mm3 could be achieved using an acquisition time of 1 minute (x6.25 acceleration) or 45 seconds (8x acceleration).Method
MRI scans were obtained from 39 pediatric participants using a Golden Angle stack-of-stars sequence with the following imaging parameters: TE/TR = 2.47ms/4.84ms, flip angle = 4°, BW = 410 Hz/pixel, FOV = 192 mm, 224 slices, voxel size 0.6x0.6x0.8 mm3, number of radial spokes = 400, and total acquisition time = 5:04 min.A classic physics-guided reconstruction regularized by a deep learning prior reconstructs MR images by iteratively minimizing a loss function as depicted below
I=argminI ∑i∑j||Hi,j∙I-Ki,j ||22 +h(I) (1)
h(I)=λm /2 ‖ IT(I-Rθ (I)) ‖1 (2)
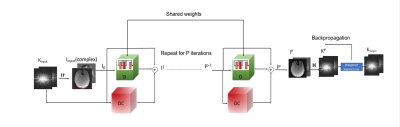
where the operator ; F is the multicoil nonuniform forward Fourier transform (MCNU-FFT) operator; Cj is the coil sensitivity for Coil j; S is the sampling function; I is the to-be-determined image; Ki,j is the acquired k-space data for spoke i with coil j. The first term of the cost function is to ensure DC, while the second term h(I) is a regularization term. is the transpose of and lm is the regularization coefficient learned during the DU network training. is a convolution neural network with dual-channel inputs for real and imaginary parts of the complex images.
In the proposed wkDeLo method, the L1-loss is
argmin ∑ W*||Hj,j IP -Ktarget ||
where W is the weight to account for k-space sampling density variations with small values in the low k-space and large values in the high k-space. Moreover, SSDU and a method with uniformly weighted k-space in the training loss (un-wkDeLo) are included for comparison. Using the images reconstructed from a 5-min scan as the gold standard, we computed SSIM and PSNR for reconstructed images from 1-min and 45 seconds k-space data using SSDU, un-wkDeLo, and wkDeLo.The DU architecture consists of the DC and =I- blocks as demonstrated in Figure 1. During the training, the k-space data from 400 radial spokes (5 min scan) can be divided into two disjoint data sets: the first 80 radial spokes as Kinput and the remaining 320 spokes as Ktarget. Kinput is transformed into the spatial domain (Iinput) via an inverse Fourier H†. The complex Kinput and Iinput were then fed into the DU network for P iterations. IP is the output of DU. The forward Fourier H transforms IP to k-space Kp and the weighted difference between Kp and Ktarget is used in the DU training loss.
Results
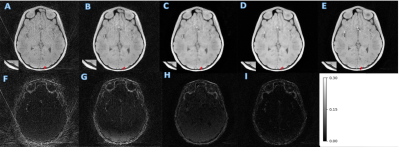
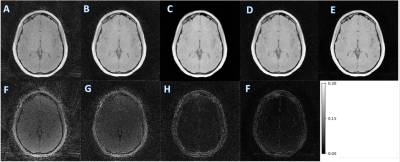
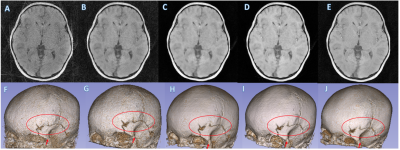
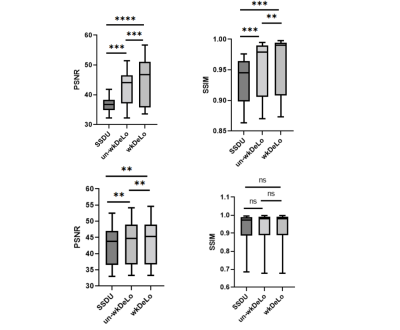
MCNUFFT, SSDU, un-wkDeLo, and wkDeLo were used to reconstruct 1-minute and 45 seconds k-space data. MCNUFFT has high noise and reconstruction artifacts (Figure 2,3A), 1-min SSDU improve images, but there are still visible artifacts (Figure 2,3B). Un-wkDeLo has further reduced noise and artifacts but at the expense of image sharpness, resulting in lower visibility of small structures (Figure 2,3C). The proposed wkDeLo effectively reduces artifacts and noise, while still preserving fine details of the structures (Figure 2,3D). Difference images compared to the gold standard reference are shown in the second row (Figure 2,3F, G, H, and I).Volumetric and 3D rendered cranial images from a trauma patient with fracture (Figure 4) are shown. The 3D rendered images were created from inverted MR images using 3D Slicer. High-resolution 1-min MR inverted images generated by our proposed method produced similar suture visibility compared to 5-min MCNUFFT. The SSIM and PSNR of the wkDeLo images are significantly higher than SSDU and un-wDeLo (Figure 5).Discussion and Conclusions
We developed a wkDeLo method to obtain 3D submillimeter resolution MR in under 1 minute with significantly higher PSNR and SSIM than SSDU and un-wkDeLo. It had fewer artifacts and lower noise. wkDeLo images preserve image sharpness to see small structures. Our results demonstrate k-space sampling density variations should be accounted for in DU network training. The wkDeLo method can be extended to spiral or variable density Cartesian k-space sampling schemes.Acknowledgements
This work was supported by grants from the National Institutes of Health (NIH) R01 EB032713References
1. Block KT, Uecker M, Frahm J. Undersampled radial MRI with multiple coils. Iterative image reconstruction using a total variation constraint. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 2007;57(6):1086-1098.
2. Griswold MA, Jakob PM, Heidemann RM, Nittka M, Jellus V, Wang J, Kiefer B, Haase A. Generalized autocalibrating partially parallel acquisitions (GRAPPA). Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 2002;47(6):1202-1210.
3. Pruessmann KP, Weiger M, Scheidegger MB, Boesiger P. SENSE: sensitivity encoding for fast MRI. Magnetic Resonance in Medicine: An Official Journal of the International Society for Magnetic Resonance in Medicine 1999;42(5):952-962.
4. Lustig M, Pauly JM. SPIRiT: iterative self‐consistent parallel imaging reconstruction from arbitrary k‐space. Magnetic resonance in medicine 2010;64(2):457-471.
5. Wang S, Su Z, Ying L, Peng X, Zhu S, Liang F, Feng D, Liang D. Accelerating magnetic resonance imaging via deep learning. 2016. IEEE. p 514-517.
6. Lehtinen J, Munkberg J, Hasselgren J, Laine S, Karras T, Aittala M, Aila T. Noise2Noise: Learning image restoration without clean data. arXiv preprint arXiv:180304189 2018.
7. Liu J, Sun Y, Eldeniz C, Gan W, An H, Kamilov US. Rare: Image reconstruction using deep priors learned without groundtruth. IEEE Journal of Selected Topics in Signal Processing 2020;14(6):1088-1099.
8. McCann MT, Jin KH, Unser M. Convolutional neural networks for inverse problems in imaging: A review. IEEE Signal Processing Magazine 2017;34(6):85-95.
9. Lucas A, Iliadis M, Molina R, Katsaggelos AK. Using deep neural networks for inverse problems in imaging: beyond analytical methods. IEEE Signal Processing Magazine 2018;35(1):20-36.
10. Knoll F, Hammernik K, Zhang C, Moeller S, Pock T, Sodickson DK, Akcakaya M. Deep-learning methods for parallel magnetic resonance imaging reconstruction: A survey of the current approaches, trends, and issues. IEEE signal processing magazine 2020;37(1):128-140.
11. Liang D, Cheng J, Ke Z, Ying L. Deep magnetic resonance image reconstruction: Inverse problems meet neural networks. IEEE Signal Processing Magazine 2020;37(1):141-151.
12. Akçakaya M, Moeller S, Weingärtner S, Uğurbil K. Scan‐specific robust artificial‐neural‐networks for k‐space interpolation (RAKI) reconstruction: Database‐free deep learning for fast imaging. Magnetic resonance in medicine 2019;81(1):439-453.
13. Mardani M, Gong E, Cheng JY, Vasanawala SS, Zaharchuk G, Xing L, Pauly JM. Deep generative adversarial neural networks for compressive sensing MRI. IEEE transactions on medical imaging 2018;38(1):167-179.
14. Han Y, Sunwoo L, Ye JC. e deep learning for accelerated MRI. IEEE transactions on medical imaging 2019;39(2):377-386.
15. Liu J, Sun Y, Xu X, Kamilov US. Image restoration using total variation regularized deep image prior. 2019. Ieee. p 7715-7719.
16. Aggarwal HK, Mani MP, Jacob M. MoDL: Model-based deep learning architecture for inverse problems. IEEE transactions on medical imaging 2018;38(2):394-405.
17. Schlemper J, Caballero J, Hajnal JV, Price A, Rueckert D. A deep cascade of convolutional neural networks for MR image reconstruction. 2017. Springer. p 647-658.
18. Yaman B, Hosseini SAH, Moeller S, Ellermann J, Uğurbil K, Akçakaya M. Self-supervised learning of physics-guided reconstruction neural networks without fully sampled reference data. Magn Reson Med. 2020 ;84(6):3172-3191. doi: 10.1002/mrm.28378. Epub 2020 Jul 2. PMID: 32614100; PMCID: PMC7811359.
19. Uecker M, Lai P, Murphy MJ, Virtue P, Elad M, Pauly JM, Vasanawala SS,Lustig M. ESPIRiT--an eigenvalue approach to autocalibrating parallel MRI: where SENSE meets GRAPPA. Magn Reson Med. 2014 Mar;71(3):990-1001. doi: 10.1002/mrm.24751. PMID: 23649942; PMCID: PMC4142121.
20. Zhang, Shuo, Kai Tobias Block, and Jens Frahm. "Magnetic resonance imaging in real time: advances using radial FLASH." Journal of Magnetic Resonance Imaging 31.1 (2010): 101-109
Figures