2923
Improving variational network based 2D MRI reconstruction via feature-space data consistency1The Bernard and Irene Schwartz Center for Biomedical Imaging (CBI), Department of Radiology, New York University Grossman School of Medicine, New York, NY, United States, 2Facebook AI Research, Meta, New York, NY, United States
Synopsis
Keywords: Image Reconstruction, Parallel Imaging, Compressed Sensing, Deep Learning
Deep learning (DL) methods have enabled state-of-the-art reconstructions of magnetic resonance images of highly undersampled acquisitions. The end-to-end variational network (E2E VarNet) is a DL method that can output high quality reconstructions through an unrolled gradient descent algorithm. Nevertheless, the network discards a lot of high-level feature representations of the image to perform data consistency in the image space. Here, we adapted the E2E VarNet architecture to perform the data consistency in a feature space. We trained the proposed network using the fastMRI brain dataset and observed 0.0013 SSIM improvement for eight-fold accelerations.
Introduction
In MRI, parallel imaging (PI) is probably the best example of a breakthrough that successfully transitioned from research to clinical applications1. Deep learning (DL)-based PI methods2 have enabled reconstructions of diagnostically interchangeable images with impressive quality from three to four-fold accelerated acquisitions3. Nevertheless, as we aim for higher acceleration factors to considerably decrease the scan time and increase the patient's comfort in the scanner, the quality of DL approaches naturally degrades4 and novel model architectures are needed5. In this work, we propose a simple improvement to the end-to-end (E2E) variational network4 (VarNet) model, dubbed FeatureVarNet which performs data consistency using a feature space representation of the images leading to better reconstructions of highly undersampled data.Theory and Methods
Convolutional neural networks (CNN) process the input data and extract a high-level feature representation, that is used to return the output. In the E2E VarNet architecture4 and other unrolled optimization-based models5, most of the high-level features are discarded in the last convolutional layers of each cascade to obtain the update of the image or k-space. In the proposed FeatureVarNet we used the unrolled gradient descent algorithm as in the E2E VarNet4, but unlike E2E VarNet, we performed the updates of the gradient descent in a feature space ($$$f$$$), instead of the k-space ($$$k$$$), or image space. In particular, we introduced two CNNs: an encoder ($$$\mathcal{A}$$$), that maps from $$$k$$$ to $$$f$$$ and a decoder ($$$\mathcal{A}'$$$) that mapped from $$$f$$$ to $$$k$$$. The update rule between the cascades of the FeatureVarNet can be summarized as follows:$$ f_{i+1} = f_i - \lambda \mathcal{A} \{ \mathcal{R} \{ ( \mathcal{E}\{ \mathcal{A}' \{ f_i \} - k_0 \} )\odot M \} \} - {\rm UNET}_i(f_i). \quad \quad (1)$$
Here, $$$\mathcal{E}$$$ and $$$\mathcal{R}$$$ denote the expand and reduce operators of the E2E VarNet4. $$$M$$$ is the undersampling mask, $$$\odot$$$ is the Hadamard product, $$$k_0$$$ is the reference k-space, and $$$\lambda$$$ is the gradient descent's learning rate. In this work, we used a convolutional layer to represent both encoders and decoders. $$$\lambda$$$ and the parameters of all $$${\rm UNET}_i$$$, $$$\mathcal{A}$$$, and $$$\mathcal{A}'$$$ are learned from data. The FeatureVarNet (Figure 1) was trained end-to-end on the brain fastMRI training dataset6. $$$M$$$ sampled a fraction of the central part of the k-space along with a subset of higher frequency lines selected uniformly at random so that the overall acceleration factor (accel.) would be $$$4$$$ or $$$8$$$. We performed one training using the entire training dataset (large: $$$4469$$$ brain volumes) and tested on the entire fastMRI test dataset6. We trained both the FeatureVarNet and the E2E VarNet for $$$70$$$k iteration steps using the Adam optimizer with a learning rate of $$$0.0003$$$.
Results
Figure 2 presents the SSIM, peak signal-to-noise ratio (PSNR), and normalized mean square error (NMSE) convergence of the feature and E2E VarNets for the validation fastMRI dataset. The metrics were measured by comparing the entire 3D reconstructed volume of the sample with the corresponding ground truth and computing the volume average over the entire dataset. Figure 3 compares the SSIM, PSNR, and NMSE of the feature and E2E VarNets on the fastMRI test dataset. Example reconstructions for eight-fold accelerations using data from the validation fastMRI dataset are shown in Figure 4, where we noted a small region of interest to aid visual comparison, using a white square box. The E2E VarNet model failed to reconstruct accurately the blood vessels for the FLAIR brain image in the region of interest, while the FeatureVarNet was able to de-noise the input k-space data and preserve the blood vessels with higher accuracy. For the T1 images with contrast, E2E VarNet blurred the blood vessel in the region of interest, while the FeatureVarNet model preserved it. Finally, for the T2 brain image, the FeatureVarNet was able to detect a small physiological detail shown in the white square region, which was missed by the E2E VarNet.Discussion and Conclusions
We presented the novel FeatureVarNet architecture that extends the E2E VarNet model, but applies data consistency in a CNN feature space instead of k-space. The introduction of encoders and decoders in the FeatureVarNet model lead to higher reconstruction accuracy (according to all metrics) for eight-fold undersampling factors because the network did not discard any high-level feature information in contrast to the E2E VarNet model. The qualitative comparison of Figure 4 for eight-fold accelerations validated the superior performance of the FeatureVarNet over the baseline model since it was able to preserve small physiological details, whereas the E2E VarNet blurred or missed them in the reconstructions. FeatureVarNet reached third place in the fastMRI public leaderboard2 despite the fact that it was not trained on the combination of the train and validation fastMRI datasets as the rest of the leaderboard models. Our initial results suggest that unrolled optimizations-based PI reconstructions can benefit from feature space representations.Acknowledgements
This work was supported by NIH R01 EB024536. It was performed under the rubric of the Center for Advanced Imaging Innovation and Research (CAI2R,www.cai2r.net), an NIBIB National Center for Biomedical Imaging and Bioengineering (NIH P41 EB017183).References
- Larkman, David J., and Rita G. Nunes. "Parallel magnetic resonance imaging." Physics in Medicine & Biology 52.7 (2007): R15.
- Knoll, Florian, et al. "Advancing machine learning for MR image reconstruction with an open competition: Overview of the 2019 fastMRI challenge." Magnetic resonance in medicine 84.6 (2020): 3054-3070.
- Hahn, Seok, et al. "Image quality and diagnostic performance of accelerated shoulder MRI with deep learning–based reconstruction." American Journal of Roentgenology 218.3 (2022): 506-516.
- Sriram, Anuroop, et al. "End-to-end variational networks for accelerated MRI reconstruction." International Conference on Medical Image Computing and Computer-Assisted Intervention. Springer, Cham, 2020.
- Wang, Shanshan, et al. "Deep learning for fast MR imaging: a review for learning reconstruction from incomplete k-space data." Biomedical Signal Processing and Control 68 (2021): 102579.
- Zbontar, Jure, et al. "fastMRI: An open dataset and benchmarks for accelerated MRI." arXiv preprint arXiv:1811.08839 (2018).
Figures
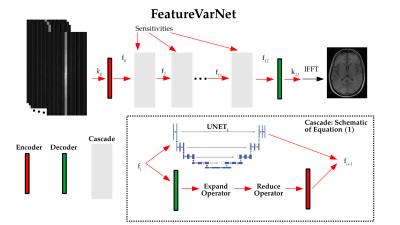

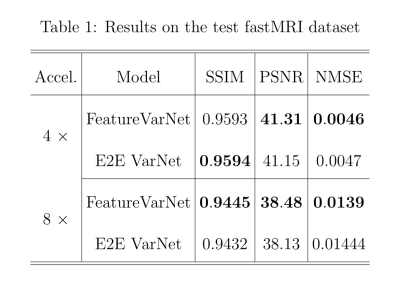
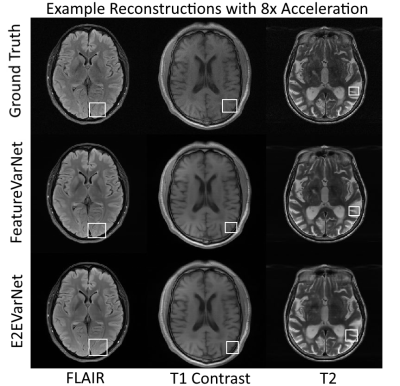
Figure 4: Example brain reconstructions of the validation dataset with the FeatureVarNet and E2E VarNet. The E2E VarNet blurred (FLAIR, T1 contrast) or missed (T2) the physiological details in the noted regions of interest (white square boxes), whereas the featureVarNet was able to preserve them.