2921

Greedy Learning for Memory-Efficient Self-Supervised MRI Reconstruction

Arushi Gupta¹, Batu M Ozturkler², Arda Sahiner², Tolga Ergen², Arjun D Desai^2,3, Shreyas Vasanawala³, John M Pauly², Morteza Mardani², and Mert Pilanci²
¹California Institute of Technology, Pasadena, CA, United States, ²Electrical Engineering, Stanford University, Stanford, CA, United States, ³Radiology, Stanford University, Stanford, CA, United States

Synopsis

Keywords: Image Reconstruction, Image Reconstruction

Deep learning (DL) has recently shown state-of-the-art performance for accelerated MRI reconstruction. However, supervised learning requires fully-sampled training data, and training these networks with end-to-end backpropagation requires significant memory for high-dimensional imaging. These challenges limit the use of DL in high-dimensional settings where access to fully-sampled data is unavailable. Here, we propose self-supervised greedy learning for memory-efficient MRI reconstruction without fully-sampled data. The method divides the end-to-end network into smaller network modules and independently calculates a self-supervised loss for each subnetwork. The proposed method generalizes as well as end-to-end learning without fully-sampled data with at least 7x less memory usage.

Introduction

Deep learning (DL) has shown tremendous success in accelerated MRI reconstruction^1,2, surpassing parallel imaging³ and compressed sensing⁴. However, most DL approaches rely on large amounts of fully-sampled training data. In addition, end-to-end training of DL-based methods require significant GPU memory⁵. Thus, current DL approaches are infeasible for high-dimensional imaging applications such as dynamic-contrast enhanced (DCE) or 4D-flow imaging where it is difficult to acquire fully-sampled training data and the training is constrained by GPU memory due to large data dimensions. Therefore, it is crucial to develop DL-based methods that are memory-efficient and do not require fully-sampled training data for high-dimensional imaging scenarios.
Recently, self-supervised techniques have tackled the dependence on fully-sampled data⁶. However, they rely on deep unrolled models with high memory costs. Although previous methods aim to reduce the memory requirements by using invertible networks ^7,8, deep equilibrium models⁹, or greedy learning¹⁰ for supervised learning, it has not yet been explored whether these approaches can be applied in a self-supervised setting for high-dimensional imaging.
Here, we propose greedy learning for self-supervised MRI reconstruction. Self-supervised greedy learning splits the end-to-end network into several smaller network modules, calculates a self-supervised loss⁶ for each of the sub-network modules and performs independent gradient updates¹⁰. The proposed method removes the requirement for fully-sampled training data, requires at least 7x less GPU memory during training, and achieves similar performance to state-of-the-art methods.

Theory

Model-based deep learning (MoDL) solves the following optimization problem: $$\hat{x} = \underset{x}{\operatorname{argmin}} ||Ax-y||^2_2 + \lambda||x-R(x)||^2$$ where $$$A$$$ is the forward model and $$$R(x)$$$ is the regularization function learned by a convolutional network¹¹.
In end-to-end self-supervised MoDL, a self-supervised loss is calculated at the end of the network. The acquired undersampled k-space indices are split into two disjoint sets: $$$\Psi$$$ and $$$\Lambda$$$. One set of k-space locations, $$$\Psi$$$, is used during training as network inputs, and the second set of k-space locations, $$$\Lambda$$$, serves as pseudo-labels for calculating the loss function⁶. The loss function is given by $$\min_{\theta} \frac{1}{S} \sum_{k=1}^S \mathcal{L}(y_{k,\Lambda}, A_{k,\Lambda}(f_{\theta}(y_{k,\Psi}, A_{k, \Psi})))$$where $$$S$$$ is the number of subjects in the dataset. $$$y_{k,\Psi}$$$ and $$$y_{k, \Lambda}$$$ denote the acquired k-space data for subject $$$k$$$ on the set of k-space locations $$$\Psi$$$ and $$$\Lambda$$$ respectively, $$$f_{\theta}(y_{k,\Psi}, A_{k, \Psi})$$$ denotes the output of the unrolled network for the subsampled k-space data $$$y_{k,\Psi}$$$ and forward model $$$A_{k,\Psi}$$$ of subject $$$k$$$ where the network is parameterized by $$$\theta$$$.
To reduce memory, we apply greedy learning for self-supervised learning of MoDL. In greedy learning, the end-to-end network is split into $$$M$$$ smaller network modules¹⁰. A self-supervised loss is calculated at the end of each network module. Rather than performing a gradient update through the end-to-end network, independent gradient updates are performed for each of the sub-network modules. Since updates are performed independently across different modules, the memory requirement is dependent on the size of each module rather than the entire end-to-end network, decreasing memory usage^10. The proposed algorithm is illustrated in Fig.1.

Methods

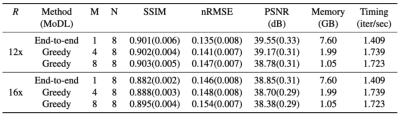
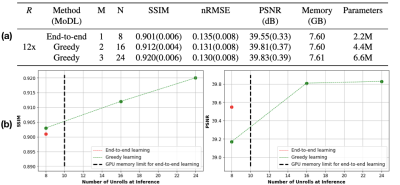
We used a 3D fast-spin echo (FSE) multi-coil knee MRI dataset publicly available on mridata.org¹². The dataset contained unique scans from 19 patients which were split as follows: 14 patients (4480 slices) for training, 2 patients (640 slices) for validation, and 3 patients (960 slices) for testing. Each volume had 320 slices of dimension $$$320 \times 256$$$. Undersampling was performed using a 2D Poisson Disc mask at acceleration rates $$$R = 12,16$$$.

We implemented self-supervised greedy learning and end-to-end self-supervised learning using MoDL¹¹ with a normalized L1-L2 loss, similar to⁶. We first used a network with $$$N = 8$$$ unrolled iterations and trained it with end-to-end learning and greedy learning with $$$M=4,8$$$ greedy blocks at $$$R = 12, 16$$$. Next, we fixed the memory constraint for end-to-end learning and greedy learning, and trained larger networks with greedy learning with $$$N = 16, M = 2$$$, and $$$N = 24$$$, $$$M = 3$$$. Training was performed in PyTorch¹³ using the meddlr repository¹⁴ on a Geforce RTX 2080 GPU (11GB) with batch size 2, and each network was trained for 40000 iterations with Adam¹⁵. We measured reconstruction quality using PSNR, nRMSE and SSIM metrics.

Results

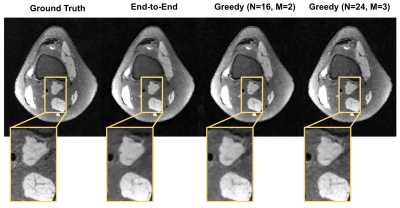
Given the same network architecture, self-supervised greedy learning performed on par with end-to-end learning while using 7.2x less memory with similar iteration timing (Fig.2). Example reconstructions for a knee test slice are shown (Fig.3). Under the same memory constraint, greedy learning allowed for 3x as many unrolled iterations compared to end-to-end learning, which in turn improved reconstruction performance by + 0.019 SSIM, +0.3 dB PSNR, and +0.005 nRMSE (Fig.4). Example reconstructions for a knee test slice demonstrate that greedy learning improves reconstruction fidelity, and mitigates aliasing artifacts, recovering fine anatomical structures (Fig.5).

Discussion and Conclusion

We present self-supervised greedy learning for accelerated MRI reconstruction in high-dimensional imaging applications. Self-supervised greedy learning achieves similar performance to end-to-end self-supervised learning while reducing the memory requirement by at least 7x. Future work will include extending this approach to the DCE and 4D-flow high-dimensional imaging cases where access to fully-sampled data is unavailable.

Acknowledgements

This work was supported by the Caltech Northern California Associates Summer Undergraduate Research Fellowship (SURF) Fellowship, NIH Grants R01 EB009690, R01 EB026136 and NSF Grant DGE-1656518.

References

1. Hammernik K, Klatzer T, Kobler E, et al. Learning a variational network for reconstruction of accelerated MRI data. Magn Reson Med. 2017;79(6):3055-3071. doi:10.1002/mrm.26977

2. Sandino CM, Lai P, Vasanawala SS, Cheng JY. Accelerating cardiac cine MRI using a deep learning‐based ESPIRiT reconstruction. Magn Reson Med. 2021;85(1):152-167. doi:10.1002/mrm.28420

3. M. Murphy, M. Alley, J. Demmel, K. Keutzer, S. Vasanawala, and M. Lustig. Fast ℓ1-SPIRiT compressed sensing parallel imaging MRI: Scalable parallel implementation and clinically feasible runtime. IEEE Trans Med Imaging. 2012;31(6):1250-1262. doi:10.1109/TMI.2012.2188039

4. Lustig M, Donoho D, Pauly JM. Sparse MRI: The application of compressed sensing for rapid MR imaging. Magn Reson Med. 2007;58(6):1182-1195. doi:10.1002/mrm.21391

5. Qin C, Schlemper J, Caballero J, Price AN, Hajnal JV, Rueckert D. Convolutional recurrent neural networks for dynamic MR image reconstruction. IEEE Trans Med Imaging. 2019;38(1):280–290. doi:10.1109/TMI.2018.2863670

6. Yaman B, Hosseini SAH, Moeller S, Ellermann J, Uğurbil K, Akçakaya M. Self-supervised learning of physics-guided reconstruction neural networks without fully sampled reference data. Magn Reson Med. 2020;84(6). doi:10.1002/mrm.28378

7. Kellman, M., Zhang, K., Markley, E., Tamir, J., Bostan, E., Lustig, M., & Waller, L. (2020). Memory-efficient learning for large-scale computational imaging. IEEE Transactions on Computational Imaging, 6, 1403-1414.

8. Wang, K., Kellman, M., Sandino, C. M., Zhang, K., Vasanawala, S. S., Tamir, J. I., ... & Lustig, M. (2021). Memory-efficient Learning for High-Dimensional MRI Reconstruction. arXiv preprint arXiv:2103.04003.

9. Gilton, D., Ongie, G., & Willett, R. (2021). Deep equilibrium architectures for inverse problems in imaging. IEEE Transactions on Computational Imaging, 7, 1123-1133.

10. Ozturkler, B., Sahiner, A., Ergen, T., Desai, A.D., Sandino, C.M., Vasanawala,S., Pauly, J.M., Mardani, M., Pilanci, M. GLEAM: Greedy learning for large-scaleaccelerated mri reconstruction (2022). https://arxiv.org/abs/2207.08393

11. H. K. Aggarwal, M. P. Mani, and M. Jacob, “Modl: Model-based deep learning architecture for inverse problems,” IEEE Transactions on Medical Imaging, vol. 38, no. 2, p. 394–405, Feb 2019.

12. F. Ong, S. Amin, S. Vasanawala, and M. Lustig, “Mridata. org: An open archive for sharing mri raw data,” in Proc. Intl. Soc. Mag. Reson. Med, vol. 26, 2018.

13. Paszke, A., Gross, S., Massa, F., Lerer, A., Bradbury, J., Chanan, G., ... & Chintala, S. (2019). Pytorch: An imperative style, high-performance deep learning library. Advances in neural information processing systems, 32, 8026-8037.

14. Desai, A. D., Gunel, B., Ozturkler, B. M., Beg, H., Vasanawala, S., Hargreaves, B. A., ... & Chaudhari, A. S. (2021). VORTEX: Physics-Driven Data Augmentations for Consistency Training for Robust Accelerated MRI Reconstruction. arXiv preprint arXiv:2111.02549.

15. Kingma, D. P. & Ba, J. (2014), Adam: A Method for Stochastic Optimization arxiv:1412.6980

Figures

Fig.1: The algorithm for MoDL with self-supervised greedy learning. S is number of subjects, $$$M$$$ is the number of greedy blocks. The $$$m$$$^th network module passes inputs $$$x_{k,\Psi}^{(m-1)}$$$ through the current network block, applies conjugate gradient, and calculates a self-supervised loss using the output $$$x_k^{(m)}$$$. A gradient update is then performed and the parameters of greedy block $$$m$$$ are optimized using $$$\min_{\theta_m} \mathcal{L}(y_{k, \Lambda}, A_{k, \Lambda }(x_{k,\Psi}^{(m)}))$$$. This process is repeated until the end of the network.

Fig.2: Comparison of performance, maximum GPU memory during training, and training time for end-to-end self-supervised learning and greedy self-supervised learning with $$$M = 4, 8$$$ greedy blocks with $$$N = 8$$$ unrolled iterations at $$$R = 12,16$$$. Metrics are reported as mean (standard deviation). Greedy learning achieves on par performance while reducing memory with similar iteration time.

Fig.3: Reconstruction of an example knee slice from the 3D FSE multi-coil knee dataset with different reconstruction methods (end-to-end self-supervised learning and greedy self-supervised learning) at $$$R = 12$$$. Greedy learning achieves similar reconstruction quality while reducing memory.

Fig.4: (a) Comparison of performance, number of learnable parameters, and maximum GPU memory during training for end-to-end learning and greedy learning on a single GPU with the same memory. Metrics are reported as mean (standard deviation). (b) SSIM and PSNR with different number of unrolls for greedy learning and end-to-end learning. End-to-end learning reaches its memory limit at $$$N = 10$$$, while greedy learning enables $$$N = 24$$$ to improve performance. While using the same memory, greedy learning enables 3x more unrolls, thereby improving reconstruction quality.

Fig.5: Reconstruction of an example knee slice from the 3D FSE multi-coil knee dataset with different reconstruction methods (end-to-end self-supervised learning and greedy self-supervised learning) on a single GPU with the same memory. As $$$N$$$ increases with greedy learning, the reconstructed images have less blurring, and recover fine anatomical structures.

Proc. Intl. Soc. Mag. Reson. Med. 31 (2023)

2921

DOI: https://doi.org/10.58530/2023/2921